|
| [2096] csábos | 2016-11-18 13:30:19 |
 Általános képlet van erre, de nehezebb mint egy egyszerű formula. Függ a gyöngyök számától is. Ha a gyöngyök számának legnagyobb közös osztója \(\displaystyle n\) akkor a formulában \(\displaystyle d(n)+2\) tag van, ahol \(\displaystyle d(n)\) az \(\displaystyle n\) szám osztóinak számát jelöli.
|
| Előzmény: [2094] epsilon, 2016-11-18 07:07:03 |
|
| [2095] jonas | 2016-11-18 11:33:53 |
 Keressük meg az összes lehetőséget, majd találjuk meg köztük az egyformákat.
Az egyszerűség kedvéért csökkentsük a lehetőségek számát a következőképpen. 3 piros és 5 fehér gyöngyöd van, ezért biztosan van valahol két fehér gyöngy egymás mellett úgy, hogy utána közvetlenül piros gyöngy van. Fűzzük ezért föl a karkötőket először nyitva egy irányított madzagra úgy, hogy a piros gyöngy legyen elől, a két fehér hátul. Csak tíz lehetőség marad (a fehér gyöngyöt jelölje u, a pirosat P):
PPPuuuuu, PPuPuuuu, PPuuPuuu, PPuuuPuu, PuPPuuuu, PuPuPuuu, PuPuuPuu, PuuPPuuu, PuuPuPuu, PuuuPPuu
De ezek között vannak olyanok, amik csak ciklikus eltolásban és esetleg tükrözésben különböznek, ezért gyöngysorként azonosnak kell tekinteni őket. Lehet, hogy ránézésre is meg tudod mondani, hány különböző van. Ha nem, akkor pontosan a következőképpen kell eljárni. Mindegyik nyitott gyöngysorhoz állítsd elő a 16 lehetséges ciklikus eltolását esetleg tükrözve, majd keresd ki ezek közül a lexikografikusan legkisebbet, amit a gyöngysor kanonikus formájának tekinthetünk.
| eredeti | összes ekvivalens | kanonikus |
| PPPuuuuu | {PPPuuuuu, PPuuuuuP, PuuuuuPP, uuuuuPPP, uuuuPPPu, uuuPPPuu, uuPPPuuu, uPPPuuu u, uuuuuPPP, PuuuuuPP, PPuuuuuP, PPPuuuuu, uPPPuuuu, uuPPPuuu, uuuPPPuu, uuuuPPPu} | PPPuuuuu |
| PPuPuuuu | {PPuPuuuu, PuPuuuuP, uPuuuuPP, PuuuuPPu, uuuuPPuP, uuuPPuPu, uuPPuPuu, uPPuPuuu, uuuuPuPP, PuuuuPuP, PPuuuuPu, uPPuuuuP, PuPPuuuu, uPuPPuuu, uuPuPPuu, uuuPuPPu} | PPuPuuuu |
| PPuuPuuu | {PPuuPuuu, PuuPuuuP, uuPuuuPP, uPuuuPPu, PuuuPPuu, uuuPPuuP, uuPPuuPu, uPPuuPuu, uuuPuuPP, PuuuPuuP, PPuuuPuu, uPPuuuPu, uuPPuuuP, PuuPPuuu, uPuuPPuu, uuPuuPPu} | PPuuPuuu |
| PPuuuPuu | {PPuuuPuu, PuuuPuuP, uuuPuuPP, uuPuuPPu, uPuuPPuu, PuuPPuuu, uuPPuuuP, uPPuuuPu, uuPuuuPP, PuuPuuuP, PPuuPuuu, uPPuuPuu, uuPPuuPu, uuuPPuuP, PuuuPPuu, uPuuuPPu} | PPuuPuuu |
| PuPPuuuu | {PuPPuuuu, uPPuuuuP, PPuuuuPu, PuuuuPuP, uuuuPuPP, uuuPuPPu, uuPuPPuu, uPuPPuuu, uuuuPPuP, PuuuuPPu, uPuuuuPP, PuPuuuuP, PPuPuuuu, uPPuPuuu, uuPPuPuu, uuuPPuPu} | PPuPuuuu |
| PuPuPuuu | {PuPuPuuu, uPuPuuuP, PuPuuuPu, uPuuuPuP, PuuuPuPu, uuuPuPuP, uuPuPuPu, uPuPuPuu, uuuPuPuP, PuuuPuPu, uPuuuPuP, PuPuuuPu, uPuPuuuP, PuPuPuuu, uPuPuPuu, uuPuPuPu} | PuPuPuuu |
| PuPuuPuu | {PuPuuPuu, uPuuPuuP, PuuPuuPu, uuPuuPuP, uPuuPuPu, PuuPuPuu, uuPuPuuP, uPuPuuPu, uuPuuPuP, PuuPuuPu, uPuuPuuP, PuPuuPuu, uPuPuuPu, uuPuPuuP, PuuPuPuu, uPuuPuPu} | PuPuuPuu |
| PuuPPuuu | {PuuPPuuu, uuPPuuuP, uPPuuuPu, PPuuuPuu, PuuuPuuP, uuuPuuPP, uuPuuPPu, uPuuPPuu, uuuPPuuP, PuuuPPuu, uPuuuPPu, uuPuuuPP, PuuPuuuP, PPuuPuuu, uPPuuPuu, uuPPuuPu} | PPuuPuuu |
| PuuPuPuu | {PuuPuPuu, uuPuPuuP, uPuPuuPu, PuPuuPuu, uPuuPuuP, PuuPuuPu, uuPuuPuP, uPuuPuPu, uuPuPuuP, PuuPuPuu, uPuuPuPu, uuPuuPuP, PuuPuuPu, uPuuPuuP, PuPuuPuu, uPuPuuPu} | PuPuuPuu |
| PuuuPPuu | {PuuuPPuu, uuuPPuuP, uuPPuuPu, uPPuuPuu, PPuuPuuu, PuuPuuuP, uuPuuuPP, uPuuuPPu, uuPPuuuP, PuuPPuuu, uPuuPPuu, uuPuuPPu, uuuPuuPP, PuuuPuuP, PPuuuPuu, uPPuuuPu} | PPuuPuuu |
Ebből látható, hogy pontosan öt különböző gyöngysor van:
PPPuuuuu, PPuPuuuu, PPuuPuuu, PuPuPuuu, PuPuuPuu
|
| Előzmény: [2094] epsilon, 2016-11-18 07:07:03 |
|
| [2094] epsilon | 2016-11-18 07:07:03 |
 Kedves csábos és Mihály! Köszönöm a válaszokat! Kiderült tehát annyi, hogy a 8-cal való osztás nem helyénvaló. Ok, elmondom, hogyan gondolkodtam: mindenki tudja, hogy n személyt egy kerekasztal körül n!/n= (n-1)! módon lehet elhelyezni, ez az n elem cirkuláris permutációja, az n-el való osztás logikus. A mi esetünkben ismétléses permutációról van szó, aminek a P(m,n)=(m+n)!/m!×n! képletét a nem ismétléses permutációból vezettük le. Ezen tűnődöm, hogy ha a nem ismétléses permutációra a cirkuláris esetben van képlet, akkor miért nincs az ismétléses permutáció esetén is a cirkuláris változatra, legalábbis ezt kerestem, mert sehol sem láttam. Tehát tudna e valaki mondani olyan képletet, ami ismétléses permutációhoz kapcsolódik, és amellyel ezeket a gyöngyös feladatokat meg lehet oldani általános formában, mert biztosan kell létezzen ilyen képlet, megoldás, mert nem lehet az, hogy empirikusan, próbálgatásokkal oldjuk meg az ilyen feladatokat. Üdv: epsilon
|
|
| [2093] Sinobi | 2016-11-18 00:39:43 |
 Mennyire nehéz?
És, hogy célszerű megoldani az 5000 fehér, 3000 piros esetet?
|
|
| [2092] csábos | 2016-11-17 22:22:23 |
 11-es Apáczai könyv?
Képzeld el a 4 piros 4 fehért: \(\displaystyle \frac{8!}{4!4!}\)-t kéne osztni 8-cal. De ez nem egész :-(.
Ez egy nehéz feladat, próbálgatással célszerű megoldani.
|
| Előzmény: [2090] epsilon, 2016-11-17 19:00:11 |
|
|
| [2090] epsilon | 2016-11-17 19:00:11 |
 Üdv mindenkinek! Lenne egy kérdésem, mert nem jutok dűlőre. Van 3 piros és 5 fehér gyöngy. Ezek segítségével hány különböző karkötő fűzhető? Én ismétléses permutációval számoltam ki 8!/3!*5!=56 és mivel a körön akárhol elvágható a karkötő, ezért ezen elvágásokból kifolyólag, 8-al el kell osztani az előbbi eredményt, így 56:8=7 adódik. Ellenben a megoldásnál a könyvben így okoskodnak: A 3 piros gyöngy a karkötőt három ívre bontják: a három ívre ráhelyezzük az 5 fehér gyöngyöt. (forgásszimmertia miatt az ívek egyenrangúak). A fehér gyöngyök száma egyes íveken: 005, 014, 113, 122, 023. Tehát 5 különböző karkötő van. melyik a helyes válasz, az 5 vagy a 7? Hol a másik megoldásban a hiba? Előre is köszönöm, üdv: epsilon
|
|
| [2089] Róbert Gida | 2016-08-21 13:16:57 |
 Az tényleg csoda. Az optimális ugyanis 4 csoport. A felső háromszögmátrix részét használtam a táblázatnak (a program a szimmetrikus részét elkészíti); Glpk-ban van is egy gráfszínezős program az examples mappában ami megoldja ezt a problémát egészértékű programozással, csak annyit tettem hozzá, hogy a színezést is kiíratom: http://pastebin.com/USiCAV5x. A megoldás pedig: http://pastebin.com/XC8g8uAC, először a tárgy (sor)száma, majd a szín száma 1-4-ig. (itt a heurisztikus gyors megoldás is rátalált az opt. megoldásra).
Kicsivel egyszerűbb programmal is meg lehet ezt oldani: rögzítem a színek számát és így keresek egy színezést, ha nincs akkor növelem eggyel a színek számát (ez annyiban kedvezőbb is lehet futásidőben, hogy kevesebb változót használunk). Amúgy nem meglepő ez a fajta megoldás, órarendkészítést tipikusan egészértékű programozással oldunk meg.
|
| Előzmény: [2087] lorantfy, 2016-08-20 22:16:21 |
|
|
| [2087] lorantfy | 2016-08-20 22:16:21 |
 Sikerült 3 csoportba gyűjteni, ami szinte egy csoda!
|
|
| [2086] jonas | 2016-08-18 19:48:34 |
 Ennek a táblázatnak nem kéne szimmetrikusnak lennie? A MAGY E, MAGY K az egyik irányban meg van jelölve, de a másik irányban nincs. Meg tudnád adni a helyes gráfot, és lehetőleg nem csak képként?
|
| Előzmény: [2084] lorantfy, 2016-08-18 15:32:21 |
|
|
| [2084] lorantfy | 2016-08-18 15:32:21 |
 Segítségeteket kérem egy valós problémához, ami azt is mutatja, hogy az órarend összeállítása a mai középiskolákban a lehetetlennel határos. A faktos csoportok láthatók a táblázatban. Az X-ek azt jelentik, hogy van olyan tanuló, aki az oszlop és sor faktot (tantárgyat) együtt választotta. Cél: Minél kevesebb olyan csoportot kell kialakítani a tantárgyakból, amelyek mehetnek egy időben, tehát nincs olyan tanuló, aki egyszerre választotta őket és egyszerre két helyen kéne lennie. Minden ötletet szívesen veszek. Előre is köszönöm!
|
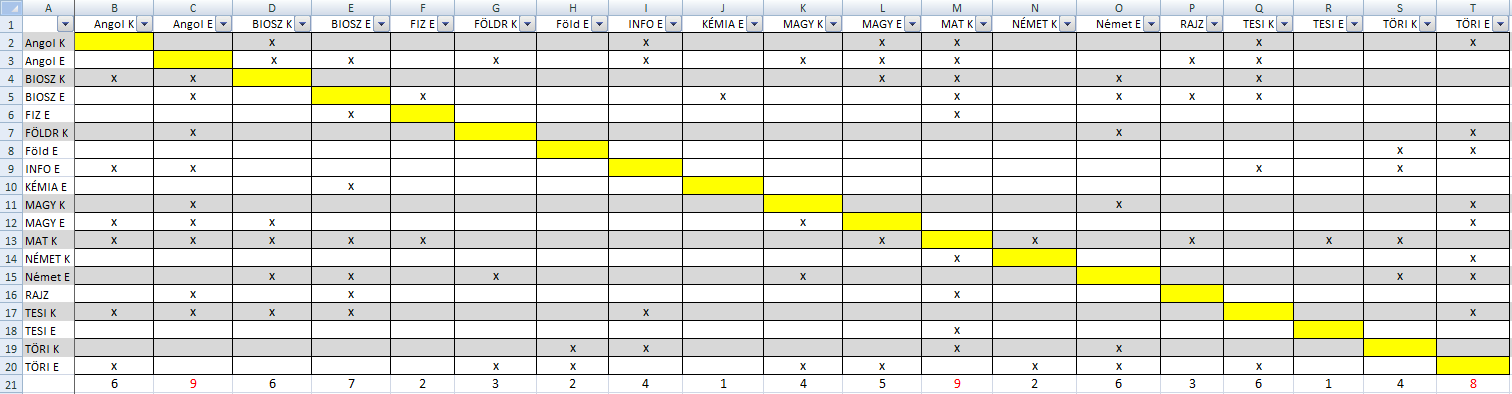 |
|
| [2083] Jhony | 2016-07-31 04:15:10 |
 Üdvözletem - szóval még is csak lenne valaki ,akit érdekelne a téma - nagyon örülök ennek és folytatom az elképzelésem vagyis amit ott az openstudy.com/mathematics oldalon leírtam . - elképzelésem szerint az első alapprím a kettes,az egyedüli páros,majd egy szám különbségre követi a hármas,az első páratlan prím -(itt jegyezném meg,hogy ők,mint egy szám különbségű prímek,lehetnének ,,társ-prímek" - 2 - 3
- az első kör 2 szorozva 3 = 6 +/- 1 = 5 - 7 és így bővül első körben négyre a prímnemzetség
- 5 - 7
- 5 + 7 = 12 +/- 1 = 11 - 13 ikerprímek
- 11 - 13
- 11 + 13 = 24×3=72 +/- 1 = 71 -73 ikerprímek
- 71 - 73
- 71+73=144×3=432 +/- 1 = 431 - 433 ikerprímek
- 431 -433
- 431+433=864×3=2592 +/- 1 = 2591 - 2593 ikerprímek
- és ez lenne az eddigi leghosszabb ikerprím-családfa amit logikusan a kapcsolatok leírásával érthetően értelmezni lehet
köszönöm szépen a véleményeket
|
| Előzmény: [2076] HoA, 2016-05-19 10:09:05 |
|
| [2082] Fálesz Mihály | 2016-05-27 11:59:49 |
 Varázsló barátja, Hű De Morgána azt ajánlotta a törpének, hogy a dobozokat úgy helyezze el, hogy csak egyetlen &tex;\displaystyle L&xet; limeszpontjuk legyen. Újult lelkesedéssel látott munkához; egyhelyben ülve, két kézzel rakosgatta a köveket. Nagyon élvezte, hogy amikor egy követ belerak egy dobozba, a másik kezével már veheti is ki a dobozból a másik követ. A végén újra belenézett a dobozokba, és azok --- ahogy várta --- ismét üresek voltak, viszont az összes követ ott látta az &tex;\displaystyle L&xet; pontban.
--- Én soha nem tettem egy követ sem az &tex;\displaystyle L&xet; pontba! Hogy kerültek mégis oda? --- faggatta Merlint.
--- Oda konvergáltak. Ha a köveket pontszerűnek tekintjük, azt mondhatjuk, hogy minden egyes kő egy-egy folytonos görbén mozgott, és ezeknek a görbéknek a közös limesze a 11 órás időpontban éppen az &tex;\displaystyle L&xet; pont.
A törpe ezt sem igazán értette, de nagyon örült, hogy nem vesztek el a kövei. Boldogan kiáltott:
--- MEGVANNAK A SZÍNES KÖVEIM! MEGNYERTEM A BÖLCSESSÉG KÖVÉT!
--- Na jó, téd lehet a Bölcsesség Köve -- válaszolta Merlin. --- Adj ide nekem egyet a köveid közül.
A törpe széles, diadalmas mosollyal ki akarta nyújtani a kezét, hogy kivegyen egy követ az &tex;\displaystyle L&xet; pontból, de ekkor kellemetlen meglepetés érte.
--- Öööö... hova lettek a kezeim?
--- A kezed részecskéi a klasszikus modell szerint pontszerűek, és folytonos görbéken mozognak, de ez csak egyszerűsített modell. A finomabb kvantummechanikai rendszerben a részecskék helyének valószínűségi eloszlását az állapotfüggvényük írja le. A szokásos esetekben az állapotfüggvény egy kis halmazra koncentrálódik, ezért kezelhetjük a részecskéket pontszerűnek. A te eseted viszont valamivel komplikáltabb. Tetszőleges &tex;\displaystyle \varepsilon>0&xet;-ra igaz, hogy &tex;\displaystyle 11-\varepsilon&xet; és &tex;\displaystyle 11&xet; között te az összes dobozba beledugtad mindkét kezedet. Ezért az állapotfüggvények idő szerinti limesze sokkal nagyobb térrészen, a dobozok körül szóródik szét.
--- Már megint nem értem. Muszáj mindig ilyen tudományos bikkfanyelven fogalmazni?
--- Rendben. A kezeid szétkenődtek a térben egy, a dobozok körüli felhőben.
--- Hú. Akkor vegyél el te magadnak egy színes követ az &tex;\displaystyle L&xet; pontból, és léccí, add ide nekem a Bölcsesség Kövét!
--- A kristály törékeny. Tartok tőle, hogy nem tudnád megfogni, átesne a felhőn...
|
| Előzmény: [2081] Sinobi, 2016-05-26 22:44:00 |
|
| [2081] Sinobi | 2016-05-26 22:44:00 |
 "Amit én hiányolok a meséből, az az, hogy hol volt a törpe a feladat végén. :-)"
A törpe felkereste Merlin ősellenségét, Morgánát, aki azt javasolta a törpének, hogy dél előtt egy fél órával markoljon bele az első dobozba, szedje ki belőle a semmit, rakja vissza a nagy dobozba, és ezt folytassa egészen délig. Csodálkozott a törpe, de végrehajtotta. Végén az összes (egy szám sem hiányzott) köve ott lapult a nagy dobozban, amit még kevésbé értett. Morgána hisztérikus gonosz nevetéséből a "kompakkság" szót vélte kihallani, de arra nem dobott semmit a keresője, belenyugodott.
Merlin nem csak a bölcsek kövét vesztette így el, de kiderült hogy a hulladékmegsemmisítő üzemei sem pont azt csinálják amit szeretne -- ki kellett hát valamit találnia...
Segítsünk Merlinnek! Adjunk olyan algoritmust, amelyik képes a gömbön vagy a projektív síkon* is megsemmisíteni a dolgokat!
* a törpék 0 magasak
|
| Előzmény: [2080] Fálesz Mihály, 2016-05-26 06:49:20 |
|
| [2080] Fálesz Mihály | 2016-05-26 06:49:20 |
 Én úgy értem a kérdést, hogy a második feladatban is a későbbi kő mozog tovább a kisebb sorszámmal, tehát megismételjük az első feladatot; a kövek nem sétálnak ki a végtelenbe, csak a sorszámok. Az &tex;\displaystyle n&xet;-edik lépésben az &tex;\displaystyle n&xet;-edik kő (&tex;\displaystyle 1&xet;-es sorszámmal) bekerül az &tex;\displaystyle n&xet;-edik dobozba, és többször már nem vesszük ki a dobozból, viszont a számát minden menetben letöröljük és &tex;\displaystyle 1&xet;-gyel nagyobbra cseréljük.
A feladat végén minden dobozban egyetlen, számozatlan kő lesz, az &tex;\displaystyle n&xet;-edik dobozban az eredetileg &tex;\displaystyle n&xet;-edik kő.
Amit én hiányolok a meséből, az az, hogy hol volt a törpe a feladat végén. :-)
|
| Előzmény: [2079] csábos, 2016-05-25 22:58:51 |
|
|
| [2078] Sinobi | 2016-05-22 18:11:10 |
 Ki tudja-e úgy cselezni az irigy törpe Merlint, hogy a második feladat végrehajtása során mindig amikor két kő kerülne egy dobozba, akkor (Merlinnek háttal állva, és parányi testével takarva amit csinál) nagyon gyorsan kicserélné a kövek sorszámait?
|
|
| [2077] Lpont | 2016-05-19 11:53:44 |
 "- ezzel kapcsolatban van egy vagyis szerkesztettem egy saját képlet által felállított prím-családfát,amit ott az oldalon megosztottam ideértve a szerkesztéshez,felállításhoz használt teljes útmutatót,leírást -"
Oszd meg velünk is kérlek.
|
| Előzmény: [2071] Jhony, 2016-03-27 13:36:35 |
|
| [2076] HoA | 2016-05-19 10:09:05 |
 Családfáról szólva arra gondol az ember, hogy a benne szereplő elemek - alapértelmezésben emberek - közötti rokonsági kapcsolatokat ábrázoljuk. Hogy értelmezed prímek esetére a fogalmakat? Mikor van két prím szülő-gyerek kapcsolatban, kik testvérek, kik házastársak?
|
| Előzmény: [2071] Jhony, 2016-03-27 13:36:35 |
|
|
| [2074] HoA | 2016-05-18 13:01:08 |
 Pontosítani kéne, mit jelent a szélességgel rendelkező mutató. Ha úgy érted, hogy mindegyik legalább d szélességű, a tengelynél is, akár lekerekítve,akkor az r = d/2 sugarú kis kör minden pontját mindig mindegyik mutató fedi. Vagy keskeny körcikk alakú mutatókra gondolsz, a tengelynél 0 szélességgel?
|
| Előzmény: [2072] Sinobi, 2016-04-10 22:30:58 |
|
| [2073] marcius8 | 2016-05-17 14:28:54 |
 Meg tudja valaki mondani, hogy egy normális (9x9-es) szudoku táblázatot hányféleképpen lehet kitölteni? Tisztelettel: Bertalan Zoltán.
|
|











