Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93]

Szeretnél hozzászólni? Jelentkezz be.

[208] gdoki

2007-06-23 00:26:11

Hi bárki!

Főiskolás volnék és nagyon elhanyagoltam a matekot...most szeretném bepótolni, csak rövid az időm az alábbi feladatra. Válaszokat előre is köszönöm!

[207] farkasroka	2007-06-15 12:06:15
köszönöm a segítséget

[206] Lóczi Lajos

2007-06-13 22:00:21

Legyen x₀ $\ne$ 0 és $\varepsilon$ >0 rögzített. Legyen $\delta$ egyelőre olyan, hogy $\delta$ $\le$ |x₀|/2. Legyen x tetszőleges olyan, hogy |x-x₀|< $\delta$ . A reciprokfüggvény folytonos x₀-ban, mert

$|1/x-1/x_0|=\frac{|x-x_0|}{|x||x_0|}\le \frac{\delta}{|x_0||x_0|/2},$

tehát $\delta$ :=min (|x₀|/2, $\varepsilon$ /2^.x₀²) megfelelő.

Előzmény: [205] farkasroka, 2007-06-13 17:22:43

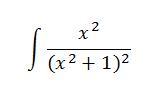[205] farkasroka

2007-06-13 17:22:43

Sziasztok!

Azt szeretném tudni, hogyan lehet az 1/x függvény folytonosságát bizonyítani közvetlenül a definícióból, pontosabban hogyan függ a delta az epszilontól a szokásos jelölésekkel?

Elnézést a triviális kérdésért, segítségeteket előre is köszönöm!

[204] phantom_of_the_opera	2007-05-25 10:53:11
Aha... hát köszönöm szépen a segítséget. Megkíméltél attól, hogy bebizonyítsak egy olyan állítást, ami nem igaz :)
Előzmény: [203] Csimby, 2007-05-23 01:22:00

[203] Csimby	2007-05-23 01:22:00
Z_n az n rendű ciklikus csoport. Z_n×Z_k pedig ezek direkt-szorzata, úgy képzeld el, hogy minden elemnek van két koordinátája és a csoport művelet az elsőkoordinátán Z_n-ből a másodikon Z_k-ból öröklődik. Tehát (a,b) összeműveletezve (c,d)-vel egyenlő (a+c,b+d)-vel ahol a-t és c-t Z_n-ben adtuk össze, b-t és d-t pedig Z_k-ban. Könnyen látható hogy ez csoport és rendje nk. (Z_n-re gondolhatunk úgy mint a modulo n maradékosztályokra az összeadásra nézve, és mivel Abel-csoport, ezért írtam "+"-val a műveletet, ekkor az egység elem a 0, a generátor elem (ami önmagával összeműveletezve kiadja az egész csoportot) pedig az 1). Már csak azt kell meggondolni, hogy Z₂₇×Z₃-ban (1,0) rendje tényleg 27, vagyis (1,0)+...+(1,0) (27-szer összeadva) tényleg egyenlő (0,0)-val. És hogy Z₂₇×Z₃ nem ciklikus (vigyázat pl. Z₄×Z₃ ciklikus). De mondjuk más ellenpélda is lehetséges, mivel g²⁹=g² akkor is teljesül pl. ha g³=1 vagy g⁹=1. Vagy esetleg g maga az egységelem.
Előzmény: [202] phantom_of_the_opera, 2007-05-22 22:40:03

[202] phantom_of_the_opera	2007-05-22 22:40:03
Hmm. Ha ez így igaz (egyelőre nem látom át), akkor megint a feladat a rossz?? A 192-es hozzászólásomban szereplőről is kiderült utólag, hogy úgy ahogy le van írva, nincs értelme...
Előzmény: [201] Csimby, 2007-05-22 22:18:03

[201] Csimby	2007-05-22 22:18:03
g²⁹=g²-ből g²⁷=1. A 81 rendű csoport lehet akár Z₂₇×Z₃, amiben van 27-rendű elem pl. (1,0) ahol 1 Z₂₇ generátoreleme, 0 pedig Z₃ egységeleme. De ez a csoport nem ciklikus. Remélem nem írtam hülyeséget.
Előzmény: [200] phantom_of_the_opera, 2007-05-22 11:18:59

[200] phantom_of_the_opera

2007-05-22 11:18:59

Sziasztok!

Egy csoportelméleti kérdésem lenne, amennyiben valaki tud segíteni. Azt kellene bebizonyítanom, hogy ha egy 81 rendű csoportban van olyan elem, amelyre g²⁹=g², akkor a csoport ciklikus. A gond az, hogy nem sikerül...

Előre is köszi.

[199] V Laci	2007-04-17 17:38:00
Köszönöm szépen!

[198] SAMBUCA	2007-04-17 00:19:09
Na igen, én is itt találtam: 8³=64³+23³+42³+421³. :)
Előzmény: [196] V Laci, 2007-04-16 14:29:56

[197] Lóczi Lajos

2007-04-17 00:06:51

http://mathworld.wolfram.com/HadwigerProblem.html

http://mathworld.wolfram.com/CubeDissection.html

Ezek megmondják, hogy az Amer. Math. Monthly melyik számában van meg a megoldás, a könyvtárban tehát utánanézhetsz szükség esetén.

Előzmény: [196] V Laci, 2007-04-16 14:29:56

[196] V Laci

2007-04-16 14:29:56

Szia!

Igen, tényleg ezt szeretném bizonyítani. A többi maradékra már megvan a szerintem legkisebb konstrukció, azonban az 5-ös maradékra a legkisebb, amit elő tudtam állítani, az a 61 kockás darabolás. És szeretnék lejjebb menni. :)

Előzmény: [195] Sirpi, 2007-04-16 13:38:38

[195] Sirpi

2007-04-16 13:38:38

Szia!

Fel tudtam valaha, egyszer már végigküzdöttem ezt. Gondolom azt akarod bizonyítani, hogy ha n>47, akkor egy kocka felosztható n kisebb kockára, és ebből tényleg a legnehezebb lépés az n=54 eset megoldása. Ugye ha összevonunk 8 egybevágó kockát egy kétszer akkorává, akkor a darabszám 7-tel csökken, vagyis ilyen lépések során a 7-es maradék nem változik. Éppen ezért elég minden 7-es maradékú n-re megoldani a felosztást, ugyanabban a maradékosztályban a nagyobbakra automatikusan adódik.

A nagy kockánál ez a maradék 1, viszont nekünk az 5-ös maradékot kell megcéloznunk, tehát 4-gyel kell növelni. Egy kocka 3x3x3-má vágása 2-vel csökkenti a 7-es maradékot, ugyanígy 3x3x3 összeforrasztása meg 2-vel növeli. Régen is így csináltam valahogy, de most még nem látom még pontosan, hogy hogy is volt a tényleges felosztás, de hátha ez alapján valaki más gyorsan megcsinálja :-)

Előzmény: [194] V Laci, 2007-04-16 13:08:16

[194] V Laci	2007-04-16 13:08:16
Sziasztok! Fel lehet-e darabolni egy kockát 54 kiskockára? Ha igen, hogyan? Előre is köszönöm!

[193] HoA	2007-04-12 15:02:16
1/7 tizedestört alakban = 0,142857142857142857142857142857... , vagyis a jegyek 6-osával ismétlődnek. 2004 osztható 6-tal ( 3-mal osztható és páros ) , tehát a 2005-ik jegy a ciklus első jegye, vagyis 1.
Előzmény: [190] hajnalkalive, 2007-04-11 18:32:35

[192] phantom_of_the_opera	2007-04-11 23:22:44
Sziasztok! Gráfos feladattal kapcsolatban kérnék segítséget: Bizonyítsuk be, hogy ha egy n pontú egyszerű gráf leghosszabb útja két végpontjának fokszámösszege legalább n, akkor a leghosszabb utak között van 2, amelyek végpontjai szomszédosak. Előre is köszönöm.

[191] jonas	2007-04-11 20:28:32
A téglalap átlója a hosszabbik oldallal $\alpha$ /2 szöget zár be, ezért aztán a hosszabbik oldal hossza dcos ( $\alpha$ /2), a rövidebbik oldalé dsin ( $\alpha$ /2). Ebből a téglalap kerülete 2d(sin ( $\alpha$ /2)+cos ( $\alpha$ /2))= $2\sqrt2 d\sin(\alpha/2 + \pi/4)$ vagy valami hasonló. A terület d²cos ( $\alpha$ /2)sin ( $\alpha$ /2)= d²/2^.sin $\alpha$ .
Előzmény: [190] hajnalkalive, 2007-04-11 18:32:35

[190] hajnalkalive

2007-04-11 18:32:35

Tud segíteni valaki?

Mennyi 2005 számjegy a tizedesvessző után 1/7 tizedestört alakban?

Egy téglalp átlói d cm hosszúak, az átlók által bezárt hegyesszög alfa fok. Fejezzük ki a téglalp területét és kerületét d-vel és alfával.

[189] pvong17	2007-04-11 18:06:00
Köszönöm.

[188] Lóczi Lajos

2007-04-10 23:39:52

Reggelre kell? :)

Biztos leírtunk egy ilyet már itt: Pitagorasz-tétel a jobboldali tag kitevőjében (cos²(x)=1-sin²(x)), új ismeretlen (A:=4^sin²(x)) és másodfokú egyenlet.

4^sin²(x)+4^1-sin²(x)=4, azaz A+4/A=4, vagyis A_1,2=2, tehát $|\sin(x)|=1/\sqrt{2}$ , ezt meg kitalálod.

Előzmény: [187] pvong17, 2007-04-10 23:16:19

[187] pvong17

2007-04-10 23:16:19

Üdvözlet mindenkinek!

Jó lenne a segítene valaki ebben , már nem nagyon tudok sehová fordulni:

4^sin²x + 4^cos²x = 4

[186] nadorp

2007-03-30 19:07:42

Sorry,de ezt alaposan elszámoltam. Helyesen a kérdéses S_n összegre elég nagy n esetén

$-1-\epsilon\leq{S_n}-(2\sqrt{n}-\frac\pi2)\leq\epsilon$

Előzmény: [184] nadorp, 2007-03-30 13:45:25

[185] Willy	2007-03-30 16:50:25
Szeretnék egy egyszerű modellt kreálni a globális felmelegedés modellezésére, de honnét lehetne megbízható adatokat szerezni? (Pl.: CO₂ mennyire fogja vissza a meleget... ezt a molekula méretéből is meg lehet-e mondani?)

[184] nadorp	2007-03-30 13:45:25
Ha az összeget az $\int{arc}\tan{\frac1{\sqrt{x}}}dx$ integrállal alulról és felülről becsüljük ( felülről 0-tól n-ig, alulról 1-től n+1-ig ), akkor az összeg a $2\sqrt{n}-ln(1+\sqrt{n})$ értékétől kb. 1-re van.
Előzmény: [182] Lóczi Lajos, 2007-03-30 00:16:13

Már regisztráltál?
Új vendég vagy?