| [2114] jonas | 2017-01-25 22:17:44 |
 Próbáld meg a \(\displaystyle 3x2y+3xy2 \) kifejezést szorzattá alakítani úgy, hogy minden tényező az \(\displaystyle x \) és \(\displaystyle y \) változók egész együtthatós polinomja maradjon. Ha egész megoldásokat keresel, akkor ezeknek a tényezőknek az értéke is egész lesz, így mindegyiknek az értéke a \(\displaystyle 216 \) szám osztója. Ennek a számnak csak 32 osztója van, ezért így nagyon le tudod szűkíteni a lehetőségeket.
|
| Előzmény: [2113] Niels Bohr, 2017-01-24 19:28:35 |
|
| [2113] Niels Bohr | 2017-01-24 19:28:35 |
 Sziasztok!
Szeretnék egy kis segítséget kérni a
\(\displaystyle 216=6^{3}=3x^{2}y+3xy^{2}\)
egyenlet egész megoldásainak megtalálásához. Grafikonról leolvastam
az \(\displaystyle x_1=1\), \(\displaystyle y_1=8\) illetve az \(\displaystyle x_2=8\), \(\displaystyle y_2=1\) egész megoldásokat.
Lenne olyan eljárás, amivel az egész megoldásokat megkaphatnám?
Hasonlóan, mint a sokkal egyszerűbb \(\displaystyle y=1/x\) esetén.
|
|
| [2112] HoA | 2016-11-29 10:09:31 |
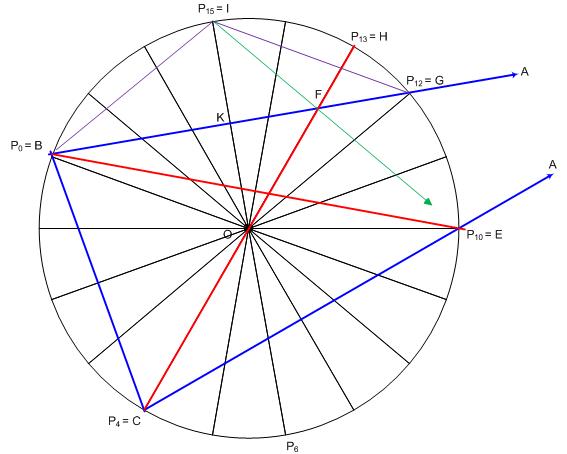
 Talán megér egy ábrát a szabályos 18-szög alapú megoldás, mert a szokásos megközelítés - háromszög körülírt köre = 18-szög körülírt köre - nem túl célravezető.
Legyenek a szabályos 18-szög csúcsai \(\displaystyle P_0 … P_{17}\) , körülírt köre k, középpontja O. Helyezzük el háromszügünket úgy, hogy \(\displaystyle B = P_0\) és \(\displaystyle C = P_4\) legyen . k-ban a kisebb \(\displaystyle P_4 P_{12}\) ívhez tartozik 80 fokos kerületi szög, így a BA egyenes áthalad \(\displaystyle G= P_{12}\) -n. Hasonlóan a CA egyenes átmegy \(\displaystyle P_{10}\) -en. A kisebb \(\displaystyle P_4 P_{10}\) ívhez éppen 60 fokos kerületi szög tartozik, tehát \(\displaystyle E = P_{10}\). Mivel a \(\displaystyle P_{13} P_0\) ívhez tartozik 50 fokos kerületi szög, a CB-vel 50 fokos szöget bezáró egyenes a \(\displaystyle P_4 P_{13} = CH\) átmérő, ennek metszéspontja AB-vel F. A \(\displaystyle P_{12} P_{15} = GI\) és a \(\displaystyle P_{15} P_0 = IB\) ívekhez 60 fokos középponti szög tartozik, OGI és IBO szabályos háromszögek, OGIB rombusz, középpontja legyen K. \(\displaystyle FOK \angle = HOI \angle = P_{13} O P_{15} \angle = 40^o \). IKF és OKF egybevágó derékszögű \(\displaystyle \Delta\)-ek, IF egyenes OF = CF tükörképe AB-re . \(\displaystyle KIF \angle = OIF \angle = P_{6}IF \angle = 40^o\). 40 fokos kerületi szög éppen a \(\displaystyle P_6 P_{10}\) ívhez tartozik, IF tehát átmegy \(\displaystyle P_{10}\) -en , ez feladatunk EF egyenese. A keresett \(\displaystyle x = FEB \angle = IEB \angle = P_{15} P_{10} P_0 \angle = 30^o\).
|
 |
| Előzmény: [2103] w, 2016-11-18 23:02:11 |
|
| [2111] nagyapa | 2016-11-27 22:18:28 |
 geogebra téma: Lineáris fv. ábrázolása (y=mx+b).Minden rendben lenne az m és b csúszkákkal változtathatók. De nem tudom a meredekségi háromszöget beszerkeszteni. Elvileg a fv.görbére egyenest kellene rendelni és a meredekség paranccsal meg kell jelenni a kis háromszögnek.Minden próbálkozásomat szintaktikai hibával dobja vissza. Kérek segítséget.Mi az a 2-3 lépés amivel tovább tudok menni? Közben azt is tapasztaltam, hogy a függvényre tett egyenes leállítja a változtatási lehetőséget.köszönöm.nagyapa.
|
|
|
| [2109] epsilon | 2016-11-22 08:46:46 |
 Ez ugyancsak a sinx/siny=sin30∘/sin110∘ összefüggéshez vezet.
|
|
|
| [2107] csábos | 2016-11-19 18:11:07 |
 Burnside-lemma egy permutációcsoportban. Az orbitok száma megegyezik a fixpontok átlagos számával. A képlet a gyöngyfűzéseket az \(\displaystyle N\)-szög szimmetriái szerint sorolja fel, összeadja azok fixpontjait, és utána átlagolja \(\displaystyle 2N\)-nel. Az \(\displaystyle A\) szám a tükrözések általi fixpontokat jelzi. Nyilván, ha van legalább két páratlan számú szín, akkor nincs tükörszimmetrikus gyöngyfűzés, stb.
|
| Előzmény: [2105] epsilon, 2016-11-19 17:35:37 |
|
| [2106] epsilon | 2016-11-19 17:38:24 |
 Köszi w, azt hittem, hogy erre az eleminek tűnő feladatnak épp olyan elemi megoldása van, mint amilyennek tűnik, mert a sinx/siny= sina/sinb ha x+y= a+b alapján x=a és y=b következik, nehezebbnek tűnik bizonyítani mint az eredeti feladat.
|
| Előzmény: [2103] w, 2016-11-18 23:02:11 |
|
| [2105] epsilon | 2016-11-19 17:35:37 |
 Hát ez igen Csábos! Erre nem számítottam, hiszen én mind azt hittem, hogy az ismétléses permutáció képletéből kiindulva, valahogyan le lehet vezetni az általánosabb esetet bár két színű golyóra, de ezek a képletek nagyon jól tükrözik a feladat általánosításának a komplexitását. valami szakirodalmi forrásanyagot tudsz-e adni, ahol ezzel az általános problémával foglalkoznak?
|
| Előzmény: [2104] csábos, 2016-11-19 17:10:11 |
|
| [2104] csábos | 2016-11-19 17:10:11 |
 Íme a képlet
Legyen \(\displaystyle g_1, g_2, ..., g_k\) a különböző színű gyöngyök száma
\(\displaystyle N = \sum_{i=1}^{i=k}{g_i}\)
\(\displaystyle \text{ Nyakláncok száma}=(A+B)/2N\)
Ahol
- ha 2-nél több páratlan darabszámú szín van: A=0
- ha 2 páratlan darabszámú szín van:
\(\displaystyle A =\frac{((N/2)-1)!}{\prod_{i=1}^{i=k}(\left\lfloor g_i/2\right\rfloor)!}\cdot N\)
- ha 0 vagy 1 páratlan darabszámú szín van:
\(\displaystyle A =\frac{(N/2)!}{\prod_{i=1}^{i=k}(\left\lfloor g_i/2\right\rfloor)!}\cdot N\)
Legyenek \(\displaystyle d\) a \(\displaystyle g_1, g_2, ..., g_k\)-k legnagyobb közös osztójának osztói
\(\displaystyle B=\sum_{j|d}\frac{(N/j)!}{\prod_{i=1}^{i=k}(g_i/j)!}\cdot \varphi(j)\)
|
| Előzmény: [2093] Sinobi, 2016-11-18 00:39:43 |
|
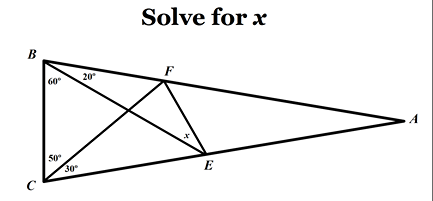
| [2103] w | 2016-11-18 23:02:11 |
 Az adatok mindenképpen elegendőek, mert a megadott szögek hasonlóság erejéig meghatározzák az ábrát.
Ilyen feladatoknál mindig szokott lenni
(1.) valami kedves kreatív szerkesztés, ami a szög megsejtése után nagyon elemi megfontolásokkal vezeti le annak nagyságát (sokszor pakolnak valahova szabályos háromszöget, vagy használják, hogy egy háromszög szögfelezői egy ponton mennek át),
(2.) egy szabályos \(\displaystyle 18\)-szög, aminek néhány átlójának egy ponton való áthaladásával ekvivalens a feladat.
A legegyszerűbb és legkönnyebb módszer azonban (3.) a szinuszarányokkal való számolás szokott lenni. A következő képletet használjuk: ha \(\displaystyle ABC\) háromszögben \(\displaystyle D\) egy pont a \(\displaystyle BC\) oldal belsejében, akkor
\(\displaystyle
\frac{BD}{DC}=\frac{AB}{AC}\cdot \frac{\sin BAD\angle}{\sin DAC\angle}.
\)
Ez a képlet az \(\displaystyle ABD\triangle\) és \(\displaystyle ACD\triangle\) szinusztételeinek leosztásából adódik.
A feladat megoldása. Mivel \(\displaystyle BAC\angle = 20^\circ\), ezért \(\displaystyle EB=EA\), ahonnan \(\displaystyle BEF\angle=x\) és \(\displaystyle FEA\angle=y\) esetén \(\displaystyle x+y=140^\circ\), továbbá
\(\displaystyle
\frac{BF}{FA}=\frac{EB}{EA}\cdot \frac{\sin BEF\angle}{\sin FEA\angle}=\frac{\sin x}{\sin y}
\)
és a szinusztétel szerint
\(\displaystyle
\frac{BF}{FA}=\frac{CB}{CA}\cdot \frac{\sin BCF\angle}{\sin FCA\angle}=\frac{\sin 20^\circ}{\sin 80^\circ}\cdot \frac{\sin 50^\circ}{\sin 30^\circ}=\frac{\sin 20^\circ\cos 40^\circ}{4\sin 20^\circ\cos 20^\circ\cos40^\circ\cdot \frac 12}=\frac{1/2}{\cos 20^\circ}=\frac{\sin 30^\circ}{\sin 110^\circ}.
\)
Tehát
\(\displaystyle
\frac{\sin x}{\sin y}=\frac{\sin 30^\circ}{\sin 110^\circ}.
\)
Ebből \(\displaystyle x+y=140^\circ\) miatt \(\displaystyle x=30^\circ\), \(\displaystyle y=110^\circ\) következik.
//Ugyanis \(\displaystyle x+y=140^\circ\) feltételt rögzítve, \(\displaystyle x\) növelésével, \(\displaystyle y\) csökkentésével \(\displaystyle \frac{\sin x}{\sin y}\) is növekszik. Ezt úgy láthatjuk, ha felveszünk egy \(\displaystyle AOB\angle=140^\circ\)-os szögtartományban egy \(\displaystyle P\) pontot az \(\displaystyle AB\) szakaszon; ekkor \(\displaystyle \frac{\sin x}{\sin y}=\frac{d(P,AO)}{d(P,BO)}\), ha \(\displaystyle PO\) az \(\displaystyle AO\)-val és \(\displaystyle BO\)-val rendre \(\displaystyle x,y\) szöget zár be. Ha \(\displaystyle x\) nő és \(\displaystyle y\) csökken, \(\displaystyle d(P,AO)\) nő és \(\displaystyle d(P,BO)\) csökken, így az arány nő.//
|
| Előzmény: [2100] epsilon, 2016-11-18 17:46:19 |
|
| [2102] csábos | 2016-11-18 21:29:45 |
 Itt a képlet arra, ha 6 narancssárga, 12 kék és 18 zöld gyöngy van. A legnagyobb közös osztó 6. A tagok a 18 szög azon szimmetriáinak felelnek meg, amelyek rendje 6 osztója, 6 a lnko. A kombinatorikus tag együtthatója minden \(\displaystyle d\) osztóra \(\displaystyle \varphi(d)\). A 36-os együttható a tükrözéseknek felel meg. Így valóban csak \(\displaystyle d(n)+1 \) tag van.
\(\displaystyle
\frac{
\binom{36}{18}\cdot\binom{18}{12} +\binom{18}{9}\cdot\binom{9}{6} +
36\cdot \binom{18}{9}\cdot\binom{9}{6} +
2 \cdot \binom{6}{3}\cdot\binom{3}{2} +
2 \cdot \binom{12}{6}\cdot\binom{6}{4}
}{72}
= \\
\frac{\frac{36!}{6!\cdot 12!\cdot 18!} +
37\cdot \frac{18!}{9!\cdot 6!\cdot 3!} +
2 \cdot \frac{6!}{3!\cdot 2!} +
2 \cdot \frac{12!}{6!\cdot 4!\cdot 2!}}{72}
= \\
\frac{168\,470\,811\,709\,200 + 37\cdot4\,084\,080 + 2\cdot13\,860 + 2\cdot60}{72}
= \\
2\,339\,874\,484\,000
\)
|
| Előzmény: [2101] csábos, 2016-11-18 20:51:31 |
|
| [2101] csábos | 2016-11-18 20:51:31 |
 Ehhez meg kell számolni a különböző szimmetriák fixpontjait és beszorozni egy kombinatorikusan kapott együtthatóval. Itt tükrözések, forgatások és identitás jön szóba. Találtam a neten egy példát
http://m.cdn.blog.hu/kr/krisztikt/image/altalam_keszitett.pdf
26.oldal
|
| Előzmény: [2097] epsilon, 2016-11-18 17:16:05 |
|
| [2100] epsilon | 2016-11-18 17:46:19 |
 Közben itt egy másik feladat, mértan, mind körben forgok vele, mintha nem lennének elegendők az adatok, van e valami tippetek:
|
 |
|
| [2099] epsilon | 2016-11-18 17:20:46 |
 Igen Sinobi, Én is kíváncsi lennék ennek a változatnak a megoldására, mert itt nem lehet állítani, hogy látszik, meg stb. Ezért várok egy olyan megoldást, ami általában is érvényes, ilyen nagy számokra is, amit írtál.
|
| Előzmény: [2093] Sinobi, 2016-11-18 00:39:43 |
|
| [2098] epsilon | 2016-11-18 17:18:19 |
 Kedves jónás, becsülöm és csodálom a türelmedet, hogy a sok esetet végig elemezted, de szerintem ez túl nyűgös megoldás. Én egy ismétléses permutációkkal történő megoldásra vadászok.
|
| Előzmény: [2095] jonas, 2016-11-18 11:33:53 |
|
|
| [2096] csábos | 2016-11-18 13:30:19 |
 Általános képlet van erre, de nehezebb mint egy egyszerű formula. Függ a gyöngyök számától is. Ha a gyöngyök számának legnagyobb közös osztója \(\displaystyle n\) akkor a formulában \(\displaystyle d(n)+2\) tag van, ahol \(\displaystyle d(n)\) az \(\displaystyle n\) szám osztóinak számát jelöli.
|
| Előzmény: [2094] epsilon, 2016-11-18 07:07:03 |
|
| [2095] jonas | 2016-11-18 11:33:53 |
 Keressük meg az összes lehetőséget, majd találjuk meg köztük az egyformákat.
Az egyszerűség kedvéért csökkentsük a lehetőségek számát a következőképpen. 3 piros és 5 fehér gyöngyöd van, ezért biztosan van valahol két fehér gyöngy egymás mellett úgy, hogy utána közvetlenül piros gyöngy van. Fűzzük ezért föl a karkötőket először nyitva egy irányított madzagra úgy, hogy a piros gyöngy legyen elől, a két fehér hátul. Csak tíz lehetőség marad (a fehér gyöngyöt jelölje u, a pirosat P):
PPPuuuuu, PPuPuuuu, PPuuPuuu, PPuuuPuu, PuPPuuuu, PuPuPuuu, PuPuuPuu, PuuPPuuu, PuuPuPuu, PuuuPPuu
De ezek között vannak olyanok, amik csak ciklikus eltolásban és esetleg tükrözésben különböznek, ezért gyöngysorként azonosnak kell tekinteni őket. Lehet, hogy ránézésre is meg tudod mondani, hány különböző van. Ha nem, akkor pontosan a következőképpen kell eljárni. Mindegyik nyitott gyöngysorhoz állítsd elő a 16 lehetséges ciklikus eltolását esetleg tükrözve, majd keresd ki ezek közül a lexikografikusan legkisebbet, amit a gyöngysor kanonikus formájának tekinthetünk.
| eredeti | összes ekvivalens | kanonikus |
| PPPuuuuu | {PPPuuuuu, PPuuuuuP, PuuuuuPP, uuuuuPPP, uuuuPPPu, uuuPPPuu, uuPPPuuu, uPPPuuu u, uuuuuPPP, PuuuuuPP, PPuuuuuP, PPPuuuuu, uPPPuuuu, uuPPPuuu, uuuPPPuu, uuuuPPPu} | PPPuuuuu |
| PPuPuuuu | {PPuPuuuu, PuPuuuuP, uPuuuuPP, PuuuuPPu, uuuuPPuP, uuuPPuPu, uuPPuPuu, uPPuPuuu, uuuuPuPP, PuuuuPuP, PPuuuuPu, uPPuuuuP, PuPPuuuu, uPuPPuuu, uuPuPPuu, uuuPuPPu} | PPuPuuuu |
| PPuuPuuu | {PPuuPuuu, PuuPuuuP, uuPuuuPP, uPuuuPPu, PuuuPPuu, uuuPPuuP, uuPPuuPu, uPPuuPuu, uuuPuuPP, PuuuPuuP, PPuuuPuu, uPPuuuPu, uuPPuuuP, PuuPPuuu, uPuuPPuu, uuPuuPPu} | PPuuPuuu |
| PPuuuPuu | {PPuuuPuu, PuuuPuuP, uuuPuuPP, uuPuuPPu, uPuuPPuu, PuuPPuuu, uuPPuuuP, uPPuuuPu, uuPuuuPP, PuuPuuuP, PPuuPuuu, uPPuuPuu, uuPPuuPu, uuuPPuuP, PuuuPPuu, uPuuuPPu} | PPuuPuuu |
| PuPPuuuu | {PuPPuuuu, uPPuuuuP, PPuuuuPu, PuuuuPuP, uuuuPuPP, uuuPuPPu, uuPuPPuu, uPuPPuuu, uuuuPPuP, PuuuuPPu, uPuuuuPP, PuPuuuuP, PPuPuuuu, uPPuPuuu, uuPPuPuu, uuuPPuPu} | PPuPuuuu |
| PuPuPuuu | {PuPuPuuu, uPuPuuuP, PuPuuuPu, uPuuuPuP, PuuuPuPu, uuuPuPuP, uuPuPuPu, uPuPuPuu, uuuPuPuP, PuuuPuPu, uPuuuPuP, PuPuuuPu, uPuPuuuP, PuPuPuuu, uPuPuPuu, uuPuPuPu} | PuPuPuuu |
| PuPuuPuu | {PuPuuPuu, uPuuPuuP, PuuPuuPu, uuPuuPuP, uPuuPuPu, PuuPuPuu, uuPuPuuP, uPuPuuPu, uuPuuPuP, PuuPuuPu, uPuuPuuP, PuPuuPuu, uPuPuuPu, uuPuPuuP, PuuPuPuu, uPuuPuPu} | PuPuuPuu |
| PuuPPuuu | {PuuPPuuu, uuPPuuuP, uPPuuuPu, PPuuuPuu, PuuuPuuP, uuuPuuPP, uuPuuPPu, uPuuPPuu, uuuPPuuP, PuuuPPuu, uPuuuPPu, uuPuuuPP, PuuPuuuP, PPuuPuuu, uPPuuPuu, uuPPuuPu} | PPuuPuuu |
| PuuPuPuu | {PuuPuPuu, uuPuPuuP, uPuPuuPu, PuPuuPuu, uPuuPuuP, PuuPuuPu, uuPuuPuP, uPuuPuPu, uuPuPuuP, PuuPuPuu, uPuuPuPu, uuPuuPuP, PuuPuuPu, uPuuPuuP, PuPuuPuu, uPuPuuPu} | PuPuuPuu |
| PuuuPPuu | {PuuuPPuu, uuuPPuuP, uuPPuuPu, uPPuuPuu, PPuuPuuu, PuuPuuuP, uuPuuuPP, uPuuuPPu, uuPPuuuP, PuuPPuuu, uPuuPPuu, uuPuuPPu, uuuPuuPP, PuuuPuuP, PPuuuPuu, uPPuuuPu} | PPuuPuuu |
Ebből látható, hogy pontosan öt különböző gyöngysor van:
PPPuuuuu, PPuPuuuu, PPuuPuuu, PuPuPuuu, PuPuuPuu
|
| Előzmény: [2094] epsilon, 2016-11-18 07:07:03 |
|
| [2094] epsilon | 2016-11-18 07:07:03 |
 Kedves csábos és Mihály! Köszönöm a válaszokat! Kiderült tehát annyi, hogy a 8-cal való osztás nem helyénvaló. Ok, elmondom, hogyan gondolkodtam: mindenki tudja, hogy n személyt egy kerekasztal körül n!/n= (n-1)! módon lehet elhelyezni, ez az n elem cirkuláris permutációja, az n-el való osztás logikus. A mi esetünkben ismétléses permutációról van szó, aminek a P(m,n)=(m+n)!/m!×n! képletét a nem ismétléses permutációból vezettük le. Ezen tűnődöm, hogy ha a nem ismétléses permutációra a cirkuláris esetben van képlet, akkor miért nincs az ismétléses permutáció esetén is a cirkuláris változatra, legalábbis ezt kerestem, mert sehol sem láttam. Tehát tudna e valaki mondani olyan képletet, ami ismétléses permutációhoz kapcsolódik, és amellyel ezeket a gyöngyös feladatokat meg lehet oldani általános formában, mert biztosan kell létezzen ilyen képlet, megoldás, mert nem lehet az, hogy empirikusan, próbálgatásokkal oldjuk meg az ilyen feladatokat. Üdv: epsilon
|
|
| [2093] Sinobi | 2016-11-18 00:39:43 |
 Mennyire nehéz?
És, hogy célszerű megoldani az 5000 fehér, 3000 piros esetet?
|
|
| [2092] csábos | 2016-11-17 22:22:23 |
 11-es Apáczai könyv?
Képzeld el a 4 piros 4 fehért: \(\displaystyle \frac{8!}{4!4!}\)-t kéne osztni 8-cal. De ez nem egész :-(.
Ez egy nehéz feladat, próbálgatással célszerű megoldani.
|
| Előzmény: [2090] epsilon, 2016-11-17 19:00:11 |
|
|
| [2090] epsilon | 2016-11-17 19:00:11 |
 Üdv mindenkinek! Lenne egy kérdésem, mert nem jutok dűlőre. Van 3 piros és 5 fehér gyöngy. Ezek segítségével hány különböző karkötő fűzhető? Én ismétléses permutációval számoltam ki 8!/3!*5!=56 és mivel a körön akárhol elvágható a karkötő, ezért ezen elvágásokból kifolyólag, 8-al el kell osztani az előbbi eredményt, így 56:8=7 adódik. Ellenben a megoldásnál a könyvben így okoskodnak: A 3 piros gyöngy a karkötőt három ívre bontják: a három ívre ráhelyezzük az 5 fehér gyöngyöt. (forgásszimmertia miatt az ívek egyenrangúak). A fehér gyöngyök száma egyes íveken: 005, 014, 113, 122, 023. Tehát 5 különböző karkötő van. melyik a helyes válasz, az 5 vagy a 7? Hol a másik megoldásban a hiba? Előre is köszönöm, üdv: epsilon
|
|











