|
| [2143] jonas | 2017-11-29 17:06:20 |
 Ez egy tanulságos Markov-láncos feladat, érdemes végigszámolni.
Legyen a húzások száma \(\displaystyle T \). Minden \(\displaystyle 0 \le t < T \) egészre nézzük meg, hogy \(\displaystyle t \) húzás után a legközelebbi húzásban hány cetli közül kell húzni, ez legyen \(\displaystyle X_t \), valamint legyen \(\displaystyle Y_t \) azon törpék száma, akik önmagukat húzzák ebben a húzásban. Tehát \(\displaystyle 0 \le t < T \) esetén \(\displaystyle 2 \le X_t \le 7 \). Terjesszük ki az \(\displaystyle X \) sorozatot úgy, hogy \(\displaystyle X_t = 0 \) ha \(\displaystyle T \le t \).
Nyilván \(\displaystyle X_0 = 7 \). A játék szabályai szerint ha \(\displaystyle 0 \le t < T \), akkor \(\displaystyle X_{t+1} = Y_t \), kivéve ha \(\displaystyle Y_t = 1 \), amely esetben \(\displaystyle X_{t+1} = 7 \). Mármost rögzített \(\displaystyle X_t \) mellett \(\displaystyle Y_t \) eloszlása nem függ az előzményektől. Az eloszlást pontosan meg is tudjuk adni: \(\displaystyle P(Y_t = y \mid X_t = x) = \textrm{A008290}(y, x)/x! \). Itt az A008290(y, x) szám x elem azon permutációinak a száma, amiben pontosan y fixpoint van, az OEIS A008290 sorozata szerint. Ez a valószínűség nulla, ha \(\displaystyle x < y \). Íme a feltételes eloszlások táblázata.
| \(\displaystyle x =\) | 2 | 3 | 4 | 5 | 6 | 7 |
| \(\displaystyle P(Y_t=0 \mid X_t=x) =\) | 1/2 | 2/6 | 9/24 | 44/120 | 265/720 | 1854/5040 |
| \(\displaystyle P(Y_t=1 \mid X_t=x) =\) | 0 | 3/6 | 8/24 | 45/120 | 264/720 | 1855/5040 |
| \(\displaystyle P(Y_t=2 \mid X_t=x) =\) | 1/2 | 0 | 6/24 | 20/120 | 135/720 | 924/5040 |
| \(\displaystyle P(Y_t=3 \mid X_t=x) =\) | 0 | 1/6 | 0 | 10/120 | 40/720 | 315/5040 |
| \(\displaystyle P(Y_t=4 \mid X_t=x) =\) | 0 | 0 | 1/24 | 0 | 15/720 | 70/5040 |
| \(\displaystyle P(Y_t=5 \mid X_t=x) =\) | 0 | 0 | 0 | 1/120 | 0 | 21/5040 |
| \(\displaystyle P(Y_t=6 \mid X_t=x) =\) | 0 | 0 | 0 | 0 | 1/720 | 0 |
| \(\displaystyle P(Y_t=7 \mid X_t=x) =\) | 0 | 0 | 0 | 0 | 0 | 1/5040 |
A fentiekből az is következik, hogy ha rögzítjük \(\displaystyle x \)-et ahol \(\displaystyle 1 < x \), akkor az \(\displaystyle X_t = x \) feltétel mellett \(\displaystyle X_{t+1} \) eloszlása független az előzményektől, vagyis az \(\displaystyle X_0, \dots, X_{t-1} \) számoktól (és mellesleg még a húzott nevektől is), és ez a feltételes eloszlás bármely \(\displaystyle t \)-re ugyanaz. Ez azt jelenti, hogy \(\displaystyle X \) egy stacionáris markov lánc. Mivel \(\displaystyle X_{t+1} \) az \(\displaystyle Y_t \) fent leírt függvénye eloszlásból, és \(\displaystyle Y_t \) feltételes eloszlását az előbb kiszámoltuk, ezért \(\displaystyle X_{t+1} \) feltételes eloszlását (az átmenet valószínűségeket) is meg tudjuk adni.
| \(\displaystyle x =\) | 2 | 3 | 4 | 5 | 6 | 7 |
| \(\displaystyle P(X_{t+1}=0 \mid X_t=x) =\) | 1/2 | 2/6 | 9/24 | 44/120 | 265/720 | 1854/5040 |
| \(\displaystyle P(X_{t+1}=2 \mid X_t=x) =\) | 1/2 | 0 | 6/24 | 20/120 | 135/720 | 924/5040 |
| \(\displaystyle P(X_{t+1}=3 \mid X_t=x) =\) | 0 | 1/6 | 0 | 10/120 | 40/720 | 315/5040 |
| \(\displaystyle P(X_{t+1}=4 \mid X_t=x) =\) | 0 | 0 | 1/24 | 0 | 15/720 | 70/5040 |
| \(\displaystyle P(X_{t+1}=5 \mid X_t=x) =\) | 0 | 0 | 0 | 1/120 | 0 | 21/5040 |
| \(\displaystyle P(X_{t+1}=6 \mid X_t=x) =\) | 0 | 0 | 0 | 0 | 1/720 | 0 |
| \(\displaystyle P(X_{t+1}=7 \mid X_t=x) =\) | 0 | 3/6 | 8/24 | 45/120 | 264/720 | 1856/5040 |
Most akkor számoljuk ki \(\displaystyle T \) várható értékét. Erre stacionáris Markov-láncoknál a szokásos módszer a következő. Jelölje a maradék lépések számának, vagyis \(\displaystyle (T-t) \)-nek, a várható értékét \(\displaystyle a_x \) az \(\displaystyle X_t = x \) feltétel mellett. A fentiek miatt a maradék lépések számának feltételes eloszlása is független az előzményektől, és \(\displaystyle t \)-től is. Nyilván \(\displaystyle a_0 = 0 \). A többi (\(\displaystyle 2 \le x \le 7\)) esetre felírhatunk egy-egy lineáris egyenletet a fenti átmenet valószínűségek alapján.
\(\displaystyle a_x = 1 + \sum_k P(X_{t+1}=k \mid X_t=x) \cdot a_k \)
Az egyenletrendszer megoldása után, mivel \(\displaystyle X_0 = 7 \), ezért a húzások számának várható értéke \(\displaystyle a_7 \).
A konkrét esetben az egyenletrendszer a következő.
\(\displaystyle
(a_2, a_3, a_4, a_5, a_6, a_7) \cdot
\begin{pmatrix}
1/2-1 &0 &6/24 &20/120 &135/720 & 924/5040 \\
0 &1/6-1 &0 &10/120 & 40/720 & 315/5040 \\
0 &0 &1/24-1 & 0 & 15/720 & 70/5040 \\
0 &0 &0 & 1/120-1 & 0 & 21/5040 \\
0 &0 &0 & 0 & 1/720-1 & 0 \\
0 &3/6 &8/24 &45/120 &264/720 &1856/5040-1 \\
\end{pmatrix} =
\)
\(\displaystyle
= (-1, -1, -1, -1, -1, -1)
\)
Ennek a megoldása
\(\displaystyle
(a_2, a_3, a_4, a_5, a_6, a_7) = (9713740330, 13115308479, 11826442740, 12225059935, 12123252750, 12145107135) / 4856870165
\)
Így a sorsolások átlagos száma \(\displaystyle a_7 = 12145107135/4856870165 \), ami körülbelül 2.50.
|
| Előzmény: [2142] marcius8, 2017-11-28 12:15:32 |
|
| [2142] marcius8 | 2017-11-28 12:15:32 |
 Igyekszem pontosabban megfogalmazni az előbbi felvetésemet. Tehát a hét törpe (Szund, Vidor, Hapci, Kuka, ....) mindegyike felírja a saját nevét egy papírra, ezeket a papírokat egy dobozkába teszik, ezután mindegyik törpe pontosan egy papírt húz a dobozkából. Ha elsőre mindenki más nevét húzza, akkor mindenki annak azt ajándékozza meg, akinek a nevét húzta. (Ennek lesz "1/e" a valószínűsége.) Ebben az esetben a "ki kit ajándékoz meg" sorsolás eredményes, és ekkor a sorsolásnak vége. Akkor van baj, ha van olyan törpe, aki a saját nevét húzta, ekkor a sorsolást a következő szabályok szerint ismétlik meg:
- Ha több, mint 1 törpe húzta a saját nevét valamelyik megismételt sorsolás esetén, akkor ezek a törpék egymás közt újra megismétlik a sorsolást.
- Ha pontosan 1 törpe húzta a nevét, akkor a sorsolást az összes törpe részvételével megismétlik, mert ez így igazságos.
- Ha valamelyik megismételt sorsolás esetén már nincs olyan törpe, aki a saját nevét húzta, akkor a sorsolás eredményes, a sorsolásnak vége, és ekkor minden törpe azt ajándékozza meg, akinek a nevét húzta.
Ekkor várhatóan hány sorsolás után lesz az, hogy minden törpe más törpének a nevét húzta?
|
| Előzmény: [2141] marcius8, 2017-11-28 09:31:52 |
|
| [2141] marcius8 | 2017-11-28 09:31:52 |
 Nemsokára itt a karácsony. A hét törpe is készül egymás megajándékozására. Ezért a hét törpe mindegyike felírja a saját nevét egy kis papírra, a papírokat összehajtva beteszik egy dobozkába. Ezután a hét törpe mindegyike húz a dobozkából pontosan egy papírt, és minden törpe annak ad ajándékot, akinek a nevét húzta. (Ebben még semmi különös nincs.) De előfordulhat, hogy lesznek olyan törpék, akik a saját nevüket húzzák (ennek durván "1/e" a valószínűsége, ami nem elhanyagolható), ezek a törpék egymás közt újra megismétlik ezt a sorsolást. Ha megint lesznek ilyen törpék, akkor ezek a törpék egymás közt újra megismétlik ezt a sorsolást.... Végül előfordulhat az is, hogy az első sorsoláskor, vagy akármelyik sorsoláskor pontosan egy törpe húzza a saját nevét, ekkor a sorsolást mind a hét törpe újra kezdi. Várhatóan hány sorsolásra kerül sor?
|
|
| [2140] marcius8 | 2017-10-08 13:47:42 |
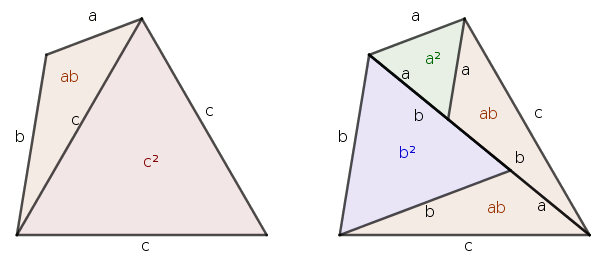
 Nagyon jók a #2138 és #2137 bizonyítások! A 90°-os háromszögre érvényes Pitagorasz-tétel területátdarabolós bizonyításánál a terület fogalma triviálisnak tűnik. De ezek a bizonyítások arra is rávilágítanak, hogy a terület fogalma egyáltalán nem olyan triviális!!!
|
|
| [2139] marcius8 | 2017-10-05 08:11:06 |
 JÉÉÉ!!!!!! Köszi a bizonyításokat FM! Hálám örökké üldözni fog!!!!
|
|
|
|
| [2136] Fálesz Mihály | 2017-10-04 19:58:00 |
 A 60 fokos esetben, sőt, a koszinusz-tétel általános esetére is működik a 2132-beli módszer: az \(\displaystyle AB\) egyenesen felvesszük azokat az \(\displaystyle X\) és \(\displaystyle Y\) pontokat, amelyekre \(\displaystyle ABC\triangle \sim ACY\triangle \sim CBX\triangle\).
|
 |
| Előzmény: [2135] marcius8, 2017-10-04 19:21:54 |
|
| [2135] marcius8 | 2017-10-04 19:21:54 |
 A #2134 és a #2132 bizonyítások nagyon jók, nagyon szépen köszönöm! A #2132 bizonyítás nagyon tetszik, mert analógiát teremt a derékszögű háromszög és a 120°-os háromszög között!!! Magam részéről egy terület-átdarabolós bizonyítást próbáltam keresni, de ez még eddig nem sikerült. (A derékszögű háromszögre érvényes Pitagorasz-tétel legismertebb bizonyítása úgy történik, hogy egy négyzetet kétféleképpen darabolnak fel. Euklidesz is terület-átdarabolással bizonyítja a Pitagorasz-tételt.) Szóval, ha még valaki tudna a 120°-os háromszögre vagy a 60°-os háromszögre érvényes összefüggésre egy terület-átdarabolós bizonyítást annak is nagyon hálás lennék!!!!
|
|
| [2134] Lpont | 2017-10-04 15:47:01 |
 Kedves Zoltán!
Egy lehetséges megoldás a 60 fokos háromszögre:
(1) Ha ABC egyenlő szárú, akkor szabályos is egyúttal, az állítás triviálisan igaz.
(2) Ha az oldalak páronként különböznek, akkor nyilván van kisebb és nagyobb szög is 60-nál, legyen pl. a>c>b.
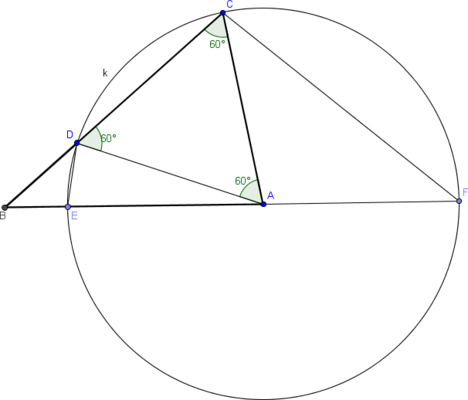
Mérjük fel b oldal hosszát rendre C-ből B felé a CB szakaszra, A-ból B-felé és vele ellentétes irányba is az az AB egyesre, kapjuk a D,E,F pontokat.
A származtatás miatt ACD szabályos, AFC és ADE egyenlő szárú háromszög. Ha A-nál lévő szög alfa, akkor F-nél alfa/2 és DAE szög alfa-60, ezért ADE szög 120-alfa/2. CDEF négyszög húrnégyszög, hiszen F-nél és D-nél lévő szögeinek összege 180.
B pontnak a húrnégyszög körülírt k körére vonatkozó hatványa: BE*BF=BD*BC, azaz (c-b)*(c+b)=(a-b)*a, ahonnan zárójelfelbontás és rendezés után a bizonyítandó állítást kapjuk.
|
 |
| Előzmény: [2131] marcius8, 2017-10-03 11:21:13 |
|
|
| [2132] Fálesz Mihály | 2017-10-04 06:11:28 |
 Szerintem ez jó iskolai gyakorlat lehetne. Amikor a befogó- és a magasságtételt tanítjuk, majd a befogótételből bebizonyítjuk a Pitagorasz-tételt, fel lehet adni, hogy ezek mintájára csinálják meg a 120 fokos esetet.
A bizonyítás alapja az önhasonlóság; ha a derékszögű háromszöget kettéosztjuk az átfogóhoz tartozó magassággal, a két rész hasonló lesz az eredeti háromszöghöz.
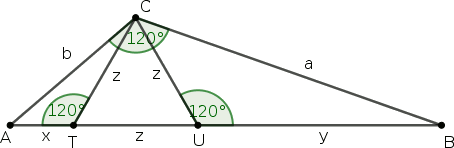
Ha a háromszög nem derékszögű, hanem van egy mondjuk 120 fokos szöge, akkor a magasság helyett belerajzolhatunk egy szabályos háromszöget. Az ábra betűzésével \(\displaystyle ABC\triangle \sim ACT\triangle \sim CBU\triangle\), és persze \(\displaystyle c=x+y+z\). A hasonlóságokból
\(\displaystyle
\frac{a}{c}=\frac{y}{a}=\frac{z}{b}, \quad
\frac{b}{c}=\frac{x}{b}=\frac{z}{a} \quad\text{és}\quad
\frac{a}{b}=\frac{y}{z}=\frac{z}{x}.\)
Ezeket átszorozva,
\(\displaystyle
a^2 = cy, \quad b^2=cx, \quad ab=cz, \quad z^2=xy.
\)
Az első kettő megfelel a befogótételnek, a harmadik a terület kétféle felírása, a negyedik a magasságtétel megfelelője. Az első hármat összeadva,
\(\displaystyle
a^2+ab+b^2 = c(x+y+z) = c^2.
\)
|
 |
| Előzmény: [2131] marcius8, 2017-10-03 11:21:13 |
|
| [2131] marcius8 | 2017-10-03 11:21:13 |
 Esetleg, ha valaki az előző hozzászólásomban említett, a 60°-os háromszögre és a 120°-os háromszögre vonatkozó összefüggéseket be tudná bizonyítani nekem a 90°-os háromszögre vonatkozó Pitagorasz-tétel felhasználása nélkül, annak nagyon hálás lennék. Vajon a Pitagorasz-tétel bizonyításához hasonlóan be lehet bizonyítani a 60°-os háromszögre és a 120°-os háromszögre vonatkozó összefüggéseket?
|
|
| [2130] marcius8 | 2017-09-29 10:03:24 |
 Geometriában az egyik legfontosabb tétel a Pitagorasz-tétel, amely szerint ha egy derékszögű háromszög befogói \(\displaystyle a\) és \(\displaystyle b\), átfogója \(\displaystyle c\), akkor a következő összefüggés teljesül:
\(\displaystyle a^2+b^2=c^2\)
Ennek a tételnek a felhasználásával a következő összefüggések vezethetőek le:
Legyenek egy 60°-os háromszögnek a 60° melletti oldalai (nevezzük befogóknak) \(\displaystyle a\) és \(\displaystyle b\), a 60°-os szöggel szemközti oldala (nevezzük átfogónak) \(\displaystyle c\). Ekkor a következő összefüggés teljesül (60°-os háromszögre érvényes Pitagorasz-tétel):
\(\displaystyle a^2-ab+b^2=c^2\)
Legyenek egy 120°-os háromszögnek a 120° melletti oldalai (nevezzük befogóknak) \(\displaystyle a\) és \(\displaystyle b\), a 120°-os szöggel szemközti oldala (nevezzük átfogónak) \(\displaystyle c\). Ekkor a következő összefüggés teljesül (120°-os háromszögre érvényes Pitagorasz-tétel):
\(\displaystyle a^2+ab+b^2=c^2\)
A probléma a következő: Először megtanuljuk a derékszögű háromszögre a Pitagorasz-tételt, majd csak ennek felhasználásával bizonyítjuk a 60°-os háromszögre érvényes Pitagorasz-tételt, és a 120°-os háromszögre érvényes Pitagorasz-tételt. De mi lenne, ha először a 60°-os háromszögre érvényes Pitagorasz-tételt tanulnánk, és csak ennek felhasználásával hogyan kellene bizonyítani a másik két Pitagorasz-tételt? Vagy mi lenne, ha először a 120°-os háromszögre érvényes Pitagorasz-tételt tanulnánk, és csak ennek felhasználásával hogyan kellene bizonyítani a másik két Pitagorasz-tételt? Várom mindenkinek megtisztelő válaszát: Bertalan Zoltán.
|
|
| [2129] marcius8 | 2017-08-30 00:02:02 |
 Ok, teljesen igaz a megjegyzés. Akkor úgy pontosítok, hogy a mérkőzésenkénti gólok száma 3 várható értékű Poisson-eloszlást követ úgy, hogy a mérkőzés bármely viszgált időszaka alatt esett gólok száma is Poisson eloszlású. Ekkor feltehető, hogy a vizsgált időszak alatti gólok számának várható értéke úgy aránylik a teljes mérkőzés alatti gólok számának várható értékéhez, mint a vizsgált időszak hossza a teljes mérkőzés idejéhez.
|
| Előzmény: [2128] jonas, 2017-08-29 22:33:46 |
|
| [2128] jonas | 2017-08-29 22:33:46 |
 Szerintem ahhoz, hogy ezt meg lehessen mondani, nem elég annyi megkötés a modellre, hogy “A mérkőzésenkénti gólok száma Poisson-eloszlást követ”. Ha például minden jelenlegi mérkőzésnek a vége felé könnyebb gólt rúgni, mint az elején, akkor az új szabály sokszor fog hosszabbítást és több gólt eredményezni, de ettől még igaz lehet a feltételed.
|
| Előzmény: [2127] marcius8, 2017-08-29 18:16:54 |
|
| [2127] marcius8 | 2017-08-29 18:16:54 |
 Tegyük fel, hogy minden futballmérkőzés pontosan 90 percig tart, és minden mérkőzésen átlagosan 3 gól esik. A mérkőzésenkénti gólok száma Poisson-eloszlást követ. Most nagy hirtelen a nagyokos szabályalkotók összegyűlnek, és kitalálják azt az új szabályt, hogy ha akármelyik mérkőzésen egy gól esik, akkor a mérkőzés nem ér véget automatikusan 90 perc után, hanem a gól után pontosan 10 percig még tart a mérkőzés, azaz 10 perc hosszabbítás következik. Nyilván, ha az utolsó gól a mérkőzés 80.-ik perce előtt esik, akkor a mérkőzés automatikusan véget ér 90 perc után. Milyen eloszlást követ ekkor a mérkőzések időtartalma? Vigyázat, ha a mérkőzés hosszabbításában is gól születik, akkor a gól után a 10 perc hosszabbítás mérése automatikusan újra kezdődik.
|
|
|
| [2125] marcius8 | 2017-06-10 22:00:49 |
 Keresek olyan mindenhol differenciálható komplex függvényt, amelynek az összes gauss-egész a zérushelye, de csak a gauss-egészek a zérushelyei. Ha lehet, a függvényt az ismert elemi függvények segítségével és a négy alapművelet véges sokszori alkalmazásával írjuk fel. Előre is köszönöm mindenkinek a segítségét!
|
|
| [2124] yield | 2017-03-04 07:56:41 |
 Mind a két megjegyzésed jogos, köszönöm!
1. Az óramutató képletem nem volt jó: 30*(t/30) helyett 30*(t/60) a jó. Így megoldva az egyenleteket kijön a 12/11 óra.
2. A külőnbség abszolut értéke egy órán belül (ha t: 0 és 60 között) kétszer lesz 110. Pontosítani kell a feladatkiírást
|
| Előzmény: [2123] csábos, 2017-03-03 20:23:06 |
|
| [2123] csábos | 2017-03-03 20:23:06 |
 A két eredmény nem ugyanannyi. Az 1 óra 6 perc nem 12/11 óra. Ráadásul ma 6-tól 7-ig az órámat néztem, és a két mutató kétszer is 110 fokot zárt be egymással. Ez 110 fok helyett szinte minden szögre igaz. 7-kor 150 fokos szöget zárnak be, így nem sokkal előtte is meg kell hogy valósuljon a 110 fok. Az eredmény irányított szögek esetén tényleg ugyanannyi minden szögre.
|
| Előzmény: [2122] epsilon, 2017-03-03 16:19:34 |
|
|
| [2121] yield | 2017-03-03 12:06:15 |
 Fapados megoldás:
I. 18 óra után
- kismutató helyzete: 180*(\(\displaystyle t_1\)/30)
- nagymutató helyzete: 30*(\(\displaystyle t_1\)/30) + 180
- egyenlet: kettő külőnbsége = 110
II. 19 óra után
- kismutató helyzete: 180*(\(\displaystyle t_2\)/30)
- nagymutató helyzete: 30*(\(\displaystyle t_2\)/30) + 210
- egyenlet: kettő külőnbsége = 110
Ebből:
- \(\displaystyle t_1\) = 14 (18:14-kor volt 110 fokos a külőnbség)
- \(\displaystyle t_2\) = 20 (19:20-kor volt 110 fokos a külőnbség)
Akkor feladat megoldása: (19:20 - 18:14) = 1óra 6perc.
|
| Előzmény: [2120] epsilon, 2017-03-03 07:58:10 |
|
|