| [2180] marcius8 | 2018-06-23 20:14:32 |
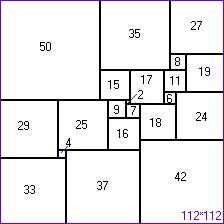
 Arie Duijvestijn (remélem, jól írom a nevet) holland matematikus egy négyzetet felbontott különböző méretű négyzetekre. (Lásd: ábra). Vajon egy szabályos háromszöget is fel lehet bontani különböző méretű szabályos háromszögekre?
|
 |
|
| [2179] marcius8 | 2018-02-23 11:18:54 |
 Középiskolában tanítják (tanítom) a visszatevés nélküli mintavételt és a visszatevéses mintavételt. A visszatevés nélküli mintavétel azt jelenti, hogy egy alapsokaságból egyszerre kiveszek valamennyi elemet, és a kivett elemeket tekintem egy mintának. A visszatevéses mintavétel azt jelenti, hogy az alapsokaságból valamennyiszer véletlenszerűen kiveszek egy elemet, és a kivett elemet mindig visszateszem. És azt is tudjuk, hogy a reprezentatív minta valószínűsége a legnagyobb, mint a visszatevéses mintavétel esetében, mind a visszatevés nélküli mintavétel esetében. DE!!! Tekintsük a következő példát:
Van 10 darab fehér golyó, 20 darab világosszürke golyó, 30 darab sötétszürke golyó, 40 darab fekete golyót. Most úgy készítek egy 50 elemű mintát, hogy kiveszek 5 darab golyót, megnézem ezt az 5 golyót, visszateszem az alapsokaságba, elkeverem az alapsokaságot, megint kiveszek 5 darab golyót,.... ezt 10-szer csinálom meg. Tulajdonképpen ez is visszatevéses mintavétel, csak a mintavétel 5-ösével történik. Ilyenkor milyen összetételű minta a legvalószínűbb, és mennyi ennek a valószínűsége?
|
|
|
| [2177] marcius8 | 2018-02-13 13:18:31 |
 Keresem az \(\displaystyle a_{n+1}=\sqrt{2a_n+3}\), \(\displaystyle a_1=4\) sorozat explicit alakját. Minden segítséget előre is köszönök! Amit tudok, az hogy a sorozat határértéke 3, és szigorúan monoton csökkenő. Tisztelettel: Bertalan Zoltán.
|
|
| [2174] Fálesz Mihály | 2018-02-02 10:07:26 |
 A két példád között különbség van, és a lényeg a kiválasztási axióma szerepe.
A transzcendens számok halmaza egy konkrét, a kiválasztási axióma használata nélkül is jól megadható halmaz. Az \(\displaystyle \mathbb{R}\)-rel való megfelelést sem nehéz kitalálni, ehhez elég az algebrai számok egy felsorolása, de még felsorolás nélkül sem nehéz.
A bázis esetében a nehézség nem a bijekcióval kezdődik, hanem azzal, hogy melyik bázisról van szó a \(\displaystyle 2^{2^{\aleph_0}}\) lehetőség közül. Azt, hogy egyáltalán létezik bázis, a Zorn-lemmából, vagy a kiválasztási axióma valamelyik más ekvivalens formájából szoktuk bizonyítani. Ha mondasz egy konkrét bázist, én majd mondok hozzá egy konkrét bijekciót az \(\displaystyle \mathbb{R}\)-rel... :-)
|
| Előzmény: [2173] marcius8, 2018-02-01 08:25:51 |
|
| [2173] marcius8 | 2018-02-01 08:25:51 |
 Nem is ezzel van a problémám, hogy oda-vissza létezik kölcsönösen egyértelmű megfeleltetés a valós számok halmaza és egy adott kontinuum-számosságú halmaz között. Hanem azzal, hogy egy adott kontinuum-számosságú halmaz és a valós számok halmaza között nem tudok egy konkrét megfeleltetést létesíteni.
Pl. A transzcendens számok kontinuum-számosságú halmazt alkotnak. Adjunk meg konkrétan egy kölcsönösen egyértelmű megfeleltetést a transzcendens számok és a valós számok között.
Pl. Tekintsük a valós számokat mint a racionális számok feletti vektorteret. Ekkor ennek a vektortérnek van bázisrendszere, és ennek a bázisrendszernek az elemszáma kontinuum-számosságú. Adjunk meg egy kölcsönösen egyértelmű megfeleltetést ezen bázisrendszer és a valós számok között.
|
| Előzmény: [2172] Fálesz Mihály, 2018-01-30 22:30:14 |
|
| [2172] Fálesz Mihály | 2018-01-30 22:30:14 |
 Tehát, ha van egy kontinuum számosságú \(\displaystyle K\) halmazunk, akkor van \(\displaystyle f:\mathbb{R}\to K\) bijekció is.
Az \(\displaystyle \mathbb{R}\)-et \(\displaystyle n\) kontinuum számosságú részre osztjuk — mondjuk \(\displaystyle n\) diszjunkt intervallumra: \(\displaystyle \mathbb{R}=R_1\cup\dots\cup R_n\). Ezután részhalmazokat visszaképezzük az eredeti halmazba:
\(\displaystyle K = f(R_1) \cup \ldots \cup f(R_n). \)
|
| Előzmény: [2171] marcius8, 2018-01-30 08:28:08 |
|
|
|
| [2169] marcius8 | 2018-01-29 09:24:39 |
 Nekem elég, ha egy ellenség által megadott kontinuumszámosságú halmazt egy konkrét algoritmussal két kontinuumszámosságú részre osztjuk. (Nyilván a két rész metszete üres halmaz, és a két rész uniója az ellenség által megadott kontinuumszámosságú halmaz.)
|
| Előzmény: [2165] Fálesz Mihály, 2018-01-10 07:59:00 |
|
| [2168] marcius8 | 2018-01-21 08:41:51 |
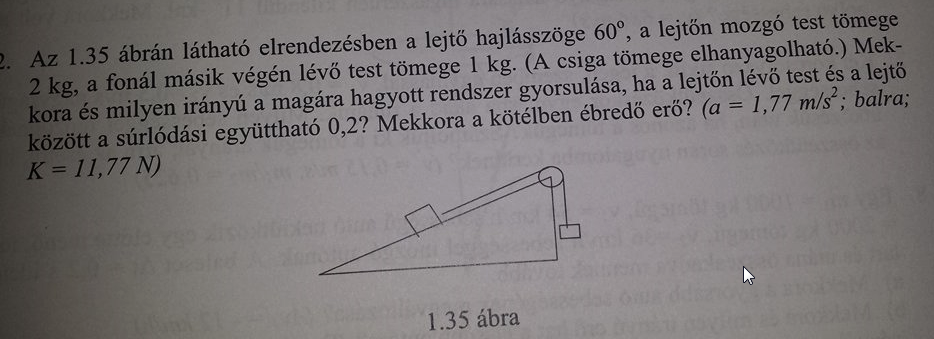
 \(\displaystyle m_1=2\rm{kg}\), \(\displaystyle m_2=1\rm{kg}\), \(\displaystyle g=10\rm{méter/sec^2}\), \(\displaystyle \alpha=60°\), \(\displaystyle \mu=0,2\).
Legyen \(\displaystyle F_{tartó}\) a lejtő által kifejtett, az \(\displaystyle m_1\) testre ható tartóerő, ez az erő a lejtő felületére merőleges, és az ábra szerint ferdén balra és felfelé mutat. Az \(\displaystyle m_1\) testre hat az \(\displaystyle G_1=m_1g\) súlyerő, ennek az iránya függőlegesen lefelé mutat. Ezt az erőt érdemes a lejtővel párhuzamos \(\displaystyle G_{1párh}=m_1g*\sin(\alpha)\) és \(\displaystyle G_{1mer}=m_1g*\cos(\alpha)\) erőkre bontani. Az \(\displaystyle m_1\) testre hat még a \(\displaystyle K\) kötélerő, ennek iránya a lejtővel párhuzamos, és az ábra szerint jobbra és felfelé mutat a csiga irányába. Az \(\displaystyle m_1\) testre hat még az \(\displaystyle S\) súrlódási erő, amelynek iránya a lejtővel párhuzamos, az \(\displaystyle m_1\) test mozgásával ellentétes. Az \(\displaystyle m_2\) testre hat a \(\displaystyle G_2=m_2g\) súlyerő, ennek iránya függőlegesen lefelé mutat. Az \(\displaystyle m_2\) tömegű testre hat a \(\displaystyle K\) kötélerő, ennek iránya függőlegesen felfelé mutat.
Az \(\displaystyle m_1\) tömegű test a lejtőre merőlegesen nem mozog, ezért a rá ható és a lejtőre merőleges erők kiegyenlítik egymást, azaz \(\displaystyle F_{tartó}=G_{1mer}\) azaz \(\displaystyle F_{tartó}=m_1g*\cos(\alpha)\). A súrlódási erő definíciója miatt \(\displaystyle S=\mu*F_{tartó}=\mu*m_1g*\cos(\alpha)\) Tegyük fel, hogy az \(\displaystyle m_1\) test a lejtőn felfelé az \(\displaystyle m_2\) test függőlegesen lefelé gyorsul. Ekkor az \(\displaystyle m_1\) testre ható \(\displaystyle S\) súrlódási erő iránya a lejtőn lefelé mutat. A két test gyorsulásának nagysága egyenlő, legyen \(\displaystyle a\) a két test gyorsulásának nagysága.
Alkalmazva Newton II. törvényét a két testre:
\(\displaystyle m_1a=K-G_{1párh}-S=K-m_1g*\sin(\alpha)-\mu*m_1g*\cos(\alpha)\)
\(\displaystyle m_2a=G_2-K=m_2g-K\)
Ekkor \(\displaystyle a=-3,1068\rm{méter/sec^2}\) és \(\displaystyle K=13,1068\rm{Newton}\) adódik. Mivel \(\displaystyle a\) értéke negatív, ezért hibás volt az a feltételezés, hogy az \(\displaystyle m_1\) test a lejtőn felfelé, az \(\displaystyle m_2\) test a lejtőn lefelé gyorsul.
Most tegyük fel, hogy az \(\displaystyle m_1\) test a lejtőn lefelé az \(\displaystyle m_2\) test függőlegesen felfelé gyorsul. Ekkor az \(\displaystyle m_1\) testre ható \(\displaystyle S\) súrlódási erő iránya a lejtőn felfelé mutat. A két test gyorsulásának nagysága egyenlő, legyen \(\displaystyle a\) a két test gyorsulásának nagysága.
Alkalmazva Newton II. törvényét a két testre:
\(\displaystyle m_1a=K-G_{1párh}-S=m_1g*\sin(\alpha)-K-\mu*m_1g*\cos(\alpha)\)
\(\displaystyle m_2a=G_2-K=K-m_2g\)
Ekkor \(\displaystyle a=1,7735\rm{méter/sec^2}\) és \(\displaystyle K=11,7735\rm{Newton}\) adódik.
|
| Előzmény: [2167] shadow, 2018-01-18 22:06:00 |
|
| [2167] shadow | 2018-01-18 22:06:00 |
 Sziasztok!
Már nagyon régen volt, és a gyakorlatvezetőim sem a legjobbak voltak. Az rémlik, hogy két komponensre kellene bontanom az erőket de már nem tudom hogyan induljak neki. Esetleg valaki tud segíteni?
|
 |
|
| [2165] Fálesz Mihály | 2018-01-10 07:59:00 |
 Csatlakozva jonashoz, a kérdésed úgy kezdődött, hogy "hogyan lehet egy kontinuum számosságú halmazt..."
Tehát a játékban kapunk az ellenségünktől egy halmazt, amiről tudni véli, de inkább be tudja bizonyítani, hogy "kontinuum számosságú", és egy \(\displaystyle n\) pozitív egészt. Nekünk az a feladatunk, hogy a halmazt valami algoritmussal \(\displaystyle n\) részre osszuk.
A kérdés: annak bizonyítása, hogy a halmaz kontinuum számosságú, nem biztosít automatikusan (például a Cantor-Schröder-Bernstein tétel segítségével) egy bijekciót valamilyen ismert, kontinuum számosságú halmazzal?
|
| Előzmény: [2162] marcius8, 2018-01-09 20:02:28 |
|
| [2164] Fálesz Mihály | 2018-01-10 07:43:04 |
 Megfelelteted a (legyen mondjuk \(\displaystyle H\)) halmazt az \(\displaystyle [0,n)\) intervallumnak vagyis veszel egy \(\displaystyle f:[0,n)\to H\) bijekciót. A \(\displaystyle [0,n)\) intervallum a szintén kontinuum számosságú \(\displaystyle [0,1),\ldots,[n-1,1)\) intervallumok uniója; ezeket külön-külön is képezheted a \(\displaystyle H\) halmazba:
\(\displaystyle
H =
f\big([0,n)\big) =
f\big([0,1)\big) \cup\ldots\cup f\big([n-1,n)\big).
\)
Véges sok helyett kontinuum sok résszel is megy: a kontinuum számosságú sík felbontható kontinuum sok párhuzamos egyenes uniójára.
|
| Előzmény: [2158] marcius8, 2018-01-06 18:23:36 |
|
| [2163] jonas | 2018-01-10 01:01:48 |
 Azt, hogy egy halmaz kontinuum számosságú, többé-kevésbé úgy definiáljuk, hogy van egy bijekció valamilyen rögzített kontinuum számosságú halmazra, mondjuk a természetes számok halmazának a hatványhalmazára. Ha be szeretnéd bizonyued tani egy konkrét halmazról, hogy tényleg kontinuum számosságú, akkor többnyire a Schröder-Bernstein tételt a legkönnyebb fölhasználni. Ez gyakran kikerülhető lenne, de könnyebb egyszer bebizonyítani azt a tételt, mint minden példához újabb konstrukciókat keresni.
|
| Előzmény: [2162] marcius8, 2018-01-09 20:02:28 |
|
| [2162] marcius8 | 2018-01-09 20:02:28 |
 Bármilyen meglepő, én is pont egy ilyen módszerre gondoltam. DE! konkrétan egy ilyen "univerzális" megfeleltetést még nem tudtam találni, ami bármilyen adott kontinuum-számosságú halmaz esetén működne.
|
| Előzmény: [2160] Sirpi, 2018-01-09 09:23:30 |
|
| [2161] jonas | 2018-01-09 17:17:54 |
 „amikre teljesül, hogy az egészrészük n-es maradéka éppen k.”
Dehát az végtelen sok vágás. Az alatt elkopik a kés. Nem lehetne valahogyan \(\displaystyle k - 1 \) vágással megoldani?
|
| Előzmény: [2160] Sirpi, 2018-01-09 09:23:30 |
|
| [2160] Sirpi | 2018-01-09 09:23:30 |
 Ha kontinuum számosságú, akkor képezhető egy bijekció a valós számok halmazával, tehát elég a valós számokat felosztani. Ott pedig a k. halmazba (\(\displaystyle k=0,1, \dots, n-1\)) tegyük bele azokat a számokat, amikre teljesül, hogy az egészrészük n-es maradéka éppen k.
|
| Előzmény: [2158] marcius8, 2018-01-06 18:23:36 |
|
|
| [2158] marcius8 | 2018-01-06 18:23:36 |
 Hogyan lehet egy kontinuum számosságú halmazt \(\displaystyle n\) darab egyforma számosságú részre osztani?
|
|
| [2157] marcius8 | 2018-01-06 16:04:04 |
 4. Ha \(\displaystyle x=pA+qB+r\), akkor legyen \(\displaystyle f(x)=r\), \(\displaystyle g(x)=qB\), \(\displaystyle h(x)=pA\).
5. \(\displaystyle u(x)=qb+r\), \(\displaystyle v(x)=pA-r\), ekkor \(\displaystyle u(x)+v(x)=pA+qB\) teljesül.
Köszönöm a segítséget!
|
| Előzmény: [2153] jonas, 2018-01-03 01:54:24 |
|
| [2156] jonas | 2018-01-03 23:09:49 |
 A 4-eshez a következőképpen kezdj hozzá. A függvény \(\displaystyle x \) argumentumát próbáld meg a 3. feladatban leírt módon felírni. Ha semmilyen \(\displaystyle p, q, r \) racionális számokra nem teljesül \(\displaystyle x = pA + qB + r \), akkor legyen \(\displaystyle f(x) = 0 \). Ez még nem rontja el, hogy a függvénynek \(\displaystyle A \) periódusa, mert ha \(\displaystyle x \) nem írható föl így, akkor \(\displaystyle x + A \) sem, ezért \(\displaystyle f(x + A) = 0 \). Ha van \(\displaystyle x = pA + qB + r \) megoldás, akkor a \(\displaystyle p, q, r \) számokból add meg valahogy \(\displaystyle f(x) \) értékét. Mit kell csinálni ahhoz, hogy \(\displaystyle f(x) = f(x + A) \) teljesüljön? Hogyan lehet elrontani az \(\displaystyle 1 \) periódust?
Az 5. feladathoz a következőt gondold át. Ha az \(\displaystyle f, g \) függvények minden valós számon értelmezve vannak, és mindkettő \(\displaystyle A \)-val periodikus, akkor mit mondhatsz az \(\displaystyle f + g \) függvényről? Ha \(\displaystyle f \) periodikus \(\displaystyle B \) periódussal, de \(\displaystyle g \) nem, akkor mit mondhatsz az \(\displaystyle f + g \) függvényről?
|
| Előzmény: [2155] marcius8, 2018-01-03 19:21:25 |
|
|
|
| [2153] jonas | 2018-01-03 01:54:24 |
 Hadd próbáljalak rávezetni.
1. Bizonyítsd be, hogy létezik irracionális szám. Erre két ismert bizonyítás is van: az elemi és a számosságos. A te kérdésedhez elég csak az egyik bizonyítást ismerni, de hosszú távon hasznos mindkettőt tudni.
2. Bizonyítsd be, hogy létezik két valós szám \(\displaystyle A, B \) úgy, hogy \(\displaystyle A, B, 1 \) lineárisan független a racionális számok fölött, vagyis bármely \(\displaystyle p, q, r \) racionális számokra ha \(\displaystyle pA + qB + r = 0 \), akkor \(\displaystyle p = q = r = 0 \).
3. Ha rögzítettek az \(\displaystyle A, B \) számok a fenti tulajdonsággal, akkor lásd be, hogy bármely \(\displaystyle x \) valós számot legfeljebb egyféleképpen lehet \(\displaystyle x = pA + qB + r \) alakban felírni úgy, hogy \(\displaystyle p, q, r \) három racionális szám legyen.
4. Adott \(\displaystyle A, B \) számokhoz a fenti tulajdonsággal konstruálj egy olyan \(\displaystyle f \) valós-valós függvényt, hogy \(\displaystyle f \)-nek periódusa \(\displaystyle A \) és \(\displaystyle B \) is, de \(\displaystyle 1 \) nem periódusa. Hasonlóan konstruálj egy olyan \(\displaystyle g \) valós-valós függvényt, aminek \(\displaystyle A \) és \(\displaystyle 1 \) periódusai, de \(\displaystyle B \) nem; és egy \(\displaystyle h \) valós-valós függvényt, aminek \(\displaystyle B \) és \(\displaystyle 1 \) periódusa, de \(\displaystyle A \) nem.
5. Ha adott három függvény \(\displaystyle f, g, h \) a fenti tulajdonságokkal, akkor rakj össze belőlük két valós-valós függvényt \(\displaystyle u, v \) néven úgy, hogy \(\displaystyle u \)-nak \(\displaystyle A \) periódusa de \(\displaystyle B \) nem periódusa és \(\displaystyle 1 \) sem periódusa; \(\displaystyle v \)-nek \(\displaystyle B \) periódusa de \(\displaystyle A \) nem periódusa és \(\displaystyle 1 \) sem periódusa; \(\displaystyle u + v \)-nek \(\displaystyle 1 \) periódusa de \(\displaystyle A \) nem és \(\displaystyle B \) sem.
Ezek együtt elvileg megválaszolják a kérdésedet. Ha nem elég, akkor mondjad, hogy hol akadtál el. Ha mind megvan, akkor bónusznak javaslom az egyik kedvenc feladatomat.
6. Igazold, hogy van olyan ponthalmaz az egységnégyzetben, ami bármely a négyzet bármely oldalával párhuzamos (vízszintes vagy függőleges) egyenest csak véges sok pontban metsz, viszont a négyzeten mindenütt sűrű (vagyis bármely tengyelypárhuzamos téglalapot, ami teljesen a négyzeten belül helyezkedik el, legalább egy pontban metsz).
|
| Előzmény: [2151] marcius8, 2018-01-01 12:35:31 |
|








