|
|
| [2195] Jhony | 2018-11-24 21:37:41 |
 Köszönöm szépen a hozzászólást,annyit elárulhatok,hogy a sejtésem,ami,végül is bizonyítva tétel,szóval bizonyítottan igazolja,hogy az ikerprímek sora végtelen - ami ,ha jól tudom,máig nincsen bizonyítva ....
|
| Előzmény: [2194] Lóczi Lajos, 2018-11-24 17:13:53 |
|
| [2194] Lóczi Lajos | 2018-11-24 17:13:53 |
 Látatlanban nehéz tanácsot adni. Minden attól függ, a sejtés mennyire "érdekes". Esetleg magát az állítást beírhatod ide is, hátha néhányan véleményt tudnak róla mondani.
|
| Előzmény: [2193] Jhony, 2018-11-23 23:35:09 |
|
| [2193] Jhony | 2018-11-23 23:35:09 |
 Tisztelt ,,Mindenki" ! - tudom,nagyképűnek hangzik,de akkor is ez az igazság,vagyis - úgy gondolom - szeptember 6-dikán találtam egy matematikai sejtést,amit teljes indukcióval be is tudok bizonyítani - kérdésem : ebben a helyzetben hogyan tovább ? mi lehet , mi legyen a következő lépés ? a kollégáim - van köztük diplomás is - azt javasolták keressem fel az MTA - át és ott kérdezzek rá ? ...,előbb még is úgy gondoltam felteszem a kérdést itt remélve kapok kisegítő ,,használható" válaszokat ... nagyonszépen köszönök minden választ ,segítséget !
|
|
|
|
|
| [2189] marcius8 | 2018-10-23 14:57:32 |
 Az könnyen látható, hogy a \(\displaystyle q_1\) és \(\displaystyle q_2\) kvaterniókhoz létezik olyan \(\displaystyle q\) kvaternió, amelyre teljesül, hogy a \(\displaystyle q_1\) kavternió a \(\displaystyle q\) kvaterniónak valamilyen (egész) kitevőjű hatványa, és a \(\displaystyle q_2\) kvaternió a \(\displaystyle q\) kvaterniónak valamilyen (egész) kitevőjű hatványa, akkor \(\displaystyle q_1*q_2=q_2*q_1\) egyenlet teljesül. Igaz-e ennek az állításnak a megfordítása?
|
|
| [2188] marcius8 | 2018-07-21 16:55:42 |
 \(\displaystyle n\) darab egymással szabályos ötszöget feldarabolunk az átlói mentén. Így keletkezik \(\displaystyle 5n\) darab egyenlő szárú háromszög, melyeknek szögei 36°, 36°, 108°, keletkezik \(\displaystyle 5n\) darab egyenlő szárú háromszög, melyeknek szögei 72°, 72°, 36°, és keletkezik \(\displaystyle n\) darab kisebb, egymással egybevágó szabályos ötszög. Milyen \(\displaystyle n\) esetén rakható össze a keletkezett síkidomokból mindegyiket pontosan egyszer felhasználva egy nagyobb szabályos ötszög?
|
|
|
|
| [2185] marcius8 | 2018-07-02 10:55:54 |
 Végül is a primnégyzetek reciprokösszege csak egy másik végtelen összeggel lett felírva, amelynek értéke el lett nevezve. Ez nagyjából annak a beismerése, hogy igazából semmit sem tudunk erről az összegről. De a [2183] kérdés nagyon jó!!!! A [2184] válasz meg érdekes. A [2183] kérdés annyira tetszett nekem, hogy ezzel kapcsolatban nekem is eszembe jutottak a következő kérdések:
Mit tudunk a \(\displaystyle 4k+1\) alakú pozitív prímek reciprokösszegéről? Mit tudunk a \(\displaystyle 4k-1\) alakú pozitív prímek reciprokösszegéről?
Mit tudunk a \(\displaystyle 6k+1\) alakú pozitív prímek reciprokösszegéről? Mit tudunk a \(\displaystyle 6k-1\) alakú pozitív prímek reciprokösszegéről?
|
| Előzmény: [2184] Lóczi Lajos, 2018-07-01 09:45:07 |
|
|
| [2183] Bátki Zsolt | 2018-06-30 15:55:57 |
 Mint tudjuk a természetes számok reciprokának az összege végtelen (divergens a sor) A prímszámokra is végtelen: azaz sum (1/p) nagyon soknál is több. Sum (1/i*i) Négyzetszámok reciprok összege (pi*pi/6, Euler alapján) véges.
De mennyi sum (1/(p*p)) azaz:prímek négyzetének reciprok összege mennyi? nem találtam erre az interneten. Próbáltam számolni de nem sokra jutottam a sejtésben, hogy mennyi. Írok rá programot, de az nem hozza ki a formulát, ha van egyáltalán. Köszi a segítségetek. 1/(2*2)+1/(3*3)+1/(5*5)+1/(7*7)+1/(11*11)+1/(13*13)+1/(17*17) =0.439...
|
|
| [2182] Erben Péter | 2018-06-30 14:00:50 |
 Jobban átgondolva a hivatkozott elemibb megoldást, látok benne egy hiányosságot (abban az esetben, amikor a legkisebb háromszög valamelyik szélen van), és nem vagyok biztos benne, hogy ez (egyszerűen) javítható.
|
| Előzmény: [2181] Erben Péter, 2018-06-30 11:08:13 |
|
| [2181] Erben Péter | 2018-06-30 11:08:13 |
 Ha jól értem, háromszögekre először W. T. Tutte bizonyította, hogy nem lehetséges ilyen felbontást csinálni. (Dissections into Equilateral Triangles, in. The Mathematical Gardner (1981))
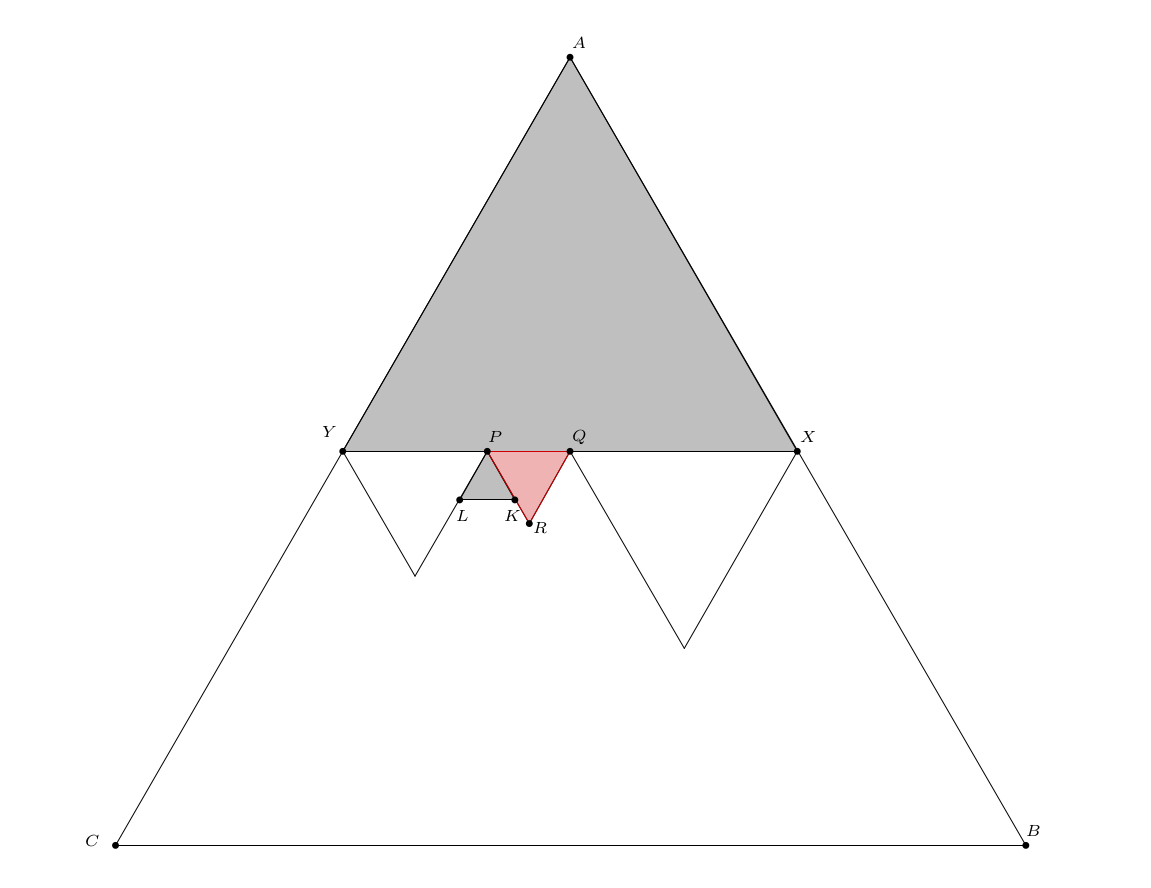
Itt van egy elemibb megoldás, ami analóg azzal, ahogy kockákra szokás bizonyítani a lehetetlenséget.
Legyen az \(\displaystyle ABC\) szabályos háromszög \(\displaystyle A\) csúcsát lefedő háromszög \(\displaystyle AXY\). Az \(\displaystyle XY\) oldalt különböző hosszú háromszög oldalak fedik, ezek közül a legrövidebb \(\displaystyle PQ\) (\(\displaystyle P\) vagy \(\displaystyle Q\) eshet az eredeti háromszög oldalára is), és a szabályos háromszög \(\displaystyle PQR\).
A \(\displaystyle P\) és \(\displaystyle Q\) csúcsú ,,felfelé álló'' háromszögek közül legalább az egyik kisebb, mint \(\displaystyle PQR\), különben ezek \(\displaystyle R\)-nél egymásba csúsznának.
Legyen mondjuk \(\displaystyle PKL\) a kisebb. Most a \(\displaystyle PKL\) háromszög átveszi \(\displaystyle AXY\) szerepét, és megint fogunk találni egy \(\displaystyle PKL\)-nél kisebb ,,felfelé álló'' szürke háromszöget a felbontásban.
Mivel a leírt logika tetszőlegesen sokáig folytatható, nem állhat véges sok háromszögből a felbontás.
|
 |
| Előzmény: [2180] marcius8, 2018-06-23 20:14:32 |
|
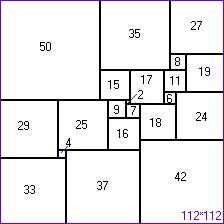
| [2180] marcius8 | 2018-06-23 20:14:32 |
 Arie Duijvestijn (remélem, jól írom a nevet) holland matematikus egy négyzetet felbontott különböző méretű négyzetekre. (Lásd: ábra). Vajon egy szabályos háromszöget is fel lehet bontani különböző méretű szabályos háromszögekre?
|
 |
|
| [2179] marcius8 | 2018-02-23 11:18:54 |
 Középiskolában tanítják (tanítom) a visszatevés nélküli mintavételt és a visszatevéses mintavételt. A visszatevés nélküli mintavétel azt jelenti, hogy egy alapsokaságból egyszerre kiveszek valamennyi elemet, és a kivett elemeket tekintem egy mintának. A visszatevéses mintavétel azt jelenti, hogy az alapsokaságból valamennyiszer véletlenszerűen kiveszek egy elemet, és a kivett elemet mindig visszateszem. És azt is tudjuk, hogy a reprezentatív minta valószínűsége a legnagyobb, mint a visszatevéses mintavétel esetében, mind a visszatevés nélküli mintavétel esetében. DE!!! Tekintsük a következő példát:
Van 10 darab fehér golyó, 20 darab világosszürke golyó, 30 darab sötétszürke golyó, 40 darab fekete golyót. Most úgy készítek egy 50 elemű mintát, hogy kiveszek 5 darab golyót, megnézem ezt az 5 golyót, visszateszem az alapsokaságba, elkeverem az alapsokaságot, megint kiveszek 5 darab golyót,.... ezt 10-szer csinálom meg. Tulajdonképpen ez is visszatevéses mintavétel, csak a mintavétel 5-ösével történik. Ilyenkor milyen összetételű minta a legvalószínűbb, és mennyi ennek a valószínűsége?
|
|
|
| [2177] marcius8 | 2018-02-13 13:18:31 |
 Keresem az \(\displaystyle a_{n+1}=\sqrt{2a_n+3}\), \(\displaystyle a_1=4\) sorozat explicit alakját. Minden segítséget előre is köszönök! Amit tudok, az hogy a sorozat határértéke 3, és szigorúan monoton csökkenő. Tisztelettel: Bertalan Zoltán.
|
|
| [2174] Fálesz Mihály | 2018-02-02 10:07:26 |
 A két példád között különbség van, és a lényeg a kiválasztási axióma szerepe.
A transzcendens számok halmaza egy konkrét, a kiválasztási axióma használata nélkül is jól megadható halmaz. Az \(\displaystyle \mathbb{R}\)-rel való megfelelést sem nehéz kitalálni, ehhez elég az algebrai számok egy felsorolása, de még felsorolás nélkül sem nehéz.
A bázis esetében a nehézség nem a bijekcióval kezdődik, hanem azzal, hogy melyik bázisról van szó a \(\displaystyle 2^{2^{\aleph_0}}\) lehetőség közül. Azt, hogy egyáltalán létezik bázis, a Zorn-lemmából, vagy a kiválasztási axióma valamelyik más ekvivalens formájából szoktuk bizonyítani. Ha mondasz egy konkrét bázist, én majd mondok hozzá egy konkrét bijekciót az \(\displaystyle \mathbb{R}\)-rel... :-)
|
| Előzmény: [2173] marcius8, 2018-02-01 08:25:51 |
|
| [2173] marcius8 | 2018-02-01 08:25:51 |
 Nem is ezzel van a problémám, hogy oda-vissza létezik kölcsönösen egyértelmű megfeleltetés a valós számok halmaza és egy adott kontinuum-számosságú halmaz között. Hanem azzal, hogy egy adott kontinuum-számosságú halmaz és a valós számok halmaza között nem tudok egy konkrét megfeleltetést létesíteni.
Pl. A transzcendens számok kontinuum-számosságú halmazt alkotnak. Adjunk meg konkrétan egy kölcsönösen egyértelmű megfeleltetést a transzcendens számok és a valós számok között.
Pl. Tekintsük a valós számokat mint a racionális számok feletti vektorteret. Ekkor ennek a vektortérnek van bázisrendszere, és ennek a bázisrendszernek az elemszáma kontinuum-számosságú. Adjunk meg egy kölcsönösen egyértelmű megfeleltetést ezen bázisrendszer és a valós számok között.
|
| Előzmény: [2172] Fálesz Mihály, 2018-01-30 22:30:14 |
|
| [2172] Fálesz Mihály | 2018-01-30 22:30:14 |
 Tehát, ha van egy kontinuum számosságú \(\displaystyle K\) halmazunk, akkor van \(\displaystyle f:\mathbb{R}\to K\) bijekció is.
Az \(\displaystyle \mathbb{R}\)-et \(\displaystyle n\) kontinuum számosságú részre osztjuk — mondjuk \(\displaystyle n\) diszjunkt intervallumra: \(\displaystyle \mathbb{R}=R_1\cup\dots\cup R_n\). Ezután részhalmazokat visszaképezzük az eredeti halmazba:
\(\displaystyle K = f(R_1) \cup \ldots \cup f(R_n). \)
|
| Előzmény: [2171] marcius8, 2018-01-30 08:28:08 |
|
|











