| [2256] Kardos | 2021-08-20 17:14:18 |
 Kedves Mindenki!
Ha valaki tudna segíteni ezekben azt megköszönném :)
|
 |
|
|
|
|
| [2252] marcius8 | 2021-05-02 14:43:27 |
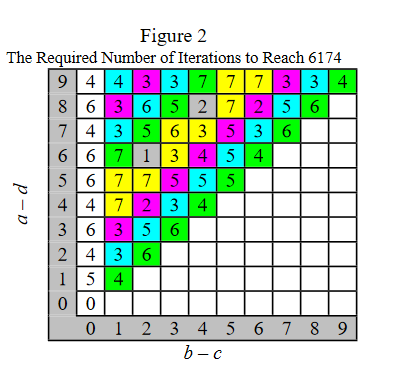
 De tudna valaki arra szükséges és elégséges feltételt mondani, hogy egy négyjegyű számból kiindulva, hogy pontosan a \(\displaystyle k\)-ik iterációt múlva lesz először a kapott eredmény 6174, ahol \(\displaystyle k=1, 2, 3, 4, 5, 6, 7\)?
|
|
| [2251] marcius8 | 2021-05-02 13:27:22 |
 Az \(\displaystyle aaab\) alakú számok esetében, ahol \(\displaystyle a\) és \(\displaystyle b\) különbsége 1, az első kapott eredmény 999 lesz csakugyan. Hogy az iterációt továbbra is a négyjegyű számok körében vigyem végig, ekkor az eredményt 0999-nek veszem, így eljutok a 6174-hez előbb vagy utóbb. De érdekes esetet említettél meg Erzsi, ezt úgy elfelejtettem megvizsgálni.
|
| Előzmény: [2249] Berko Erzsebet, 2021-05-01 02:35:52 |
|
| [2250] Berko Erzsebet | 2021-05-01 06:14:15 |
 Interneten nézelődve, azt javasolják ilyen esetben (9998, 7778), hogy vegyünk hozzá egy 0-t, és működik.
Itt olvashatsz erről a problémáról:
https://plus.maths.org/content/mysterious-number-6174
|
|
| [2249] Berko Erzsebet | 2021-05-01 02:35:52 |
 Többször kaptam a következő számot: 6174. Ha a 6174-ből indulok ki, akkor rögtön 6174-et kapok. Írok 2 számot, ahol a 0 fog ismétlődni: 9998, 7778. (A 1111-gyel osztható számoknál is a 0 ismétlődne.)
|
| Előzmény: [2248] marcius8, 2021-04-30 21:08:08 |
|
| [2248] marcius8 | 2021-04-30 21:08:08 |
 Legyen \(\displaystyle abcd\) egy negyjegyű szám, ahol \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) a számjegyet jelentik, és nem mind a négy számjegy egyforma. A számjegyet csökkenő illetve növekvő sorrendben felírva kapunk két négyjegyű számot, majd a kapott nagyobb négyjegyű számból kivonva a kapott kisebb négyjegyű számot egy négyjegyű eredmény adódik. A kapott eredménnyel elvégezzük az előbbi műveletet, majd az így kapott eredménnyel megint elvégezzük az előbbi műveletet, majd a kapott eredménnyel megint elvégezzük az előbbi műveletet.... Stb. Igaz-e, hogy bármilyen nem 1111-el osztható négyjegyű számból kiindulva ez az iteráció mindig ugyanazt az eredményt adja valahonnan kezdve, és ha igen, akkor hányadik iterációtól kezdve lesz mindig ugyanaz az eredmény? Mindenki segítségét előre is köszönöm.
|
|
| [2247] jsmit654 | 2021-04-28 12:21:42 |
 Azt honnan lehet tudni, hogy egy integral elemi eszkozokkel nem fejezheto ki? Pl. az ellipszis kerulete.
|
|
|
|
| [2244] Lpont | 2021-04-21 16:01:54 |
 Valóban, a KH-nak van 102 és 104 kezdetű azonosítója, sőt a CIB-nek is létezik 107 és 111 kezdetű bankszámlaszáma, és az Erste-t elírtam, helyesen 116.
Bár ezek után a fene se érti...........
|
| Előzmény: [2243] Berko Erzsebet, 2021-04-21 04:10:05 |
|
| [2243] Berko Erzsebet | 2021-04-21 04:10:05 |
 Én is hasonló témával foglalkozom mostanság. Egy összeget kellett befizetnem, átutalnom. Megkaptam a számlaszámot. A neten utánanéztem a banknak. Hogy olcsóbb legyen, oda mentem: KH. (Remélem, így is van.) Azért írok, mert KH, és nem 104-gyel kezdődik, hanem 102-vel.
|
|
|
| [2241] Lpont | 2021-04-20 12:25:42 |
 Még egyszerűbb az azonosítás: az első három számjegy a bankot (pl. OTP:117, KH:104, Erste:106, CIB:107), a következő négy számjegy a fiókot azonosítja, a 8. számjegy az ellenőrző szám.
A 9-16 vagy 9-24 számjegyek az ügyfelet azonosítják, míg a 16. vagy 24. szintén ellenőrző szám.
|
| Előzmény: [2240] Erben Péter, 2021-04-20 07:42:05 |
|
| [2240] Erben Péter | 2021-04-20 07:42:05 |
 Ez az oldal azt mondja, hogy 24-jegyű számlaszámoknál csak két ellenörző kód van (ami úgy működik, ahogy írtad), az első 7 jegy után egy, majd a következő 15 jegy után a második.
Így nekem az jött ki, hogy a három felsorolt szám tényleg helyes. Egy online kereső meg is mondja (az első 8 jegy alapján), hogy melyik bankokról van szó.
|
| Előzmény: [2239] marcius8, 2021-04-17 18:29:49 |
|
| [2239] marcius8 | 2021-04-17 18:29:49 |
 Hátha van itt olyan valaki, aki banki dolgokban járatos. Szóval a bankszámlaszámok 2 vagy 3 darab 8jegyű számból állnak. Én úgy tudom, hogyha egy ilyen 8jegyű szám \(\displaystyle abcdefgh\) alakú, akkor a következő mennyiségnek 0-ra kell végződnie:
\(\displaystyle 9a+7b+3c+1d+9e+7f+3g+1h\)
Tekinthetnénk ezt egy bankszámlaszám érvényességét eldöntő algoritmus ak is. Igen ám, csakhogy találkoztam olyan számlaszámokkal, ahol az azokban lévő 8jegyű számokra az előbbi összefüggés nem teljesül, ugyanakkor internetes oldalon, ahol lehet számlaszámok érvényességét ellenőrizni, az a jelzés érkezik, hogy ezek a számlaszámok érvényesek, technikailag helyesek, pénzcorgalom is van rajtuk, de nem biztos, hogy bankszámlaszámok. Ilyen számok a következők:
10402623-82484855-48511029
10400061-86768370-86551002
10300002-13210936-00014905
Ezek után, ha ezek a számlaszámok nem bankszámlaszámok, akkor milyen számok? Illetve egy bankszámlaszámól hogyan lehet eldönteni, hogy érvényes, ha az általam említett ellenőrzési algoritmus nem jó?
|
|
| [2238] nadorp | 2020-07-20 09:17:40 |
 Nem gondolom,hogy ez Neked "Valaki mondja meg" téma, inkább "Híres(?) álbizonyítások" közé való. Az \(\displaystyle x^3=1\) egyenletig nincs is baj, de ennek 3 gyöke van a komplex számok között, míg az eredi egyenletnek - másodfokú lévén - csak kettő, ráadásul mindkettő harmadik komplex egységgyök. A "bizonyításod" csak arról szól, hogy a valós számok halmazán nincs az eredeti egyenletednek gyöke. Nem a 3=0 azonosságot bizonyítottad be, hanem ellentmondásra jutottál azzal a feltevéssel, hogy a másodfokú egyenletnek van valós gyöke.
|
| Előzmény: [2237] marcius8, 2020-07-16 14:54:39 |
|
| [2237] marcius8 | 2020-07-16 14:54:39 |
 Tétel: \(\displaystyle 3=0\)
Bizonyítás: Megoldandó a következő egyenlet:
\(\displaystyle x^2+x+1=0\)
1. MÓDSZER:
A megoldandó egyenlet mindkét oldalából elvéve \(\displaystyle x\)-et és \(\displaystyle 1\)-et:
\(\displaystyle x^2=−x−1\)
2. MÓDSZER:
A megoldandó egyenlet mindkét oldalát \(\displaystyle x\)-el osztva, ugyanis biztos, hogy \(\displaystyle x\) értéke nem lehet \(\displaystyle 0\):
\(\displaystyle x+1+\frac{1}{x}=0\)
Mindkét oldalból elvéve \(\displaystyle x\)-et és \(\displaystyle 1\)-et:
\(\displaystyle \frac{1}{x}=−x−1\)
ÖSSZEGZÉS: Tehát a megoldandó egyenletből kiindulva két olyan egyenlet adódott a két módszer során, amelyek jobb oldalán ugyanaz az \(\displaystyle −x−1\) kifejezés szerepel, így ennek a két egyenletnek a bal oldala is egyenlő, azaz:
\(\displaystyle x^2=\frac{1}{x}\)
Szorozva \(\displaystyle x\)-el ennek az egyenletnek mindkét oldalát:
\(\displaystyle x^3=1\)
Mindkét oldalból köbgyököt vonva:
\(\displaystyle x=1\)
Behelyettesítve a megoldandó egyenletbe az \(\displaystyle x=1\) kapott értéket:
\(\displaystyle 1^2+1+1=0\)
összevonás:
\(\displaystyle 3=0\)
|
|
| [2234] marcius8 | 2020-03-23 22:00:57 |
 Útmutatás: Ha ábrázolod az \(\displaystyle f_0(x)\), \(\displaystyle f_1(x)\), \(\displaystyle f_2(x)\), \(\displaystyle f_3(x)\), \(\displaystyle f_4(x)\), \(\displaystyle f_5(x)\), ..... függvényeket, észreveszed, hogy a grafikonok milyen szabályosság szerint követik egymást.
|
| Előzmény: [2232] jsmit654, 2020-03-15 12:19:06 |
|
| [2232] jsmit654 | 2020-03-15 12:19:06 |
 \(\displaystyle f_0(x)=|x|, f_n(x)=|f_{n-1}(x)-1|, f_{22221}(22221.1)=?\)
|
|
| [2231] nadorp | 2020-02-29 23:30:51 |
 Ha már integráltunk,akkor deriváljunk is. Az alábbi megoldás egy kicsit számolósab ("ijesztőbb" :-), direktben megadja az \(\displaystyle X=\max_iX_i\) valószínűségi változó eloszlását és ennek generátorfüggvénye alapján számoljuk a várható értéket.
Szükség lesz az \(\displaystyle f(x)=\prod_{i=1}^{n}(e^{p_ix}-1)\) függvény alábbi tulajdonságaira:
\(\displaystyle f{'}(x)-f(x)=\sum_{i=1}^np_i\prod_{j\neq i}(e^{p_jx}-1)\tag1\)
Ha f(x) Taylor-sora \(\displaystyle f(x)=\sum_{k=0}^\infty a_kx^k\), akkor mivel 0 n-szeres gyöke f-nek
\(\displaystyle a_0=...=a_{n-1}=0 \tag2\)
\(\displaystyle f{'}(x)-f(x)=\sum_{k=n}^\infty(ka_{k}-a_{k-1})x^{k-1} \tag3\)
Legyen \(\displaystyle q_k=P(X=k)\). Ekkor nyilván \(\displaystyle q_0=...=q_{n-1}=0\) továbbá a \(\displaystyle G(x)=\sum_{k=n}^\infty q_kx^k\) generátorfüggvény felhasználásával \(\displaystyle E(X)=G{'}(1)\), így elég G'(1) értékét meghatározni.
Ha X=k és utoljára az i értéket húztuk, továbbá a többi j érték \(\displaystyle x_j\)-szer fordult elő (\(\displaystyle x_j\geq1,j\neq i\)), akkor ez az esemény \(\displaystyle \frac{(k-1)!}{\prod{x_j!}}\) esetben fordul elő és minden előfordulás valószínűsége \(\displaystyle p_i\prod p_j^{x_j}\) Tehát
\(\displaystyle q_k=\sum_{i=1}^{n}
\sum_{\begin{matrix} \sum x_j=k-1\\
j\neq i\\
x_j\geq1
\end{matrix}}
p_i\prod p_j^{x_j}\frac{(k-1)!}{\prod {x_j!}}=(k-1)!\sum_{i=1}^{n}p_i
\sum_{\begin{matrix}
\sum x_j=k-1\\
j\neq i\\
x_j\geq1
\end{matrix}}
\prod\frac{p_j^{x_j}}{{x_j!}}\)
Látható, hogy \(\displaystyle \frac{q_k}{(k-1)!}\) értéke megegyezik az (1) jobb oldalán szereplő függvény Taylor-sorában az \(\displaystyle x^{k-1}\) tag együtthatójával, így (3) szerint
\(\displaystyle q_k=(k-1)!(ka_k-a_{k-1})=k!a_k-(k-1)!a_{k-1}=f^{(k)}(0)-f^{(k-1)}(0) \tag4\)
Ha \(\displaystyle F(x)=\sum_{k=n}^\infty f^{(k)}(0)x^k\) (a definíció érvényes |x|<1 esetben, hiszen \(\displaystyle \lim_{k\to\infty} f^{(k)}(0)=\sum q_k=1\)), akkor (4) alapján \(\displaystyle G(x)=F(x)(1-x)\). De \(\displaystyle f^{(k)}(0)\) könnyen számolható, ha f(x) definíciójában elvégezzük a tagonkénti szorzást.
Legyen \(\displaystyle S_i\) a \(\displaystyle \{p_1,...,p_n\}\) halmaz i elemű részhalmazainak a halmaza és tetszőleges \(\displaystyle S\in S_i\) esetén legyen \(\displaystyle |S|=\sum_{p_i\in S}p_i\). Ekkor \(\displaystyle k\geq1\) esetén
\(\displaystyle f^{(k)}(0)=1-\sum_{S\in S_{n-1}}|S|^k+
\sum_{S\in S_{n-2}}|S|^k-...+(-1)^{n-1}\sum_{S\in S_1}|S|^k=1+\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}|S|^k \tag5\)
Felhasználva, hogy (5)-ben mindenhol |S|<1, F(x) hatványsorában |S|x hányadosú mértani sorokat kell összegeznünk, így
\(\displaystyle F(x)=\frac{x^n}{1-x}+\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}\frac{|S|^nx^n}{1-|S|x}\)
\(\displaystyle G(x)=x^n+(1-x)\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}\frac{|S|^nx^n}{1-|S|x}\)
\(\displaystyle E(X)=G{'}(1)=n-\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}\frac{|S|^n}{1-|S|}=n-\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}\left(\frac{|S|^n-1}{1-|S|}+\frac1{1-|S|}\right)\)
Felhasználva, hogy ha \(\displaystyle S\in S_i\), akkor egyértelműen megfeleltethető neki egy olyan \(\displaystyle S'\in S_{n-i}\), hogy 1-|S|=|S'|, kapjuk
\(\displaystyle E(X)=n-\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}\frac{|S|^n-1}{1-|S|}-\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_{n-i}}\frac1{|S|}\)
\(\displaystyle E(X)=n+\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}(|S|^{n-1}+|S|^{n-2}+...+1)+\sum_{i=1}^{n-1}(-1)^{i+1}\sum_{S\in S_i}\frac1{|S|} \tag6\)
Alkalmazzuk most (5)-öt a k=1,2,...n-1 esetben és adjuk össze az egyenlőségeket. Mivel most \(\displaystyle f^{(k)}(0)=0\), kapjuk
\(\displaystyle 0=\sum_{k=1}^{n-1}f^{(k)}(0)=n-1+\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}(|S|^{n-1}+|S|^{n-2}+...+|S|)\)
Ebből azonnal következik, hogy (6)-ban
\(\displaystyle n+\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}(|S|^{n-1}+|S|^{n-2}+...+1)=1+\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}1=1+\sum_{i=1}^{n-1}(-1)^{n-i}\binom{n}{i}=(-1)^{n+1}\)
Tehát
\(\displaystyle E(X)=(-1)^{n+1}+\sum_{i=1}^{n-1}(-1)^{i+1}\sum_{S\in S_i}\frac1{|S|}=\sum_{i=1}^{n}(-1)^{i+1}\sum_{S\in S_i}\frac1{|S|}\)
|
| Előzmény: [2230] Erben Péter, 2020-02-28 09:46:35 |
|
| [2230] Erben Péter | 2020-02-28 09:46:35 |
 Meglepő és szép ez az integrálos átírás. Ha jól látom, két kevésbé közismert összegzési formula is kijön belőle, ha az eredeti szummás alakba behelyettesítjük az \(\displaystyle \frac{1}{n}\) és \(\displaystyle \frac{2}{n}\) valószínűségeket.
Amikor minden valószínűség egyenlő:
\(\displaystyle E = \sum _{k=1}^{n} (-1)^{k+1} \binom{n}{k} \cdot \frac{n}{k} = n\cdot\left(1+\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{n}\right)\)
Innen:
\(\displaystyle \sum _{k=1}^{n} (-1)^{k+1} \binom{n}{k} \cdot \frac{1}{k} = 1+\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{n}\)
A második esetben pedig két részre bontható az összeg. Az első rész megfelel az előző esetnek (\(\displaystyle n-2\) taggal), így a második tagok összegére kapunk összefüggést.
\(\displaystyle E = \sum _{k=1}^{n} (-1)^{k+1} \left(\binom{n-2}{k} \cdot \frac{n}{k} + \binom{n-2}{k-1} \cdot \frac{n}{k+1}\right)= n\cdot\left(1+\frac{1}{2}+\frac{1}{3}+\dots+\frac{1}{n-1} - \frac{1}{n}\right)\)
Áttérve \(\displaystyle n-2\)-ről \(\displaystyle n\)-re és a zárójelek első tagjait a korábbi képlettel összegezve innen azt kapjuk, hogy
\(\displaystyle \sum _{k=0}^{n} (-1)^{k} \binom{n}{k} \cdot \frac{1}{k+2}= \frac{1}{n+1} - \frac{1}{n+2}\)
|
| Előzmény: [2229] Fálesz Mihály, 2020-02-26 11:00:58 |
|
| [2229] Fálesz Mihály | 2020-02-26 11:00:58 |
 A [2224]-beli képletnek van egy vicces átírása integrálokkal:
\(\displaystyle
\sum_i\frac1{p_i}-\sum_{i<j}\frac1{p_i+p_j}+\sum_{i<j<k}\frac1{p_i+p_j+p_k}-+\ldots+(-1)^{n-1}\frac1{p_1+\ldots+p_n} =
\)
\(\displaystyle
= \int_0^1 \left(
\sum_i x^{p_i-1} -\sum_{i<j} x^{p_i+p_j-1}
+\sum_{i<j<k} x^{p_i+p_j+p_k-1}
-+\ldots+(-1)^{n-1}x^{p_1+\ldots+p_n-1}
\right)\mathrm{d}x =
\)
\(\displaystyle
= \int_0^1 \left(1-\prod_{i=1}^n(1-x^{p_i})\right) \frac{\mathrm{d}x}{x}.
\)
Ha \(\displaystyle p_1=\ldots=p_n=\frac1n\), akkor az \(\displaystyle x=(1-y)^n\) helyettesítéssel
\(\displaystyle
\ldots = n\int_0^1 \frac{1-y^n}{1-y} \mathrm{d}y
= n\int_0^1\big(1+y+y^2+\ldots+y^{n-1}\big) \mathrm{d}y
= n\bigg(1+\frac12+\frac13+\ldots+\frac1n\bigg).
\)
Ha csak \(\displaystyle n-1\) valószínűség van, \(\displaystyle p_1=\ldots=p_{n-2}=\frac1n\) és \(\displaystyle p_{n-1}=\frac2n\), akkor, ugyanazzal a helyettesítéssel
\(\displaystyle
...
= n\int_0^1 \frac{\big(1-y^{n-2}(2y-y^2)\big)}{1-y} \mathrm{d}y
= n\int_0^1\big(1+y+y^2+\ldots+y^{n-2}-y^{n-1}\big) \mathrm{d}y =
\)
\(\displaystyle
= n\bigg(1+\frac12+\frac13+\ldots+\frac1{n-1}-\frac1n\bigg).
\)
Ebből is leolvasható, hogy a különbség éppen \(\displaystyle 2\).
(jonas [2227]-ből is látszik, egyszerűbben és kevésbé ijesztően.)
|
| Előzmény: [2228] Erben Péter, 2020-02-25 17:52:37 |
|