| [225] pvong17 | 2007-07-04 21:03:34 |
 Üdv, gondoltam gyakorolgatok nyáron egy kicsit az érettségire, de máris akadt egy feladat, ahol megakadtam. Nem akarom senkinek az idejét rabolni ezzel, mert gondolom itt nem ilyen feladatok az " érdekesek ". Lehet már kezdek vakulni, hogy nem látok meg benne egy alapvető azonosságot ..:) , de már nem tudok kit kérdezni. Aki veszi a "fáradságot" ,előre is köszönöm !
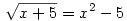
|
|
|
| [223] jonas | 2007-06-30 23:01:05 |
 Nem, tévedtem. 1000000 van, és nyolc megoldhatatlan köztük.
|
|
|
| [221] SAMBUCA | 2007-06-30 18:17:28 |
 Elég népszerű mostanában a freecell, vannak netes változatok is, meg szép számmal fórumok is. Nem minden leosztás oldható meg, ha jól tudom a következők nem: 11982, 146692, 186216, 455889, 495505, 512118, 517776, 781948
SAMBUCA
|
|
| [220] lorantfy | 2007-06-30 17:01:38 |
 Értettem a kérdésedet. Én most játszottam először ezzel a játékkal (nem is rossz!) Nekem a játék kiválasztása menüpontnál 1-1.000.000 lehetőséget ír ki. (Érdekes, hogy a -1, -2 értékeket is megengedi). Bár nekem jópárszor nem sikerült megoldani egy-egy játékot, arra gondolok, hogy ez az 1.000.000 játék megoldható.
Mivel az adott feladatszámhoz mindig ugyanaz a kiosztás jön ki, tehát nem véletlenszerű leosztást kapunk.
Szerintem a kész állapotból számítógépes programmal visszafelé állították elő azeket a kiosztásokat.
Tegyük fel, hogy összeraktuk a 4 paklit jobboldalon. Most a baloldali 4 mező használata nélkül egyszerűen rakjuk vissza a lapokat az oszlopokba. Ezek biztosan (és könnyen) megoldható kiosztások lesznek. Nézzük, hány ilyen van.
Minden lap kirakásakor 4 közül választhatunk és berakjuk valamelyik oszlopba. Az utolsó sor kivételével 8 oszlop közül választhatunk, az utolsó sorban marad 4.
Ez az első 13 lap lerakásáig így megy, aztán esetleg elfogyhat egyik pakli, úgyhogy bonyolódik a helyzet.
Mindenesetre az első 13 lap visszarakása már : (4.8)13=3,7.1019 eset, becsüljök a továbbiakat:(3.8)13 majd (2.8)13 és végül (1.8)9.44-al. Erre nekem 5.1063-re jött ki. Ezek lennének a könnyedén megoldható leosztások. Ez túl soknak tűnik az előző szához képest, tehát lehet, hogy valahol tévedek.
|
| Előzmény: [219] Anzelmus, 2007-06-30 15:17:23 |
|
| [219] Anzelmus | 2007-06-30 15:17:23 |
 Csak a program kínál 100000 lapleosztást; a valóságban persze, hogy több van.
A kérdésem -ami lehet, hogy nem volt teljesen jól megfogalmazva- azonban az volt, hogy a (10 a 65.-en) [elnézést, még nem ismerem a TeX-et] db esetből vajon mennyi az, amit a játék szabályai szerint képtelenség megoldani. (Pl. a játékszámként beírt -2 vagy -1 esetében is érzésem szerint megoldhatatlan leosztást kapunk.)
.
|
| Előzmény: [218] lorantfy, 2007-06-30 12:00:05 |
|
| [218] lorantfy | 2007-06-30 12:00:05 |
 Szia Anzelmus!
Honnan veszed, hogy 100000 lapleosztás van?
4 db 7-es oszlop van, ezek felcserélhetők egymással. 4 db 6-os oszlop van ezek is felcserélhetők. Az oszlopokon belül számít a sorrend.
Az 52 kártyából az első 7-es oszlop lapjainak kiválasztására: 52x51x50x49x48x47x46 féle lehetőség van.
A következő 7-es oszlop: 45x44x43x42x41x40x39 lehetőség...
Az utolsó 6-os oszlop: 6x5x4x3x2x1
Vagyis eddig: 52! eset. Ezt a megfelelő oszlopok felcserélése miatt: 4!x4!-al kell leosztani.
Az esetek száma: 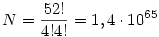
|
| Előzmény: [217] Anzelmus, 2007-06-29 21:21:13 |
|
| [217] Anzelmus | 2007-06-29 21:21:13 |
 Sziasztok.
Bizonyára jónéhányan ismeritek a Windowsból az Admirális (Freecell) c. kártyajátékot. A 100 000 különböző játéklehetőség (az egymástól eltérő játszmák száma) igen soknak tűmik, és sejthető, hogy nem minden lapleosztás oldahtó meg. Mennyire nehéz ezt -egy ilyen összetettségű- feladatot, ill. a bizonyítást matematikai formába önteni?
|
|
| [216] Lóczi Lajos | 2007-06-28 14:24:56 |
 Azért bőbeszédű az idézet, mert, ahogyan Sirpi is említette, a lineáris szónak nem teljesen egyértelmű a jelentése: egy valós-valós függvényt akkor is lineárisnak mondunk, ha nem homogén, vagyis b 0, de a lineáris algebrában vagy funkcionálanalízisben ez már nincs így. 0, de a lineáris algebrában vagy funkcionálanalízisben ez már nincs így.
|
| Előzmény: [215] farkasroka, 2007-06-28 12:14:03 |
|
| [215] farkasroka | 2007-06-28 12:14:03 |
 Sziasztok!
Azóta egy ismerősöm felvilágosított, hogy ha a tenzorokat mélyebben meg szeretném ismerni akkor a multilineáris algebrát kell elővennem, mint ahogy Lóczi Lajos utalt rá. Ilymódon a tenzor pontos matematikai definíciójára egyenlőre nem vagyok kíváncsi. Viszont annál inkább arra, hogy miképpen kellene értelmezni a tenzorok következő bevezetését (sallangok nélkül): "Egy A operátort lineáris operátornak nevezünk, ha additív: A(x+y)=Ax+Ay és homogén:A(ax)=aA(x) bármely x,y,a-ra. A tenzorok lineáris ÉS homogén operátorok..." Az idézet nem volt pontos.
Gondolhatnánk arra, hogy a tenzorok lineáris operátorok és a mátrixuk mindig megfelel egy lineáris és homogén egyenletrendszer(vagy transzformáció) mátrixának de ez akkor is sántít. Lehet,hogy egyszerűen keverve vannak a fogalmi apparátusok és akkor nincs kérdés.De ha nem akkor mit takar ebben a környezetben az, hogy "lineáris ÉS homogén"?
Mondhatná valaki, hogy szőrözök, de az az igazság, hogy amikor tenzorokra haználtam az említett kifejezést majdnem kivágtak a teremből.(persze matekon)
|
|
| [214] Lóczi Lajos | 2007-06-26 13:43:31 |
 Szoktak lineárisnak nevezni leképezéseket akkor is, ha teljesítik az additivitási és homogenitási függvényegyenleteket; ilyen szövegkörnyezetben az említett példádat affin lineárisnak hívjuk a B 0 esetben. 0 esetben.
A tenzorokra sokszor célszerű multilineáris leképezésekként gondolnunk.
|
| Előzmény: [213] Sirpi, 2007-06-26 13:28:54 |
|
|
| [212] farkasroka | 2007-06-26 11:26:31 |
 Sziasztok!
Valaki mondja már meg mi a pontos matematikai definíciója a fizikában használt tenzoroknak? Valamennyi általam fellelt definícióban szerepel a "lineáris és homogén" jelző. Ha valami lineáris akkor homogén és additív. Tehát az lenne a kérdésem, hogy mire utal ez az extra homogén jelző.
Előre is köszönöm!
|
|
|
|
| [209] gdoki | 2007-06-23 00:45:44 |
 Bocsi, nem tudtam, hogy Tex-el is lehet...ha a kép nem jelenne meg...
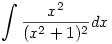 -re -re
kéne a megoldás, pontosabban annak menete...mert érdekel a miként! Köszönöm előre is mégegyszer!
|
| Előzmény: [208] gdoki, 2007-06-23 00:26:11 |
|
| [208] gdoki | 2007-06-23 00:26:11 |
 Hi bárki!
Főiskolás volnék és nagyon elhanyagoltam a matekot...most szeretném bepótolni, csak rövid az időm az alábbi feladatra. Válaszokat előre is köszönöm!
|
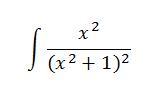 |
|
|
|
| [205] farkasroka | 2007-06-13 17:22:43 |
 Sziasztok!
Azt szeretném tudni, hogyan lehet az 1/x függvény folytonosságát bizonyítani közvetlenül a definícióból, pontosabban hogyan függ a delta az epszilontól a szokásos jelölésekkel?
Elnézést a triviális kérdésért, segítségeteket előre is köszönöm!
|
|
|
| [203] Csimby | 2007-05-23 01:22:00 |
 Zn az n rendű ciklikus csoport. Zn×Zk pedig ezek direkt-szorzata, úgy képzeld el, hogy minden elemnek van két koordinátája és a csoport művelet az elsőkoordinátán Zn-ből a másodikon Zk-ból öröklődik. Tehát (a,b) összeműveletezve (c,d)-vel egyenlő (a+c,b+d)-vel ahol a-t és c-t Zn-ben adtuk össze, b-t és d-t pedig Zk-ban. Könnyen látható hogy ez csoport és rendje nk. (Zn-re gondolhatunk úgy mint a modulo n maradékosztályokra az összeadásra nézve, és mivel Abel-csoport, ezért írtam "+"-val a műveletet, ekkor az egység elem a 0, a generátor elem (ami önmagával összeműveletezve kiadja az egész csoportot) pedig az 1). Már csak azt kell meggondolni, hogy Z27×Z3-ban (1,0) rendje tényleg 27, vagyis (1,0)+...+(1,0) (27-szer összeadva) tényleg egyenlő (0,0)-val. És hogy Z27×Z3 nem ciklikus (vigyázat pl. Z4×Z3 ciklikus). De mondjuk más ellenpélda is lehetséges, mivel g29=g2 akkor is teljesül pl. ha g3=1 vagy g9=1. Vagy esetleg g maga az egységelem.
|
| Előzmény: [202] phantom_of_the_opera, 2007-05-22 22:40:03 |
|
|
| [201] Csimby | 2007-05-22 22:18:03 |
 g29=g2-ből g27=1. A 81 rendű csoport lehet akár Z27×Z3, amiben van 27-rendű elem pl. (1,0) ahol 1 Z27 generátoreleme, 0 pedig Z3 egységeleme. De ez a csoport nem ciklikus. Remélem nem írtam hülyeséget.
|
| Előzmény: [200] phantom_of_the_opera, 2007-05-22 11:18:59 |
|








 0, de a lineáris algebrában vagy funkcionálanalízisben ez már nincs így.
0, de a lineáris algebrában vagy funkcionálanalízisben ez már nincs így. 

 Ax+B. Akkor homogén, ha 0
Ax+B. Akkor homogén, ha 0
 '
'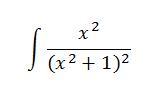
 >0 rögzített. Legyen
>0 rögzített. Legyen  egyelőre olyan, hogy
egyelőre olyan, hogy  |x0|/2. Legyen x tetszőleges olyan, hogy |x-x0|<
|x0|/2. Legyen x tetszőleges olyan, hogy |x-x0|<
