| [360] epsilon | 2008-03-07 13:31:48 |
 Bocs a [-3,-3] elgépelés helyette [-3,-2]
|
|
| [359] epsilon | 2008-03-07 13:29:17 |
 A hozzáfűznivalóim:
(131) Én arra gondoltam, hogy a nevezőnek ne legyenek valós gyökei, így a d<o ahonnan m a (0,4) intervallumhoz tartozik. A megadott helyes (?) válasz: más válasz (még választhatók voltak: R, 4, -1, (0,4).
(117) Sima számolásokkal kijött, hogy e=0, és ez (-1,1) között van. A megadott helyes (?) válsz: nem létezik semleges elem.
(277) Az x+y összeget S-el, az xy szorzatot P-vel jelöltem, és pl. ha az alsó 2 egyenletet megoldom, és a megoldás kell teljesítse az első egyenletet, akkor sem kapok intervallumot, és a helyes megoldás: [-3,-3]
Nektek mi a véleményetek? Előre is kösz, üdv: epsilon
|
|
|
|
| [356] epsilon | 2008-03-07 13:26:44 |
 Helló! Újra jelentkezem, mert vagy elromlott a humorom, vagy mészlerakódásom van...vagy hibás a "helyes válasz"? Íme a feladatok:
|
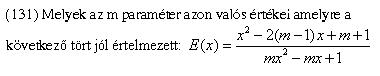 |
|
| [355] epsilon | 2008-03-06 13:56:02 |
 Köszi Lajos! Így már semmi kétség nem fér hozzá! Üdv: epsilon
|
|
| [354] Lóczi Lajos | 2008-03-06 12:16:53 |
 Azért, mert e- kitevőjében lényegében az első k szám összege szerepel, ami nagyságrendileg k2/2, az alacsonyabb rendű tagok a limeszben eltűnnek. Ha ebből k2-edik gyököt vonsz, 1/2 marad. kitevőjében lényegében az első k szám összege szerepel, ami nagyságrendileg k2/2, az alacsonyabb rendű tagok a limeszben eltűnnek. Ha ebből k2-edik gyököt vonsz, 1/2 marad.
|
| Előzmény: [353] epsilon, 2008-03-06 06:43:23 |
|
| [353] epsilon | 2008-03-06 06:43:23 |
 Helló Lajos! A megoldásodat még alaposan át kell sasoljam, mert addig értem, amíg a fogóba behelyezed, aztán látható, hogy az n a második hatványon kitevőt n×n-re lehet bontani, de azt nem értem, hogy a végén ahol megint n-edik gyök lenne, miért lett helyette éppen négyzetgyök? Hiszen eleinte olysami volt a bal oldalon pl. hogy (e-epsilon) az n-edik hatványon, de ha ebből n×n-edik gyököt vonok, hogyan lenne négyzetgyök??? A részleges határértékre térést értem, éppen ezen gondolkodtam el amikor megláttam, hogy Te is előbb csak n-edik gyököt vonsz, arra gondoltam, hogy még a hátramaradt n-edik gyökvonás ugyanazt jelenti, de mintha mégis másképpen kerülted ki. Üdv: epsilon
|
| Előzmény: [349] Lóczi Lajos, 2008-03-05 13:57:32 |
|
| [352] epsilon | 2008-03-05 20:21:18 |
 OK cauchy, Én éppen félreértettelek, azt hittem, hogy amellett tartasz ki a 346-ban, hogy a feladatban OK az alulról húzott érintő (tehát alatta van), és konvex a (0,1)-en amit beláttunk, hogy nem igaz, holott figyelmetlenségem miatt elsiklottam afölött, hogy azt hangsúlyoztad ki, hogy az érintős definició sem mondott csődöt, szóval ennek örvendek, mert kezdett meginogni bennem, hogy amit sok éve tanítottak, most miért állna a fejére? De most már a szép esztétikus rajzod alapján is megnyugodtam ;-)
|
|
|
| [350] epsilon | 2008-03-05 16:10:49 |
 Nem, éppen azt igazoltam a rajzon is amit láthatsz, hogy az érintők helyett az a=1/2-ben csak bal és jobboldali érintők vannak (egy szögponttal van dolgunk, ahol a kél szélső derivált különböző de véges), ellenben mint olvashatod, a függvény azon a értékekre amelyekre (0,1) intervallumban vannak NEM KONVEX (Én is igazoltam, hogy kijön a konvexitás). Tehát az érintők alúl vannak és mégsem konvex? Tehát...???? Szerintem ezért nem helytálló ez a definició!
|
| Előzmény: [345] epsilon, 2008-03-05 10:23:25 |
|
| [349] Lóczi Lajos | 2008-03-05 13:57:32 |
 "1) Írtad, hogy "megmutatjuk", hogy a limesz a végén gyök e, ... Van valami kiegészítésed, hogyan is jön ki pontosan a gyök e, (vagyis a "megmutatjuk" hogyanja)..."
Ez a gondolat ugyanaz, mint a nadorp által [325]-ben felvázolt (csak logaritmusvétel nélkül): az 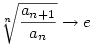 limesz definíciója szerint minden limesz definíciója szerint minden  >0-hoz van olyan N( >0-hoz van olyan N( ), hogy az N-nél nagyobb n-ekre (e- ), hogy az N-nél nagyobb n-ekre (e- )nan<an+1<(e+ )nan<an+1<(e+ )nan. Ebből rekurzívan felírsz egy közrefogást aN+k-ra (k tetszőleges természetes szám), majd e )nan. Ebből rekurzívan felírsz egy közrefogást aN+k-ra (k tetszőleges természetes szám), majd e  kitevőiben elvégzed az összegzést, így egy kitevőiben elvégzed az összegzést, így egy
(e- )valami.aN<aN+k<(e+ )valami.aN<aN+k<(e+ )valamihasonlo.aN )valamihasonlo.aN
alakú egyenlőtlenséghez jutsz. Most k2-edik gyököt vonunk, a lánc bal és középső tagjában liminf-et veszünk, míg a középső és jobb tagjában limsup-ot, majd kihasználjuk, hogy pl. 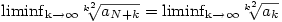 (hiszen N most fix; vagyis a fix indexeltolás nem befolyásolja a liminf/limsup értékét), ebből azt kapjuk, hogy (hiszen N most fix; vagyis a fix indexeltolás nem befolyásolja a liminf/limsup értékét), ebből azt kapjuk, hogy
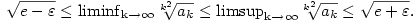
A fenti érvelés viszont minden  >0-ra igaz, emiatt létezik tehát >0-ra igaz, emiatt létezik tehát 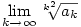 és értéke és értéke 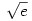 . .
|
| Előzmény: [342] epsilon, 2008-03-05 06:37:26 |
|
| [348] Lóczi Lajos | 2008-03-05 13:38:37 |
 "Ha jól akartam, a 308-nál ugyanezt végeztem, de a parciális határértékretérés gyanúja állt fenn, ott meg a limesz e-nek jött ki."
Általában nem szabad egy részkifejezést a határértékével helyettesíteni, vagy két kifejezést egymással helyetteíteni, mégha a limeszük ugyanaz is, mert akkor fals eredmények jöhetnek ki: ezt tetted a [308]-as végén is, s ezért jött ki rossz eredménynek e a végére.
A fenti manipulációk veszélyességéről rögtön meggyőződsz, ha a hibás

sorra pillantasz, "hiszen 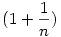 és 1 limesze ugyanaz a végtelenben". és 1 limesze ugyanaz a végtelenben".
|
| Előzmény: [342] epsilon, 2008-03-05 06:37:26 |
|
| [347] Lóczi Lajos | 2008-03-05 12:38:27 |
 Egy "konvexitásdefiníció" annál általánosabb, minél kevesebbet követel meg az f függvényről. Az említett 3 értelmezés közül a legáltalánosabb az, amelyben nincs simasági (azaz deriválhatósági) megkötés: ebben csak a húr szerepel. Ezzel a definícióval igaz, hogy ha f egyszer deriválható, akkor a konvexitás egyenértékű a derivált monoton növekedésével. Továbbá, ha a függvény kétszer deriválható, akkor a konvexitás egyenértékű a második derivált nemnegativitásával.
Ha valaki a konvexitást az első deriválttal akarja definiálni, kevesebb függvényt tudna konvexnek mondani. Hasonlóan, ha a második derivált lenne a definícióban, még tovább szűkülne a "konvex függvény" fogalma.
Mindazonáltal igaz az a tétel, hogy egy -- intervallumon értelmezett és a húros definíció értelmében -- konvex függvény (Lebesgue-) majdnem mindenütt deriválható, sőt, egy megszámlálható halmaz kivételével mindenütt deriválható.
|
| Előzmény: [346] cauchy, 2008-03-05 12:02:50 |
|
|
| [345] epsilon | 2008-03-05 10:23:25 |
 Valóban, a másodrendű deriváltat Én is csak tételként használom, noha láttam könyvet ahol definició, de mi régen az érintős definiciót tanultuk, és még mindig sok helyen így tanítják, de mint látható, most sem állta a helyét, de a felezőpontos definiciót nem igazán tanítottak, úgyhogy megérte itt erről is hallani ;-)
|
|
| [344] nadorp | 2008-03-05 08:45:21 |
 Én még úgy tanultam, hogy egy függvénygörbe konvex egy [a,b] intervallumon, ha tetszőleges két pontját összekötő szakasz felezőpontja görbe felett (vagy rajta) van.Ha az intervallumon a függvény kétszer deriválható, akkor a második deriváltak nemnegativitása szükséges és elegendő feltétel, de ez már tétel. Esetünkben az eredeti definíció érvényességét tudjuk csak vizsgálni, hiszen a függvény az x=a pontban nem deriválható.
|
| Előzmény: [343] epsilon, 2008-03-05 06:40:40 |
|
| [343] epsilon | 2008-03-05 06:40:40 |
 Igen érdekes elgondolkodni a konvexitás fogalmának a defieálásán, hiszen mint az érintős meghatározás, mint az, hogy f"(x) ne legyen negatív nem igazán fogadható el ezek szerint a konvexitás értelmezésének, mert a derivált belekeverése nem "fair" tehát legtisztább a húrral defineálni és úgy tanítani, noha sok szakkönyvben nem éppen így teszik.
|
| Előzmény: [340] Lóczi Lajos, 2008-03-04 22:07:31 |
|
| [342] epsilon | 2008-03-05 06:37:26 |
 Kedves Lajos! Örvendek, hogy megerősíted ezt a megoldási lehetőséget, a 308-as hozzászólásnál Én is ezt próbáltam bemutatni, Én ugyan a Stolz-Cezaro tétel 3. következménbyeként ismerem, ugyanis azzal levezethető, de Cauchy-D'Alambert tételnek forgalmazzák a Sorok elméletében, a lényeg az lenne, hogy: 1) Írtad, hogy "megmutatjuk", hogy a limesz a végén gyök e, 2) Ha jól akartam, a 308-nál ugyanezt végeztem, de a parciális határértékretérés gyanúja állt fenn, ott meg a limesz e-nek jött ki. Van valami kiegészítésed, hogyan is jön ki pontosan a gyök e, (vagyis a "megmutatjuk" hogyanja) meg miért van ellentmondásba az eredmény a 308-cal, mert nagyon tetszik ez a megoldásod, hiszen a teszt középiskolásoknak szól, így nagyágyúval rálőni nem fair, amit mutattam szerintem az is elég hosszadalmas, szerintem ilyesfélén ahogyan írtad egészen plauzíbilis! Üdv: epsilon
|
|
| [341] Lóczi Lajos | 2008-03-04 22:29:48 |
 Még egyszer hadd térjek vissza a problémára egy utólagos elemzés erejéig, más kiindulással és kevésbé explicit érveléssel, a Stirling-re való hivatkozás nélkül.
A hányados- és gyökkritérium témaköréből ismert a következő egyenlőtlenséglánc:
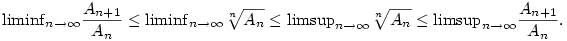
(Ez a lánc egyébként azt mondja, hogy a gyökkritérium erősebb a hányadoskritériumnál.)
A megadott rekurziót az en=(1+1/n)n és 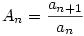 jelölésekkel így írhatjuk át: jelölésekkel így írhatjuk át:
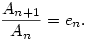
Mivel itt a jobb oldal liminf-je és limsup-ja egyaránt e, a fentiekből rögtön adódik, hogy létezik
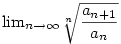
és e-vel egyenlő. Innen a továbbhaladás már hasonló (de logaritmálás nélkül is megy a dolog persze), a limesz definíciójából kiindulva megmutatjuk, hogy létezik
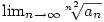
és 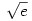 -vel egyenlő. -vel egyenlő.
|
| Előzmény: [325] nadorp, 2008-03-03 21:56:02 |
|
|
| [339] epsilon | 2008-03-04 17:49:25 |
 OK, köszi mindkettőtöknek! Így már tiszta!
|
|
| [338] sakkmath | 2008-03-04 15:48:23 |
 Egyetértőleg csatlakozom az előttem szólóhoz. A 297. feladat szövege nem szól az f függvény [0;1]-beli differenciálhatóságáról, ezért a kovexitás érintős definícióját ne használjuk. A konvexitás kérdésében - tankönyv híján - vegyük a WIKIPÉDIA másik definícióját:
Az f: I  R intervallumon értelmezett valós változójú függvény konvex, ha a függvénygörbe (bármely, az adott intervallumba eső ÿ(kiegészítés tőlem)) két pontját összekötő húr a függvénygörbe fölött halad ... R intervallumon értelmezett valós változójú függvény konvex, ha a függvénygörbe (bármely, az adott intervallumba eső ÿ(kiegészítés tőlem)) két pontját összekötő húr a függvénygörbe fölött halad ...
|
|
|
|



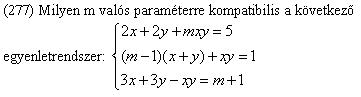
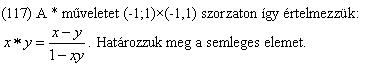
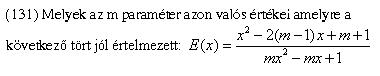

 kitevőjében lényegében az első k szám összege szerepel, ami nagyságrendileg k2/2, az alacsonyabb rendű tagok a limeszben eltűnnek. Ha ebből k2-edik gyököt vonsz, 1/2 marad.
kitevőjében lényegében az első k szám összege szerepel, ami nagyságrendileg k2/2, az alacsonyabb rendű tagok a limeszben eltűnnek. Ha ebből k2-edik gyököt vonsz, 1/2 marad.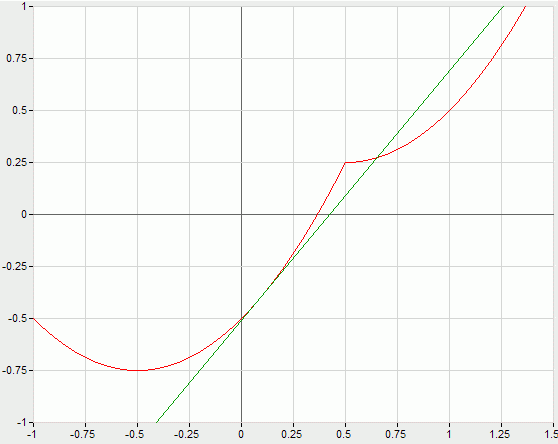


 R intervallumon értelmezett valós változójú függvény konvex, ha a függvénygörbe (bármely, az adott intervallumba eső ÿ(kiegészítés tőlem)) két pontját összekötő húr a függvénygörbe fölött halad ...
R intervallumon értelmezett valós változójú függvény konvex, ha a függvénygörbe (bármely, az adott intervallumba eső ÿ(kiegészítés tőlem)) két pontját összekötő húr a függvénygörbe fölött halad ...