| [412] csewe | 2008-04-04 15:13:47 |
 mindenkinek kösz a segítséget a wikipédiás oldal angol,ugyhogy ez nálam kilőve
a gyökvonásból nemsokat értettem, mert éphogy hármas voltam matekból, és már az sem most volt
mivel ez az egyenlet amire itt megoldást kértem ,csupán a program gyorsítását szolgálta volna, így arra az elhatározásra jutottam, hogy más megoldást keresek
ti jók voltatok, csak ez már nekem magas
sziasztok
|
| Előzmény: [411] Sirpi, 2008-04-04 14:19:18 |
|
|
| [410] Róbert Gida | 2008-04-04 13:58:23 |
 Van egyébként osztásmentes verziója is a négyzetgyök kiszámolásának (ott szorozni kell). Továbbá a legjobb programok természetesen nem teljes pontossággal számolnak, mint te például 14 jeggyel, hanem mindig kb. megduplázzák az értékes jegyek számát az ak-ban.
|
| Előzmény: [409] Sirpi, 2008-04-04 12:42:14 |
|
| [409] Sirpi | 2008-04-04 12:42:14 |
 Ha már felmerült a téma, és azt állítottam, hogy a pontos jegyek száma iterációs lépésenként duplázódik, akkor kicsit pontosítanék, meg bizonyítanám is az állításomat. Tehát a rekurzió 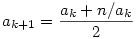
A számtani-mértani közepek közti egyenlőtlenség szerint ez mindig legalább 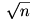 , így tegyük fel, hogy , így tegyük fel, hogy  (tehát x-nek c( (tehát x-nek c( 0) a hibája), és nézzük meg, hogy x-re alkalmazva az iterációt, mekkora lesz a következő tag, azaz 0) a hibája), és nézzük meg, hogy x-re alkalmazva az iterációt, mekkora lesz a következő tag, azaz 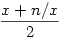 hibája. hibája.
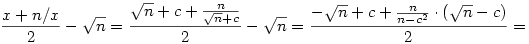
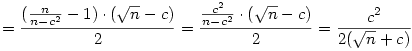
Ebből már pár dolog kiolvasható. Ha x nagy  -hez viszonyítva, akkor a hiba nagyjából feleződik: x=tn, ekkor c is hasonló nagyságrendű, és -hez viszonyítva, akkor a hiba nagyjából feleződik: x=tn, ekkor c is hasonló nagyságrendű, és 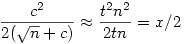
Viszont ha már c<1, akkor a következő hiba már kisebb, mint c2, vagyis valóban igaz a lépésenkénti duplázódó pontosság.
* * *
Ha gyorsítani akarunk az eljáráson, akkor annyit még érdemes megtenni, hogy a  -re adunk egy körülbelüli becslést, hogy az algoritmusnak ne kelljen az n,n/2,n/4... lépéseken végigmennie. Ha d alapú számrendszert használunk, akkor keressük meg a legkisebb k-t, amire n -re adunk egy körülbelüli becslést, hogy az algoritmusnak ne kelljen az n,n/2,n/4... lépéseken végigmennie. Ha d alapú számrendszert használunk, akkor keressük meg a legkisebb k-t, amire n d2k, és ilyenkor indítsuk az algoritmust dk-ból, ezzel az első jó pár lépést megspóroljuk. d2k, és ilyenkor indítsuk az algoritmust dk-ból, ezzel az első jó pár lépést megspóroljuk.
Egy példa a  kiszámolására, a1=2 indulóértékkel: kiszámolására, a1=2 indulóértékkel:
2,00000000000000 --- 1,50000000000000 --- 1,41666666666667 --- 1,41421568627451 --- 1,41421356237469 --- 1,41421356237309 --- 1,41421356237309
Vagyis a 6. érték már 14 jegyre pontos.
|
| Előzmény: [406] Sirpi, 2008-04-03 10:40:19 |
|
| [408] Hajba Károly | 2008-04-04 00:18:51 |
 Hallgass Sirpire, meglásd megéri!
Mivel a Sirpi javasolta rekurziós gyökvonás pontossága hatványozottan nő, így nagy számok esetén is gyors eredményt adhat. Talán nagyobb problémád lesz a nagy számok kezelésével, mint ezzel az eljárással.
|
| Előzmény: [407] csewe, 2008-04-03 14:48:10 |
|
| [407] csewe | 2008-04-03 14:48:10 |
 tulajdonképpen a szummát (remélem jól fogalmazok" szeretném visszafejteni n = (1 + 2 + 3 + 4 + ...végtelen) az egyenlettel megkapom ,hogy hányadik lépésnél éri el az n -et az összedás.
ehhez tudnotok kell hogy az eredeti képletem n = x * (x + 1 ) / 2 volt ezzel a képlettel megkaptam hogy hány számot kell összeadnom ,hony n -hez jussak.
reményeim szerint egy prímszitához tudom majd felhasználni a képletet , amivel néhányszáz esetleg néhányezer digites számokrol mondanám meg hogy prím e
a gyökvonás hosszú időtrabló folyamat, és nekem gyors algoritmus kellene
de sajnos nem ez az egyetlen probléma , hanem a nagy számok programozása is úgyhogy egyenlőre csak akkora számokra írom meg a rutint amekkorát a programnyelv alapból kezelni tud ,és ha sikeres akkor rátérek a nagyobb feladatra
ez nekem csak kedvtelés , de nagyon megköszönném, ha segitenétek.
|
| Előzmény: [406] Sirpi, 2008-04-03 10:40:19 |
|
| [406] Sirpi | 2008-04-03 10:40:19 |
 Igazából mire és milyen környezetben kell Neked erre megoldást adni? Mert amit írtam (a másodfokú egyenlet megoldóképlete szerinti megoldást), az a megoldás, és más nincs, szóval nem lehet gyökjel nélkül felírni. Programmal akarod esetleg csinálni? (Mert ott elvileg van gyökvonás.) Meg milyen nagyságrendű az n? Ha ezekre választ adsz, akkor jobban segíteni tudunk talán abban, amire szükséged van.
* * *
A gyökvonást mi magunk is implementálhatjuk, alapműveletekkel, ha épp nem akarunk beépítettet használni. Legyen mondjuk a1=1 (vagy a 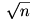 bármilyen közelítése, ha tudunk jobbat), majd bármilyen közelítése, ha tudunk jobbat), majd  . Ez a rekurzió nagyon gyorsan tart a . Ez a rekurzió nagyon gyorsan tart a 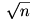 -hez, ak+1-nek kétszer annyi jegye pontos, mint ak-nak. Csak be kell állítani valami leállási paramétert, hogy a program ne fusson a végtelenségig (pl. -hez, ak+1-nek kétszer annyi jegye pontos, mint ak-nak. Csak be kell állítani valami leállási paramétert, hogy a program ne fusson a végtelenségig (pl. 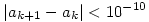 , vagy amilyen pontosság nekünk kell). , vagy amilyen pontosság nekünk kell).
|
| Előzmény: [405] csewe, 2008-04-03 08:42:26 |
|
|
|
| [403] csewe | 2008-04-02 17:50:26 |
 köszi a megoldást
még azt kérdezném,hogy nem menne ez gyökvonás nélkül
mert nagy számoknál ez elég problémás
|
|
|
| [400] csewe | 2008-04-02 17:02:09 |
 sziasztok
meg kellene oldanom ezt az egyenletet
n = x*(x + 1)
n pozitív egész pl:30 , 42 , 50 stb
szeretném megkapni x - et
persze nem ezeknél a kis számoknál okoz gondot a dolog
ha valaki tudja legyenszives vezesse le nekem a megoldást
köszi
|
|
|
| [398] Sirpi | 2008-03-26 16:31:32 |
 A 3.-at annyival egészíteném én ki, hogy mivel a 45 és a 102 lnko-ja 3, ezért azzal rögtön le lehet osztani:
34x+15y=53/3
Vagyis nincs egész megoldás, mert a bal oldal biztos egész, a jobb meg nem.
|
| Előzmény: [396] BohnerGéza, 2008-03-26 10:32:40 |
|
|
|
| [395] Sirpi | 2008-03-25 17:46:59 |
 A 2. és a harmadik ugyanolyan típusú, a 2-esen mutatom meg, hogy megy a dolog. Kell találnod egy megoldást, ilyen pl. az x=4, y=1. Ezt pl. meg lehet úgy tenni, hogy a 19-ből 7-esével lépkedsz lefelé (felfelé), és figyeled, mikor jutsz 3-mal osztható számhoz.
Ha megvan egy megoldás, fel kell használni, hogy ha x és y megoldás, akkor x+7 és y-3 is az, vagyis a megoldások: 4+7k, 1-3k. Behelyettesítve: 3(4+7k)+7(1-3k)=12+21k+7-21k=19, tehát tényleg megoldások.
Az első pedig elég közismert:
xy=x+y
xy-x-y+1=1
(x-1)(y-1)=1
Innen rögtön kijön, hogy tetszőleges x esetén 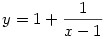 , valósokra ezzel meg is oldottuk a feladatot. Ha azt is feltesszük, hogy mindkettő egész, akkor is könnyű dolgunk van, ugyanis az 1 csak 1.1 és (-1).(-1) alakban bomlik két egész szám szorzatára, innen a megoldások: x=y=0 és x=y=2. , valósokra ezzel meg is oldottuk a feladatot. Ha azt is feltesszük, hogy mindkettő egész, akkor is könnyű dolgunk van, ugyanis az 1 csak 1.1 és (-1).(-1) alakban bomlik két egész szám szorzatára, innen a megoldások: x=y=0 és x=y=2.
|
| Előzmény: [394] Korrob, 2008-03-25 17:26:39 |
|
| [394] Korrob | 2008-03-25 17:26:39 |
 Szervusztok! Nem vagyok valami jó matekból Elsőfokú diofantoszi egyenletekre kéne általános megoldás. ilyenekre pl.: xy=x+y 3x+7y=19 102x+45y=53 stb.
Előre is köszi.
|
|
|
| [392] Róbert Gida | 2008-03-24 11:55:23 |
 [Számlálóban a legkülső zárójel persze felesleges]
n egész, d osztója, akkor d társosztója n/d, azaz d és e osztó-társosztó, ha d*e=n teljesül, ekkor persze e társosztója d, így az osztók párokba rendezhetőek (előfordulhat, hogy önmaga lesz a társosztó, ha n négyzetszám. Például n=36 osztó-társosztó listája:
(1,36),(2,18),(3,12),(4,9),(6,6)
Ha ezt egy négyzetszámra végzed el: k2=d*e, akkor minden párban pontosan az egyik lesz legfeljebb k, kivéve, ha k=d=e, ez triviális, így a k-nál nem nagyobb osztók száma=k2 osztópárjainak a száma= , ha , ha 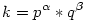 , akkor ebben az esetben ez , akkor ebben az esetben ez 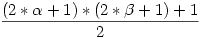
|
| Előzmény: [391] epsilon, 2008-03-24 11:42:42 |
|
| [391] epsilon | 2008-03-24 11:42:42 |
 Köszi Róbert Gida! Profi munka, és mégis elemi. A társosztóról röviden a lényeget hol olvashatom el pl. a neten, vagy elmondod-e egy pár szóban, mert a következő képlet nem jön be :-( Üdv: epsilon
|
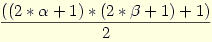 |
| Előzmény: [390] Róbert Gida, 2008-03-24 11:30:35 |
|
|
|
|
|





 0) a hibája), és nézzük meg, hogy x-re alkalmazva az iterációt, mekkora lesz a következő tag, azaz
0) a hibája), és nézzük meg, hogy x-re alkalmazva az iterációt, mekkora lesz a következő tag, azaz  d2k, és ilyenkor indítsuk az algoritmust dk-ból, ezzel az első jó pár lépést megspóroljuk.
d2k, és ilyenkor indítsuk az algoritmust dk-ból, ezzel az első jó pár lépést megspóroljuk. 


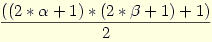
 +1)*(2*
+1)*(2* +1) pozitiv osztója van. Osztó társosztó fogalmát használva ezek közül
+1) pozitiv osztója van. Osztó társosztó fogalmát használva ezek közül 