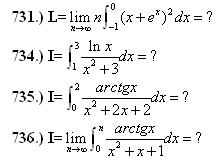| [510] Káli gúla | 2008-05-18 19:33:14 |
 Az egyenletet felírhatod abból kiindulva is, hogy a belső szögfelező egyenesének normálvektora a külső szögfelező iránya, ez pedig az oldalirányú egységvektorok különbsége: ÿ 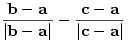 (|v| a vektor hosszát jelenti). Tehát a keresett egyenlet: (|v| a vektor hosszát jelenti). Tehát a keresett egyenlet:
|
| Előzmény: [507] komalboy, 2008-05-18 11:45:52 |
|
|
|
| [507] komalboy | 2008-05-18 11:45:52 |
 Sziasztok!
Valaki leírná általánosan a háromszög egyik belső szögének szögfelező egyenesének egyenletét??? előre is köszönöm
|
|
| [506] epsilon | 2008-05-02 20:12:36 |
 Helló Róbert Gida! A 659)-es feladatra ennél szebb, egyszerűbb megoldást elképzelni sem lehet, gatulálok, köszi! a 691)-es feladat esetén valóban úgy tűzték ki, hogy a limeszét kérték, de Én blöffnek láttam, minekutána az [503]-nál vázoltam a gondolatmenetet, hát azt nagyon át kell néznem, hogy miért hibás az, hogy egyenként kijön az a 6 integrálnak a közös pi/12 érték, de lehet, hogy nem hibás, hanem a limesszel már másként alakul. Szóval jó sejtésed volt, hogy a limeszt odatetted. Szóval most azt a megoldást is alaposa átmazyolázom, haddlám mit tévesztettem szem elől, a társintegráljaim esetén. Mindenképpen, ez a megoldásod lényegesen rövidebb mint amibe Én belekezdtem. Gratulálok, és kösz, üdv: epsilon
|
|
|
| [504] Róbert Gida | 2008-05-02 16:50:47 |
 De persze csak n tart végtelen esetén lesz annyi az integrál, adott n-re nem annyi. Számlálóval beosztva szebb az integrál:
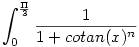
Ami így írva már kellemes, hiszen 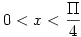 esetén 1<cotan(x), míg esetén 1<cotan(x), míg 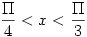 esetén 0<cotan(x)<1. Rögzített esetén 0<cotan(x)<1. Rögzített  >0-ra, amit integrálni kell az tart 1-hez a >0-ra, amit integrálni kell az tart 1-hez a ![[\frac {\Pi}{4}+\epsilon,\frac {\Pi}{3}]](keplet.cgi?k=D593301CFAF47485) intervallumon, így az integrál intervallumon, így az integrál 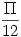 -höz tart. Míg -höz tart. Míg ![[\epsilon,\frac {\Pi}{4}-\epsilon]](keplet.cgi?k=4F33B6E6E51CB10C) intervallumon 0-hoz tart, így az integrál is. A kimaradó két intervallum hossza 0-hoz tart, de rajta korlátos függvényt integrálunk, így az integrál is 0-hoz tart, ha intervallumon 0-hoz tart, így az integrál is. A kimaradó két intervallum hossza 0-hoz tart, de rajta korlátos függvényt integrálunk, így az integrál is 0-hoz tart, ha  tart 0-hoz. Így az integrál tart 0-hoz. Így az integrál 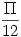 . .
|
| Előzmény: [503] epsilon, 2008-05-02 15:29:53 |
|
| [503] epsilon | 2008-05-02 15:29:53 |
 Helló! A feltételezhetően utolsó (?) integrál az alábbi: ezzel az a gond, hogy nagyon hosszas, és az eredmény duplája az-az pi/6 jött ki a pi/12 helyett. A megoldásvázlat: Legyen I ugyanaz az integrál mint a képen, de 0 és pi/2 között. Ezt felbontottam I=I1+I2+I3 integrálokra, pi/6 és pi/3 osztópontoknál. Hozzárendeltem a J=J1+J2+J3 társintegrálokat, amik ugyanolyanok mint az előzőek, de a számlálókban sin helyett cos van. Nem nehéz igazolni, hogy I=J=pi/4. Ezután változócseréket végeztem és I1=J3, és ilyesmik adódtak. Az lett a vége, hogy mind a 6 számozott integrál egyenlő, és közös értékük pi/12. De ezzel, a kitűzött feladat integrálja I1+I2=pi/6 és nem pi/12 :-( A megoldásom hibás, vagy a kitűzött feladatban a felső korlát pi/6 kellene legyen a pi/3 helyett? Vagy ??? Ez a feladat, kösz, üdv: epsilon.
|
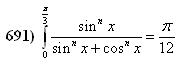 |
|
| [502] epsilon | 2008-05-02 15:11:49 |
 Helló! Szerencsémre már fogytá vannak az integrálok :-) Az alábbi integrállal csupán annyi a bajom, hogy Én az x/(3-x)= t×t változócserét láttam ésszerűnek, azzal kijön az adott eremény. Van valami egyszerűbb megoldás, ahol nem kell ennyit számolni? Előre is kösz, üdv: epsilon
|
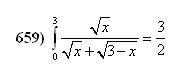 |
|
| [501] epsilon | 2008-05-02 09:07:35 |
 Kedves Káli gúla! Az általánostott ötleted alapján úgy látom, hogy a feladatom esetén elegendő olyan a, b valós számokat találni, amelyekre 2x+a<=f(x)<=2x+b. Ennek érdekében tekintetem egy g(x)=f(x)-2x-k segédfüggvényt a (-1;0) intervallumon. Mivel itt, ennek a deriváltja nem pozitív, ezért itt a g(x) monoton csökkenő, vagyis g(0)<=g(x)<=g(-1) ahonnan a=-k é b=1+1/e -k megfelel (sőt pl. k=1 esetén még egyszerűbbek a korlátok). Ezzl a közrefogássak, az általad leírt lineáris függvény integrálása alapján a limesz láthatóbban 1/2 (persze nem olyan szép általánosan mint Te írtad). És az f'(0) pedig az e(expx) Taylor sorbafejtés (a 0 körül) második tagjára emlékeztet. Most csupán az a "gondom", hogy mivel ez a feladat középisklásoknak feleletválasztós teszt, hogyan lehet ép ésszel meggyőzni egy jobbacska diákot, hogy miért éppen a 2x+k típusú fogófüggvényt kerestem, vagyis miért van ott 2 és miért nem MÁS szám? Én erre csak az e(expx) Taylor sorbafejtésévől látom az f(x)-ben 2 megjelenését...valami más emészthetőbb tipp? Ismételten köszönöm a tartalmas, szinvonalas segítségedet, ami nélkül nem lett volna ez a happy End. Üdv: epsilon
|
|
| [500] epsilon | 2008-05-02 08:33:38 |
 Kedves Káli gúla! Köszi, hogy foglalkozol a problémával, és általánosítottabb formában elsőfokú föggvénnyel próbáltad asszimptótikusan megközelíteni az integrandusz alatti függvényt. Megpróbáltam emésztgetni a leírtakat, de amikor az utolsó integrálhoz értem, vagyis amit lennebb beteszek, ahoz, hogy ott a limesz 1/2 legyen szükséges a k1=k2=2...és akkor az azelőtt levő x+e(expx) közrefogása egy egyenlőségé alakúlnak, ami nem igaz. Ha tévedek,vagy rosszul értettem valamit, légyszíves javíts ki, mert a feladat megoldása ami érdekel, nem az, hogy keressem a kákán a csomót...de úgy látom, hogy..ahol jeleztem, elakadtam. Előre is kösz, üdv: epsilon
|
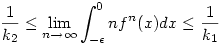 |
| Előzmény: [499] Káli gúla, 2008-05-01 23:13:41 |
|
|
| [498] epsilon | 2008-04-30 08:24:11 |
 Nagyszerű nadorp! Ez volt az egyetlen transzformáció ami változatlanul hagyta a nevezőt és a számlálóval is volt mit kezdeni. Természetesen a mezei integrál 4/4-el szorozva, azonnal kijön. Köszi szépen, ez sem volt piskóta, még maradt a 731. amire kiváncsi vagyok, megint egyedi-e a megoldása. A felygyült integráltesókat szerencsére ritkítottam, de ezek keményebb diók voltak Üdv: epsilon
|
| Előzmény: [497] nadorp, 2008-04-29 21:06:23 |
|
|
|
| [495] epsilon | 2008-04-29 13:57:56 |
 Ha segítene valamit, a 731.-nek a limesz értéke 1/2, próbáltam még Taylor sorral, az sem jött össze, a Newton Binomiális képlet az nem dobja ki az 1/2-öt, tehát ha azzal próbálom, valami összeg limeszeként kellene előálljon, de még mindig a rekurzióval próbálkozom, akár másodrendű is jó lenne...A 736-ot is a 735 mintájáta analóg változcserével, nem alakult úgy egyenlenek, mint a 735, a nevező megváltozott :-(
|
|
| [494] Sirpi | 2008-04-29 10:03:01 |
 Na ezt gondold át még egyszer :-) A függvény primitív függvénye valóban csak konstans erejéig meghatározott (legyen F(x)+c), de mivel rögzített intervallumon integrálunk, ezért az integrál értéke pl. az első esetben F(0)+c-F(-1)-c=F(0)-F(-1) teljesen független a konstans megválasztásától - ami nem is csoda, mert az integrál megegyezik ezen az intervallumon a görbe alatti területtel.
|
| Előzmény: [493] Róbert Gida, 2008-04-29 08:57:50 |
|
| [493] Róbert Gida | 2008-04-29 08:57:50 |
 Az első és az utolsó limesz persze csak úgy értelmes, hogy az integráloknál az integrációs konstans mindig 0, különben a limesz nem létezik, hiszen csak konstans erejéig meghatározott az integrál.
|
| Előzmény: [492] epsilon, 2008-04-29 06:44:10 |
|
| [492] epsilon | 2008-04-29 06:44:10 |
 A 731.-hez ha Valaki egy rekurziós öszefüggést tudna megállapítani, az is elég lene...
|
|
| [491] epsilon | 2008-04-28 16:18:35 |
 A 735. is hosszas ütközetek után kinyírva, az x=(2-t)/(1+2t) változócserével egy kiszámítható, meg az eredeti integrál ellentettje lett. Szóval ez sem volt piskót! Még maradt 2, de közben megint gyűlt vagy 10 :-(
|
|
| [490] epsilon | 2008-04-28 15:18:50 |
 Elnézést, a 731. feladatban a KÜLSŐ 2 helyett van az n (nem belül, ott e az x hatványon van), amásik esetben úgy van, ahogyan jonas kihangsúlyozta!
|
|
|
|
| [487] epsilon | 2008-04-28 09:50:50 |
 A 734. meglett :-) , szép feladat!
|
|
| [486] epsilon | 2008-04-27 10:37:40 |
 Helló!Megint gyűltek keményebb feladatok, a következő integrálok esetén sorra valahol belefulladtam, vagy regény lett a megoldásból :-( ha Valakinek van valami örlete, előre is köszönöm! Üdv: epsilon
|
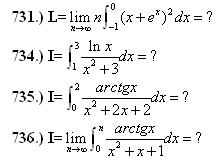 |
|






 ),b*sin(
),b*sin(
 >0-ra, amit integrálni kell az tart 1-hez a
>0-ra, amit integrálni kell az tart 1-hez a 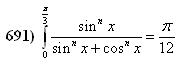
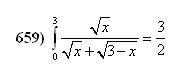
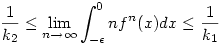
 0-val lehet felülről becsülni. Lineáris függvényekre könnyen kiszámolhatjuk az integrált -
0-val lehet felülről becsülni. Lineáris függvényekre könnyen kiszámolhatjuk az integrált - f(x)
f(x)

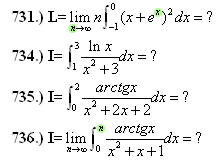

 , ráadásul az integrál se nehéz, hiszen csak az e2x-et, x.ex-et és x2-et kell hozzá integrálni, egyikkel sincs gond.
, ráadásul az integrál se nehéz, hiszen csak az e2x-et, x.ex-et és x2-et kell hozzá integrálni, egyikkel sincs gond.