|
| [560] Ágoston | 2008-07-13 21:05:12 |
 Tud valaki javasolni egy olyan ingyenes programot, amely segítségével matematikai ábrákat tudok szerkeszteni? Előre is köszönöm.
|
|
|
|
| [557] pocika75 | 2008-07-10 19:17:11 |
 Sziasztok! a segítségeteket szeretném kérni egy kis fejtörőhöz. van hozzá kedvetek?
|
|
| [556] jonas | 2008-07-10 13:02:35 |
 Ha erre szükséged van, akkor a nyilvános (akár külföldi) szerencsejáték sorsolásokon kívül használhatsz tőzsdei árfolyamokat, időjárási adatokat, vagy az olimpia alatt sporteredményeket.
|
| Előzmény: [555] jonas, 2008-07-10 12:59:56 |
|
| [555] jonas | 2008-07-10 12:59:56 |
 Szükséged van arra is, hogy a véletlen számaidat ne lehessen előre megjósolni (még részlegesen és nehéz számítással sem)? Ha nem, akkor használhatod valamilyen matematikai állandó (pl. 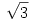 ) tizedesjegyeit, ahogy azt némely titkosítási szabvány teszi, vagy az Abramowitz-Stegun véletlenszám táblázatát, amely korlátozások nélkül elérhető és az interneten is meg lehet nézni. ) tizedesjegyeit, ahogy azt némely titkosítási szabvány teszi, vagy az Abramowitz-Stegun véletlenszám táblázatát, amely korlátozások nélkül elérhető és az interneten is meg lehet nézni.
|
| Előzmény: [549] Tibor, 2008-06-30 17:47:31 |
|
|
| [553] Róbert Gida | 2008-07-03 03:01:02 |
 Következő programot nézd meg (PARI-Gp-ben):
f(a)=c=10^100;N=random(c)+c;K=random(c)+c;\
while(1,N=nextprime(N+1);p=N;q=K+(a-N-K)%1001;if(isprime(q),print("n="p*q);print("p="p);print("q="q);return))
Ez egy ismert megvalósítása a problémának: p,q prímek n=p*q, úgy, hogy az elrejteni kívánt "a" számodra: (p+q) modulo 1001 = a teljesül. Nyilvánosságra hozod n értékét, majd amikor bizonyítani szeretnéd, hogy TE az "a" számra gondoltál 0-1000-ig, akkor nyilvánosságra hozod p és q értékét, az ellenőrzése a többiek számára, hogy nem csaltál:
1. n=p*q teljesül-e?
2. p és q prímek?
3. (p+q) == a mod 1001 teljesül-e?
Ezek mindegyike gyorsan ellenőrizhető akár a PARI-Gp-vel.
Persze ennél valamivel gondosabban kell megválasztani a prímeket, mert hiába lesz n>10^200, azaz nagyobb, mint a jelenlegi faktorizációs világrekord nem speciális számokra, vannak véletlen módszerek, amikkel n könnyedén faktorizálható: például akkor, ha p+1 vagy p-1 vagy q+1 vagy q-1 mindegyik prímfaktora "kicsi". Továbbá c értékét a programban célszerű módosítani, mert ugyanazon "a" értékekre futtatva ugyanazt az n-et adja a PARI indulásakor.
|
| Előzmény: [552] Tibor, 2008-07-02 20:06:38 |
|
| [552] Tibor | 2008-07-02 20:06:38 |
 Sajnos ahogy én akartam, arra nem alkalmas sem a kenó, sem a putto. Szóval az alapproblémám megmaradt. Kétnaponként kellene nekem 25 db háromjegyű véletlenszám. De úgy, hogy ellenőrízhető legyen: nyilvános, bárki által hozzáférhető számok valamilyen átformálásával kéne létrehozni. Van valakinek ötlete?
|
|
|
| [550] Róbert Gida | 2008-06-30 21:45:26 |
 Ha n számból húznak k számot és r számra tippelhetsz, akkor 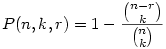 valószínűséggel lesz legalább egy találatod. Ahogy látod a komplemeter eseményt könnyebb kiszámolni, az pedig, hogy egy találatod sem lesz, a kedvező esetek és az összes esetek számát már könnyű számolni, a valószínűség pedig a kettő hányadosa lesz. valószínűséggel lesz legalább egy találatod. Ahogy látod a komplemeter eseményt könnyebb kiszámolni, az pedig, hogy egy találatod sem lesz, a kedvező esetek és az összes esetek számát már könnyű számolni, a valószínűség pedig a kettő hányadosa lesz.
Ez egyezik is az általad írtakkal: P(80,20,1)= , illetve P(80,20,61)=1 (persze, ha n-r<k, akkor , illetve P(80,20,61)=1 (persze, ha n-r<k, akkor 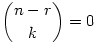 ). ).
|
| Előzmény: [549] Tibor, 2008-06-30 17:47:31 |
|
| [549] Tibor | 2008-06-30 17:47:31 |
 Sziasztok! Egy valószínűségszámítási problémám van. Egy játékhoz véletlenszámokat szeretnék előállítani, de úgy hogy ellenőrízhető legyen mások által is, hogy nem csalok. A kenóra gondoltam, mert azt minden nap húzzák. De nekem háromjegyű számok kellenének. Ráadásul különböző előzetes valószínűségekkel. Tehát a feladat: 80 számból húznak 20-at. Ha 1 számot tippelek, 25 százalék az esélye, hogy találatom lesz. Ha 61 számot tippelhetek, akkor 100 százalék az esélyem. De mennyi az esélye annak, hogy legalább egy találatom lesz, ha 2, 3, 4, ....stb számot tippelhetek? (Ez úgy lenne, hogy a nagyobb oddsokkal rendelkezők több számot tippelhetnek.) De ne gyertek azzal, hogy ez 10. osztályos tananyag, mert tudom. Sajna már régen tanultam. Valami ismétlés nélküli kombináció rémlik.... Köszi!
|
|
|
|
|
| [545] Ansible | 2008-06-23 23:41:29 |
 A Freud-Gyarmati: Szamelmelet-ben benne van, hogy az x2+5=y3-nek nincs megoldasa. Ez a 11.6.4/a feladat. A megoldas soran az  -ben alakitjuk szorzatta a baloldalt, es mivel ebben a gyuruben nem ervenyes a szamelmelet alaptetele, az idealokkal kell jatszani. -ben alakitjuk szorzatta a baloldalt, es mivel ebben a gyuruben nem ervenyes a szamelmelet alaptetele, az idealokkal kell jatszani.
Az x2+5=y3 ugyanebben a gyuruben alakithato szorzatta. Ketlem, hogy a fentinel kiralyibb ut lenne.
|
| Előzmény: [544] S.Ákos, 2008-06-23 21:32:04 |
|
| [544] S.Ákos | 2008-06-23 21:32:04 |
 Sziasztok! Valaki segítene megoldani az x2+20=y3 egyenletet, ha x,y N?. Előre is köszönöm. (x=14 y=6 jó, de y=2000-ig valószínűleg nincs más) N?. Előre is köszönöm. (x=14 y=6 jó, de y=2000-ig valószínűleg nincs más)
|
|
| [542] Csimby | 2008-06-08 17:41:37 |
 1.a: x -> 2x (x Z számhoz a kétszeresét rendeli, könnyen látható hogy ez injektív, szürjektív -> bijekció) Z számhoz a kétszeresét rendeli, könnyen látható hogy ez injektív, szürjektív -> bijekció)
1.b: x -> 2x+3
2.: Csak az a feladat, hogy valahogy felsoroljuk őket (ugye az hogy 0,1,2,3,... nem jó mert a negatívok kimaradnak): 0,1,-1,2,-2,3,-3,...
|
| Előzmény: [541] Norbert, 2008-06-08 17:20:09 |
|
| [541] Norbert | 2008-06-08 17:20:09 |
 Hi! Szerdán vizsgázok, sajnos és segítséget szeretnék kérni kettő feladatba mivel utálom a halmazokat. ELőre is köszönöm.
1. Adjon meg bijekciót két halmaz között: a) a pozitív egész számok halmaza és a páros pozitív számok halmaza; b) a [0,1] intervallum és a [3,5] intervallum.
2. Adja meg az egész számok halmazának egy sorozatbarendezését. (légyszi írja le vki hogy ez valójában mi vagy mit értünk ez alatt?)
|
|
| [540] Sirpi | 2008-06-02 07:44:04 |
 Az irracionális számok képe legyen önmaga; ekkor már csak a rac. számokat kell párosítani. Soroljuk fel az összes [0,1]-beli rac. számot (q1,q2,...), ezek közül az 1 legyen a qk. Ha i<k, akkor qi-hez rendeljük önmagát, ha i>k, akkor qi képe legyen qi-1 (így qk kivételével minden rac. számhoz hozzárendeltünk egy rac. számot).
* * *
Ugyanez kicsit egyszerűbben:
Ha az x [0,1) szám 1/2k alakú, akkor x [0,1) szám 1/2k alakú, akkor x 2x, ellenkező esetben x 2x, ellenkező esetben x x. x.
|
| Előzmény: [539] Gyöngyő, 2008-06-02 00:14:55 |
|
| [539] Gyöngyő | 2008-06-02 00:14:55 |
 Üdv! Aki tud légyszi segítsen megoldani a feladatot, mert szerdán sajnos vizsgázok. Előre is köszönöm.
Feladat: Adjon meg bijekciót a [0,1) és [0,1] halmazok között.
|
|
| [538] nadorp | 2008-05-23 07:54:54 |
 Tudom, hogy a példa már történelem :-), de itt egy közvetlen levezetés.
Legyen 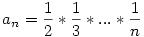
Ekkor 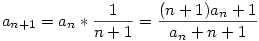 , így , így
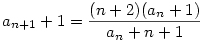 és és
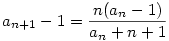 tehát tehát
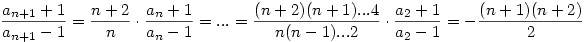
Innen 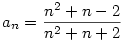 , ami persze azonos Sirpiével. , ami persze azonos Sirpiével.
|
|
|
|









 N?. Előre is köszönöm. (x=14 y=6 jó, de y=2000-ig valószínűleg nincs más)
N?. Előre is köszönöm. (x=14 y=6 jó, de y=2000-ig valószínűleg nincs más)
 2x, ellenkező esetben x
2x, ellenkező esetben x
 =1/c2. Akkor innen ismerhettem ezt a képletet.
=1/c2. Akkor innen ismerhettem ezt a képletet.