|
|
|
|
| [573] BohnerGéza | 2008-07-16 11:50:27 |
 Az általad megfogalmazott feladat pontosabban talán:
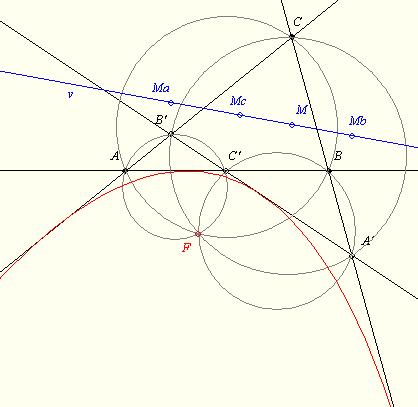
Ha négy egyenes négy háromszöget alkot, akkor ezek magasságpontjai egy egyenesen vannak, körülírt köreik egy ponton mennek át. ( Nem tudtam, de ez speciális esetben a Miquel-pont ) Ez a pont és a magasságpontok egyenese parabolát határoz meg, melynek az eredeti 4 egyenes érintője.
|
 |
| Előzmény: [570] zsolla, 2008-07-16 07:34:57 |
|
|
| [571] sakkmath | 2008-07-16 10:23:15 |
 Szerintem a Miquel-tételkört keresed (q  g). Keresd fel a Geometrikont itt. Klikkelj az M-betűre. A megjelenő, sorszámozott témakörök között a 410. a Miquel-pont, de érdemes megnézni a 407., 411. tételköröket is. g). Keresd fel a Geometrikont itt. Klikkelj az M-betűre. A megjelenő, sorszámozott témakörök között a 410. a Miquel-pont, de érdemes megnézni a 407., 411. tételköröket is.
|
| Előzmény: [570] zsolla, 2008-07-16 07:34:57 |
|
| [570] zsolla | 2008-07-16 07:34:57 |
 Valahogy igy lehetne, de szeretném pontosabban:
Ha a síkon felveszünk 4 egyenest, hogy azok 6 pontban metszék egymást, és 3 háromszöget alkossanak, majd megrajzoljuk a háromszögek köré írható köröket, akkor a körök egy pontban találkoznak, amit Miguel pontnak neveznek.
|
|
|
|
| [567] zsolla | 2008-07-15 20:29:01 |
 Pontosan meg tudná valaki határozni, hogy mit értünk Miguel ponton?
|
|
|
|
| [564] BohnerGéza | 2008-07-15 17:03:46 |
 A szerkesztőprogram lényege, hogy úgy kell vele szerkeszteni, mint körzővel és vonlzóval!
Nem helyettesíti a tudásod. Látványossabbá, pontossabbá, könnyebben elemezhetővé taszi a szerkesztést.
Azért néha könnyíti a dolgokat, pl. háromszög belső szögfelezőjéhez a beírt kör kp-ja egyből fölvehető.
|
| Előzmény: [562] Ágoston, 2008-07-14 21:22:10 |
|
| [563] Ágoston | 2008-07-15 11:23:20 |
 És címkéket hol lehet hozzáadni?
|
|
| [562] Ágoston | 2008-07-14 21:22:10 |
 Köszi szépen. Szögfelezőt hogyan lehet szerkeszteni?
|
|
|
| [560] Ágoston | 2008-07-13 21:05:12 |
 Tud valaki javasolni egy olyan ingyenes programot, amely segítségével matematikai ábrákat tudok szerkeszteni? Előre is köszönöm.
|
|
|
|
| [557] pocika75 | 2008-07-10 19:17:11 |
 Sziasztok! a segítségeteket szeretném kérni egy kis fejtörőhöz. van hozzá kedvetek?
|
|
| [556] jonas | 2008-07-10 13:02:35 |
 Ha erre szükséged van, akkor a nyilvános (akár külföldi) szerencsejáték sorsolásokon kívül használhatsz tőzsdei árfolyamokat, időjárási adatokat, vagy az olimpia alatt sporteredményeket.
|
| Előzmény: [555] jonas, 2008-07-10 12:59:56 |
|
| [555] jonas | 2008-07-10 12:59:56 |
 Szükséged van arra is, hogy a véletlen számaidat ne lehessen előre megjósolni (még részlegesen és nehéz számítással sem)? Ha nem, akkor használhatod valamilyen matematikai állandó (pl. 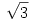 ) tizedesjegyeit, ahogy azt némely titkosítási szabvány teszi, vagy az Abramowitz-Stegun véletlenszám táblázatát, amely korlátozások nélkül elérhető és az interneten is meg lehet nézni. ) tizedesjegyeit, ahogy azt némely titkosítási szabvány teszi, vagy az Abramowitz-Stegun véletlenszám táblázatát, amely korlátozások nélkül elérhető és az interneten is meg lehet nézni.
|
| Előzmény: [549] Tibor, 2008-06-30 17:47:31 |
|
|
| [553] Róbert Gida | 2008-07-03 03:01:02 |
 Következő programot nézd meg (PARI-Gp-ben):
f(a)=c=10^100;N=random(c)+c;K=random(c)+c;\
while(1,N=nextprime(N+1);p=N;q=K+(a-N-K)%1001;if(isprime(q),print("n="p*q);print("p="p);print("q="q);return))
Ez egy ismert megvalósítása a problémának: p,q prímek n=p*q, úgy, hogy az elrejteni kívánt "a" számodra: (p+q) modulo 1001 = a teljesül. Nyilvánosságra hozod n értékét, majd amikor bizonyítani szeretnéd, hogy TE az "a" számra gondoltál 0-1000-ig, akkor nyilvánosságra hozod p és q értékét, az ellenőrzése a többiek számára, hogy nem csaltál:
1. n=p*q teljesül-e?
2. p és q prímek?
3. (p+q) == a mod 1001 teljesül-e?
Ezek mindegyike gyorsan ellenőrizhető akár a PARI-Gp-vel.
Persze ennél valamivel gondosabban kell megválasztani a prímeket, mert hiába lesz n>10^200, azaz nagyobb, mint a jelenlegi faktorizációs világrekord nem speciális számokra, vannak véletlen módszerek, amikkel n könnyedén faktorizálható: például akkor, ha p+1 vagy p-1 vagy q+1 vagy q-1 mindegyik prímfaktora "kicsi". Továbbá c értékét a programban célszerű módosítani, mert ugyanazon "a" értékekre futtatva ugyanazt az n-et adja a PARI indulásakor.
|
| Előzmény: [552] Tibor, 2008-07-02 20:06:38 |
|







 g). Keresd fel a Geometrikont
g). Keresd fel a Geometrikont 




