| [611] Doom | 2008-09-29 23:10:53 |
 Mert a jég térfogata nagyobb, mint az azonos tömegű vízé (azaz sűrűsége kisebb), így mikor megfagy, kitágul. Mivel a kupak általában jól rá van csavarva, így nem enged, ezért az üveg reped szét, hogy helyet adjon a jégnek.
|
| Előzmény: [610] Dorottya, 2008-09-29 19:15:49 |
|
| [610] Dorottya | 2008-09-29 19:15:49 |
 Valaki segítsen nekem! A vizesüveg miért reped szét hogyha lefagyasztom??? Sürgős lenne!!! Előre is köszike a segítségeteket!!!!!!
|
|
| [609] jenei.attila | 2008-09-29 13:24:48 |
 Természetesen ilyen 12-es futamot nem választ, sőt olyat sem, hogy akár csak egy hatos is szerepelt volna már eddig kiválasztott futamban. Ezt az biztosítja, hogy a kiválasztandó 12-es (vagy kisebb) futamot az összes eddig kiválasztottal összevetjük, és csak akkor fogadjuk el, ha mindegyikkel legfeljebb 5 közös eleme van. Ha bármelyik már kiválasztottal legalább 6 közös eleme van, akkor folytatjuk a keresést, méghozzá a csökkenő sorrendű súlyú versenyzőkön lexikografikusan tovább haladva (vagyis a nem megfelelő futam legkisebb súlyú versenyzője helyett a következő kisebb súlyút véve, sít.). Ilyen módod minden hatos kiválasztás csak egy 12-es futamban szerepelhet. A program pedig akkor áll le, ha az összes súly 0 (0 súlyú elemet soha nem választunk ki). Ez egyben azt is jelenti, hogy minden hatos kiválasztás szerepel valamelyik 12-es (vagy kisebb) futamban, hiszen egy versenyző súlya jelenti azt, hogy hány, még futamba nem sorolt hatosban szerepel. A súlyok minden futam kiválasztáskor csökkennek, méghozzá lehetőleg a nagy súlyok. Vagyis előbb-utóbb minden versenyző súlya 0 lesz.
|
| Előzmény: [608] jonas, 2008-09-29 12:24:32 |
|
|
| [607] jenei.attila | 2008-09-28 20:11:57 |
 Végülis van egy nem használt gépem, de a programom még ránézésre is elég ronda, minimális erőfeszítéssel csiszolható. Egyébként az algoritmus rendkívül egyszerű: felveszek egy 45 elemű tömböt, amely tartalmazza, hogy az adott indexű elem még hány olyan 6-os kombinációban szerepel, amiket a már kiválasztott 12-es (vagy kevesebb elemet tartalmazó) osztályok nem generálnak (legyen ez az adott elem súlya; kezdetben az összes elem súlya 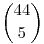 ). Pl. a tömb 1. eleme jelzi, hogy az 1-es szám még hány osztályozatlan 6-os kombinációban szerepel (ez az 1 súlya). Ezután az elemek csökkenő súlyának sorrendjében (tehát elsősorban nehéz elemeket választva) lexikografikusan generálom a 12-es kombinációkat egészen addig, amíg a kiválasztott 12-es (vagy kisebb) osztály a már kiválasztottak mindegyikével legfeljebb 5 közös elemet tartalmaz (ez biztosítja, hogy egy 6-os kombinációt csak egy osztály generál). Ha a megfelelő osztály kiválasztatott, akkor az említett tömbben a kiválasztott elemek súlyát annyival csökkentjük, ahány új 6-os kombinációban szerepel az illető elem. Az egész eljárást addig folytatjuk, amíg a súlyok mind 0-ák nem lesznek. A súly tömböt egyébként minden sikeres kiválasztás után csökkenőleg rendezem. ). Pl. a tömb 1. eleme jelzi, hogy az 1-es szám még hány osztályozatlan 6-os kombinációban szerepel (ez az 1 súlya). Ezután az elemek csökkenő súlyának sorrendjében (tehát elsősorban nehéz elemeket választva) lexikografikusan generálom a 12-es kombinációkat egészen addig, amíg a kiválasztott 12-es (vagy kisebb) osztály a már kiválasztottak mindegyikével legfeljebb 5 közös elemet tartalmaz (ez biztosítja, hogy egy 6-os kombinációt csak egy osztály generál). Ha a megfelelő osztály kiválasztatott, akkor az említett tömbben a kiválasztott elemek súlyát annyival csökkentjük, ahány új 6-os kombinációban szerepel az illető elem. Az egész eljárást addig folytatjuk, amíg a súlyok mind 0-ák nem lesznek. A súly tömböt egyébként minden sikeres kiválasztás után csökkenőleg rendezem.
|
| Előzmény: [606] jonas, 2008-09-28 18:44:16 |
|
|
|
|
|
| [602] Gyöngyő | 2008-09-28 13:55:06 |
 Sziasztok!
Kaptam egyenlőtlenségek cimű órán efy faladatot,de nem nagyon tudom rendesen bebizonyítani a feladatot. Tudnátok segíteni:
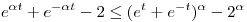 ahol t valós és alpha nagyobb vagy egyenlő mint 2 ahol t valós és alpha nagyobb vagy egyenlő mint 2
Üdv.: Zsolt
|
|
| [601] jenei.attila | 2008-09-28 11:31:47 |
 Nyilván a költségek miatt. Az általad adott kb. 50 ezer 12-es osztály 924*50000 hatos kombinációt generál, ami jóval több mint 45 alatt a 6. Így már bőven nem érné meg.
|
| Előzmény: [600] jonas, 2008-09-28 11:24:48 |
|
| [600] jonas | 2008-09-28 11:24:48 |
 Ebben az esetben miért fontos, hogy egy hatos kombinációt csak egyszer játszd meg? Nem éppen csak az fontos, hogy minden kombináció legalább egyszer szerepeljen, vagyis éppen az a könnyebb feltétel, amivel én adtam megoldást?
|
| Előzmény: [599] jenei.attila, 2008-09-28 11:13:06 |
|
| [599] jenei.attila | 2008-09-28 11:13:06 |
 Sajnos a project már nem aktuális, mert a 6-os lottó főnyereményt elvitték. A hatos lottóban kombinációs játék esetén maximum 12 szám jelölhető meg, amiből az összes kombinációt megjátsszuk. A cél az volt, hogy a lehető legkevesebb kombinációs játékkal az összes hatos kombinációt előállítsuk. Technikailag egyáltalán nem lett volna lehetetlen ilyen módon beküldeni az összes lehetséges hatos lottó kombinációt (ellentétben a szokásos ellenvetésekkel), ugyanis csak azt a 10-20 ezer 12-es kombinációt kellett volna elküldeni, azt is interneten keresztül. Erre készítettem volna egy programot (miután a megfelelő 12-esek le lettek generálva), ami szerintem maximum pár óra alatt végzett volna a beküldéssel. Ha összejön, nyilván megérte volna, hiszen a főnyeremény jóval nagyobb volt mint a játék költsége. "Apró" technikai akadály persze a játékhoz szükséges 1,6 milliárd ft. előteremtése, de erre az interneten terveztem klubot szervezni, amelyben mindenki a befizetése arányában részesült volna a nyereményből. Alapvetően szerintem az egész bizalmi okok miatt bukhatott volna meg, hiszen az egészet központilag kellett volna menedzselni, és biztosítani, hogy a befizetők tényleg hozzájutnak a pénzükhöz.
Persze elméletileg és programozás technikailag továbbra is érdekes a feladat, de most egy kicsit félretettem. Az általam írt algoritmus nagyon lassú (kb. egy hét alatt végezne), de megpróbálom majd még optimalizálni. Előnye viszont, hogy egy hatos kombinációt csak egy 12-es kiválasztásból kapunk meg. Ha elkészülök, közzéteszem az eredményt.
|
| Előzmény: [598] jonas, 2008-09-26 21:58:50 |
|
|
| [597] BohnerGéza | 2008-09-21 21:28:53 |
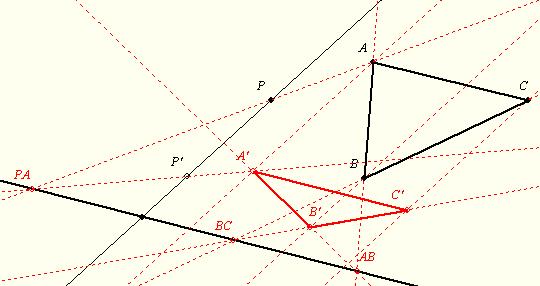
 Az ábrán adott a tengely (vastag fekete) P és a képe P' (ezek megadják az irányt és az arányt), valamint az ABC háromszög.
A szerkesztés - a tengelyen látható jelölések is segítenek - először P segítségével az A, majd A-val B és abból C. Természetesen más sorrend is jó, itt így fért az ábrára.
A szabályos ötszög szerkesztése így is lehetséges:
http://www.mindentudas.hu/laczkovichmiklos/20061103laczkovich1.html?pIdx=1
|
 |
| Előzmény: [596] Betty, 2008-09-21 10:15:08 |
|
| [596] Betty | 2008-09-21 10:15:08 |
 Könyörgök valaki segítsen!Egyszerűen most bejött másodikba egy új tantárgy,az ábrázoló geometria és NEM ÉRTEM.Ha valaki ért ehhez,az kérem mutassa meg milyen lesz egy szabályos 5szög tengelyes affinitásos képe,ha az affinitás tengelye nem azonos az 5szög egyik oldalával,hanem alatta van,és az affinitás iránya nem azonos az egyik oldal irányával...Előre is köszönöm!
|
|
| [595] jonas | 2008-09-20 20:14:57 |
 Ha az algoritmusod lassú, megpróbálhatod valamilyen szimmetriával felgyorsítani.
Arra gondolok, hogy veszel egy permutációcsoportot az n versenyzőn, és minden k-as futam mellé beveszed ennek a csoport összes elemével vett elmozgatását is. Legyegyszerűbb az n darab ciklikus eltolást venni, de lehet, hogy ennél nagyobbat is érdemes. Túl nagy csoportot ne vegyél, mert az már túlságosan megszoríthatja a megoldásodat. Arra persze vigyázni kell, hogy ugyanaz a m-es csoport ne szerepeljen többször egy kiválasztott futam pályájában. Speciálisan azt meg kell nézni előre, hogy minden csoporthoz legyen egy olyan futam, aminek a pályájában a csoport csak egyszer van benne. Még valami: ha segít, azt is megteheted, hogy a csoport n-nél néhánnyal több versenyzőn hat, és a nemlétező versenyzőket egyszerűen elhagyod a futamokból.
|
| Előzmény: [594] jenei.attila, 2008-09-20 12:35:13 |
|
| [594] jenei.attila | 2008-09-20 12:35:13 |
 Köszönöm a segítséget, de sajnos ezt még nem tudom használni. Az a baj, hogy egy hatos kombináció nagyon sok 12-esből előáll. Nekem az lenne jó, ha minden 6-os csak egyszer állna elő. Nem kell feltétlenül 12-es futamokat alkotni, lehet kevesebb versenyző is egy futamban. Az a cél, hogy lehetőleg kevés futam legyen. Írtam egy algoritmust, de sajnos nagyon lassú. További segítséget köszönettel veszek.
|
| Előzmény: [593] jonas, 2008-09-17 08:10:07 |
|
|
| [592] jonas | 2008-09-17 00:34:45 |
 A (43, 12, 6)-ra a kapott megoldásom tehát 38889 elemű, letölthető. Az n=43 versenyző az A,B,...,Z,a,b,...,p betűk jelölik. Minden sorban egy k=12 elemű mérkőzés van, ezek együtt lefednek minden m=6 elemű csoportot. (Az utolsó mérkőzésben van egy szóköz, ez azt jelenti, hogy az egyik pályán ezen a mérkőzésen senkinek nem kell indulnia.)
|
| Előzmény: [591] jonas, 2008-09-17 00:12:17 |
|
| [591] jonas | 2008-09-17 00:12:17 |
 Előállítottam egy megoldást (n=43, k=12, m=6) esetre, ez gyors gépen 73 perc alatt lefutott, és 38889 menetből állt, ami csak hatszor rosszabb, mint az egyszerűen kapott minimum, a 6598. A program teljesen egyszerű, nem használ semmilyen trükkös heurisztikát vagy visszalépést. Egyszerűen véletlen sorrendbe rakom az n alatt m csoportot, amiknek együtt kell játszania, mindig veszem ebben a sorrendben az első néhány olyan csoportot, aminek a tagjai még nem játszottak együtt, és az ezekben szereplő emberek játszanak. Lefuttatom ugyanezt a kicsit nagyobb n=45 esetre, és meglátjuk, mit kapok. Sajnos a kapott beosztás egy hozzászólásban nem fog elférni, úgyhogy kívülre rakom föl valahova.
|
| Előzmény: [589] jenei.attila, 2008-09-16 14:29:33 |
|
| [590] jonas | 2008-09-16 15:55:46 |
 Azt hiszem, erről valaki olyan algebristát kell megkérdezni, aki emlékszik valamire a csoportelméletből, vagy a szimmetrikus struktúrák vagy blokkrendszerek vagy hasonló nevű tárgyakból. Én szimmetrikus struktúrákat nem hallgattam, csoportelméletről pedig csak papírom van, de nem értek hozzá, ezért nem hiszem, hogy tudnék válaszolni. Lehet, hogy más valaki a fórumon tud segíteni; ha nem, akkor gondolom keresned kell valakit a fórumon kívül, aki ért ilyesmikhez.
|
| Előzmény: [585] jenei.attila, 2008-09-15 11:31:41 |
|
| [589] jenei.attila | 2008-09-16 14:29:33 |
 Ez így van. Nekem viszont m=6 bármely ponton át kéne lehetőleg egy egyens, amely legfeljebb k=12 pontot tartalmaz. Ez már nem affin sík lesz (mivel 6 ponton át általában nem húzható egyenes), de nem is annyira elméletileg, mint gyakorlatilag érdekelne a feladat. Legalább 8815 12-es beosztás kell, de egyáltalán nem biztos, hogy ennyiből megoldható. Ha ennek kb. kétszeresével megoldható, még az is jó.
|
| Előzmény: [588] Fálesz Mihály, 2008-09-16 14:19:44 |
|
|
|









