| [663] RRichi | 2008-11-06 22:42:44 |
 Az arcus cosinus (acos, arccos) függvény szolgál ennek megadására, számológépeken cos-1 -ként jelölik. Ha a működésére vagy kíváncsi, ajánlom a wikipédia ide vágó lapját, itt
|
| Előzmény: [661] szg, 2008-11-05 22:26:20 |
|
| [662] Gyöngyő | 2008-11-06 06:50:49 |
 Sziasztok!
Segitséget szeretnék kérni,hogy hogyan lehet Mapleval megoldani az alábbi feladatokat:B.3942,B3944,B.3948. Elöre is köszönöm!
Gyöngyő
|
|
| [661] szg | 2008-11-05 22:26:20 |
 Hali abban szeretném a segítségeteket kérni, hogy hogy tudom megkapni cos(x)-ből x-et? Vagy esetleg két egyenes által közbezárt szöget? Előre is köszönöm a választ vagy esetleg valami segítséget.
|
|
| [660] S.Ákos | 2008-11-05 20:56:50 |
 Sziasztok!
A következő angol mondat fordításában kérném a segítségeteket:
"Via the median-duality transforming an arbitrary triangle ABC into one formed by its medians..."
Előre is köszönöm,
Ákos
|
|
| [659] Kry | 2008-11-04 21:43:55 |
 igen középiskolás vagyok :)
a feladat cak az 1. egyenlet volt... a 2. at csak odaírtam hogy azt ne mondjátok mert odáig eljutottam
viszont közben rájöttem hogy csináljam meg ...
azért köszönöm segítettetek
|
|
| [658] rizsesz | 2008-11-04 21:05:59 |
 Középiskolás vagy :)?
A megoldás lényege egyszerűen annyi, hogy egy szám négyzete legalább 0, tehát ha kettőt összeadunk, akkor úgy lehet csak 0, ha mindkettő 0. Így jön ki a 43 és a -12. :)
A két egyenlet amúgy ekvivalens; ez azt jelenti, hogy ugyanazt mondják ki lényegében - azaz ha kifejted az alsóban a zárójeleket, akkor pont a felsőt kapod meg - tehát az egyik felesleges.
|
| Előzmény: [656] Kry, 2008-11-04 14:28:38 |
|
| [657] jonas | 2008-11-04 15:41:32 |
 A két egyenlet, amit felírtál, ekvivalens. Egy valós megoldása van, az x=43,y=-12, meg sok komplex megoldása, amiket együtt ennél egyszerűbben már nem lehet megadni.
|
| Előzmény: [656] Kry, 2008-11-04 14:28:38 |
|
| [656] Kry | 2008-11-04 14:28:38 |
 egy eggyenletben szeretnék segítségeteket kérni ... kimondottan a nevét sem tudom ennek a fajtának... és favágó módszerrel elég ronda számok jönnek ki
egy megoldóképletet vagy akár csak a nevét előre is köszönöm
|
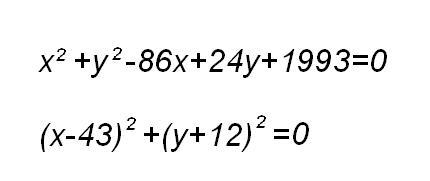 |
|
|
| [654] sakkmath | 2008-10-31 17:17:06 |
 A [602]-es és [631]-es hozzászólásokban látott feladat beküldési határideje a Monthly-ban lejárt. A feladatot sikerült megoldanom, s most közlöm e megoldást két, (remélhetően) egymást követő hozzászólásomban. Íme az I. rész:
|
 |
| Előzmény: [631] sakkmath, 2008-10-07 11:40:12 |
|
| [653] enyac | 2008-10-23 04:40:17 |
 Köszönöm szépen a segítséget, sikerült a zh-m! :-)
|
|
| [652] nadorp | 2008-10-20 14:18:55 |
 Természetesen alkalmazható, ezt nem is vitatom, (sőt még a végeredmény is meg fog egyezni :-), csak nekem mindig "hasogassa" a szememet :-) ha mezei deriválás helyett nagyágyút - L'Hospital-t használunk.
|
| Előzmény: [651] jenei.attila, 2008-10-20 11:46:56 |
|
|
| [650] nadorp | 2008-10-20 08:51:48 |
 Csak egy megjegyzés:
Ha g(x)=log2(x+2), akkor a feladat g'(0) értékét kérdezi, úgy hogy itt szerintem a L'Hospital szabály nem "való" ( ahogy a 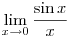 esetén sem), mivel a logaritmus deriváltjának meghatározásakor épp ezt a határértéket használjuk fel. esetén sem), mivel a logaritmus deriváltjának meghatározásakor épp ezt a határértéket használjuk fel.
|
| Előzmény: [646] enyac, 2008-10-19 19:08:01 |
|
|
|
| [647] S.Ákos | 2008-10-19 20:09:41 |
 Vizsgáljuk külön-külön a számláló és a nevező határértékét:
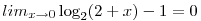
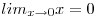
Mivel a határérték 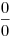 alakú, így az L'Hospital szabály alapján : alakú, így az L'Hospital szabály alapján :
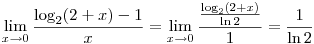
(remélem nem szúrtam el semmit)
|
| Előzmény: [646] enyac, 2008-10-19 19:08:01 |
|
| [646] enyac | 2008-10-19 19:08:01 |
 Köszönöm szépen a segítséget! Lenne még egy feladat, amiben nagyon sürgősen szükségem lenne segítségre (legkésőbb holnap reggelig) - nagyon szépen kérem, segítsetek, talán ezen múlik a zh-m...
Íme:
|
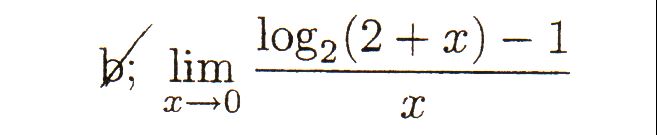 |
| Előzmény: [645] Lóczi Lajos, 2008-10-18 15:11:42 |
|
|
|
| [643] enyac | 2008-10-18 13:10:17 |
 Üdv!
Egy rövid kérdés: hol folytonos a sin x függvény egészrésze? Ahol nem folytonos, ott folytonossá tehető?
|
|
|
| [641] sanyikavagyok | 2008-10-12 21:39:11 |
 van egy házim amivel nem tudok mit kezdeni, mivel nem nagyon vagyok jó matekból, de azt is kell tanulnom:) segítenétek?
|
|
| [640] gmaccone | 2008-10-10 02:32:10 |
 Hello!
szerintem ha elkezded kibontani a rekúrziót akkor kapsz egy ilyet, hogy:
t(n)<=n+an+bn+t(a2n)+2t(abn)+t(b2n)<=...
(feltéve, hogy kommutatív számkörben operálunk:-)
végül:
t(n)<=n+n(a+b)+n(a+b)2+...+n(a+b)k+...
mértani sor összegképlet alapján LINEÁRIS BECSLÉST akkor tudsz adni, ha abszolút érték a+b<1 ugyanis akkor n/(1-(a+b))-vel tudod becsülni, de lehet, hogy én félreértettem a feladatot.
Peace
|
| Előzmény: [623] Algo, 2008-10-06 16:51:21 |
|
|







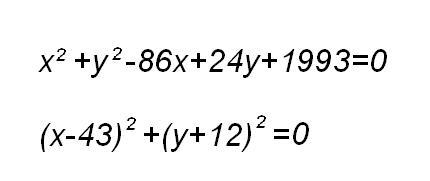

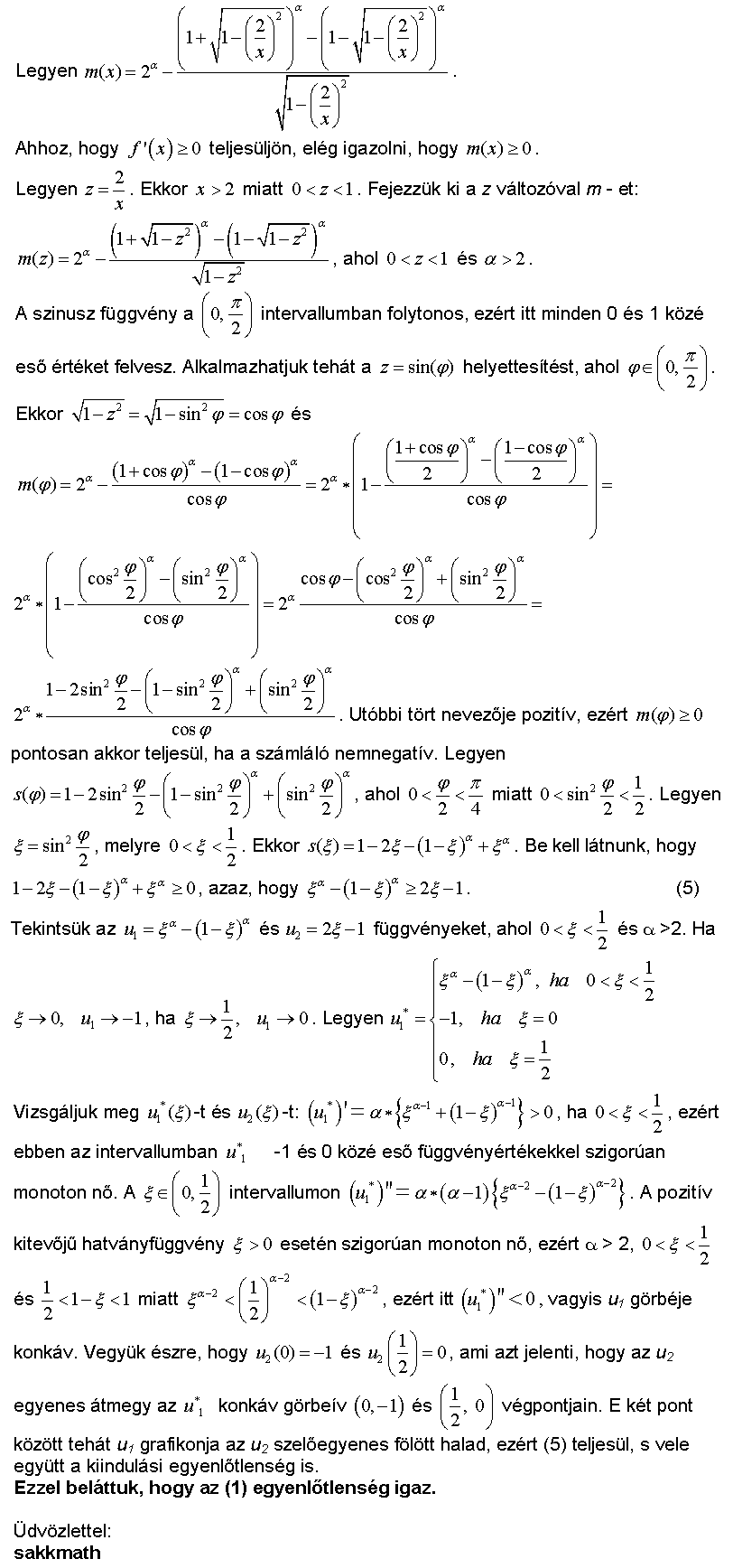


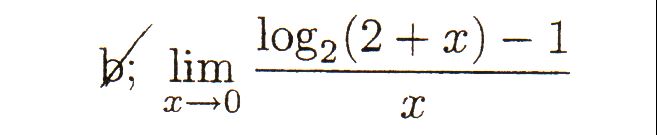

 /2-ben és ott folytonossá tehető.
/2-ben és ott folytonossá tehető.