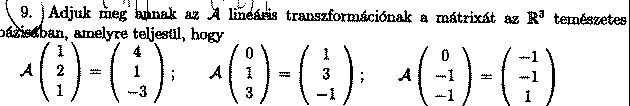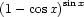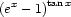|
|
| [697] szinuszhiperbolikusz | 2008-11-23 20:32:54 |
 Sziasztok!
Szerintem hagyjuk a jelszavamat, most van egy fontosabb problémám: (3x-2)/(x négyzet+4x+8) csúnyaságot kellene integrálnom ( bocsánat, de nem tok rendesen képletet szerkeszteni) Ti mit kezdenétek vele??? Köszi, SzH
|
|
| [696] j.milan | 2008-11-23 17:08:10 |
 Üdvözletem! Egy olyan technikai jellegű problémám merült fel, hogy elfelejtettem a jelszavamat. Nem találtam az oldalon sehol megfelelő emailcímet, akinél érdeklőhetek (lehet, hogy nem kerestem elég jól), ezért regisztráltam még egyszer, hogy itt kérdezzem meg. A régi accountomat azért szeretném használni többek közt, mert tesztversenyben is azt használom/tam... előre is köszönöm a segítséget
|
|
| [695] minoriole | 2008-11-23 16:52:29 |
 Mostmár napok óta agyalok ezen a problémán:
Nagyon sokmindent pubklikáltak már mátrixok sajátértékéről.
Ha van egy A mátrix akkor a karakterisztikus egyenlet megoldásával megkapjuk a sajátértéket és abból egyszerű egyenletekkel megkapjuk a sajátvektort.. de a másik irányról nem sokat hallottam:
Adott egy vektor, adjunk meg egy "sajátmátrixot" amire igaz hogy
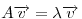
valamely  -ra. Több megoldás is létezik ?? És ha -ra. Több megoldás is létezik ?? És ha  =1 ? =1 ?
|
|
| [694] szinuszhiperbolikusz | 2008-11-21 19:43:56 |
 Sziasztok!
Először is köszönöm a választ, tetszik ez az oldal, valszeg még soxor fogtok engem itt látni!:) Annyit akarok kérdezni, hogy a jelszót nem lehet valahyogy változtatni? Én ugyanis olyat kaptam, hogy nemhogy megjegyezni, de még matematikai képlettel megoldani sem lehet! Köszi!
|
|
|
| [692] Sirpi | 2008-11-21 10:45:07 |
 A komplementer esemény kicsit egyszerűbb: az összes eset száma 40.30.20, hiszen az első húzás kizár 10, majd a második még 10 golyót, amiből választhatunk. A jó esetek száma pedig 36.27.18, hiszen először nem húzunk 10-est, ezt 36-féleképp tehetjük meg, ezután nem választhatjuk az első színt, se 10-est, vagyis marad 27 lehetőség, majd a 3. húzásnál 18. Tehát az eredeti kérdésre a válasz 1-(9/10)3. Érdemes észrevenni, hogy a megoldás nem függ a színek számától (feltéve, hogy van legalább 3).
|
| Előzmény: [690] C. Mars, 2008-11-20 16:50:20 |
|
| [691] Valezius | 2008-11-21 01:20:47 |
 Én így számolnám.
1. eset: elsőre tízest húzok, Másodikra és harmadik másik 2színt húzok. (4/40)*(30/39)*(20/38)
2. eset: elsőre nem tízest húzok, másodikra 10-est húzok, ami más színű, harmadikra egy harmadik színt húzok: (36/40)*(3/30)*(20/38)
3. eset első két alkalommal nem húzok 10-est, csak harmadikra, és persze mind különböző színű. (36/40)*(27/30)*(2/38)
Ezek összege adja a keresett valószínűséget.
|
| Előzmény: [690] C. Mars, 2008-11-20 16:50:20 |
|
| [690] C. Mars | 2008-11-20 16:50:20 |
 Üdv. Valaki legyen kedves, és árulja el az alábbi feladat megoldását. Előre is köszi!
Egy dobozban négyféle színű egyforma méretű golyók vannak, mindegyik fajtából 10 db, melyeket 1-től 10-ig megszámoztunk. Véletlenszerűen kihúztunk hármat. Mekkora az esélye, hogy köztük legalább az egyiken a 10-es szám szerepel, ha mind a három kihúzott golyó különböző színű?
|
|
| [689] Valezius | 2008-11-18 21:46:33 |
 Első lehetőség, a középiskolás módszer: felírsz 3egyenlet rendszert, és megoldod mindet.
Ha az eredeti mátrix 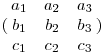
Akkor az első egyenletrendszer ugyebár: a1+2*a2+a3=4 a2+3*a3=1 -a2-a3=-3
A másik kettőben persze a bal oldal ugyanaz, csak bi és ci lesznek.
Egy másik lehetőség, hogy a 3egyenletrendszert együtt oldod meg elemi bázis transzformációval.
A megoldás:
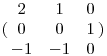
|
| Előzmény: [686] Alma, 2008-11-18 00:28:54 |
|
| [688] Alma | 2008-11-18 21:01:42 |
 Első megoldásvázlat ami eszembe jut:
Vedd úgy az egyenletek lineárkombinációját, hogy az A mátrix az (1,0,0), (0,1,0) és (0,0,1) vektorokra hasson. Ha ez megvan, akkor körülbelül csak le kell olvasnod a végeredményt: az i. egyenlet (az általam leírt sorrendben) jobb oldalán lévő vektor lesz a mátrix i. oszlopa, ahol i értéke 1, 2 vagy 3.
|
| Előzmény: [687] enyac, 2008-11-18 19:12:57 |
|
| [687] enyac | 2008-11-18 19:12:57 |
 Üdvözletem!
Az alábbi feladat megoldása kifogott rajtam, kérlek, segítsetek! Köszönöm szépen!
|
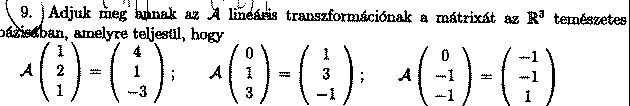 |
|
| [686] Alma | 2008-11-18 00:28:54 |
 Naaah ez nem volt szép :) A Taylor-sor tényleg hasznos dolog(bár inkább fizikások használják)
A fizika végig elhanyagolásokról szól tulajdonképpen, szóval nap mint nap kell ilyesmi közelítéseket használni, melyek igencsak megkönnyítik a számolást (az egy más kérdés, hogy matematikai tételek egzakt bizonyítására nem igen alkalmas). Hidd el, be lehet látni, hogy x->0 esetén igenis jogosak a közelítések. Vannak olyan esetek, amikor ezen közelítések nélkül meg sem tudnánk oldani egzaktul egy problémát.
Ilyen közelítést használunk például a matematikai inga lengésideje kiszámításakor (ott éppen a Sin(x)=x-et). Az általam leírt összefüggések természetesen csak x->0 esetén érvényesek (amit asszem sajnos elfelejtettem leírni :D), de akkor érdemes használni, ha csak számolni kell ezekkel.
off: van olyan órám is, ahol sqrt(2)=1,5 valamint Pi=3 és ehhez hasonlók. Bár hallottam rosszabbat is: állítólag az USAban valahol Pi=4gyel számolnak (nem tudom mennyire igaz). Ezekre többnyire azért van szükség, mert átláthatóbbá teszik a feladatot, és nem enged elveszni minket a részletekben.
Továbbá a fizika egyik módszere a dimenzióanalízis. Akkor alkalmazzák ezt a módszert, amikor elméletileg nagyon bonyolult jelenségeket vizsgálnak, és csak nagyságrendileg szeretnének megbecsülni valamit. A módszer lényege az, hogy végignézzük, milyen mennyiségektől függhet a keresett mennyiségünk, és megnézzük, ezek milyen kombinációjával kaphatunk olyan mértékegységű mennyiséget, mint ami nekünk kell. Ilyen esetekben előfordulhat, hogy az eredmény akár 100szorosát vagy 100ad részét kapjuk, mégis ér valamit ez a módszer. (Ezt azért írtam, hogy megpróbáljalak meggyőzni, hogy néha megéri közelíteni)
|
| Előzmény: [685] Tibixe, 2008-11-17 23:56:01 |
|
|
|
|
| [682] Valezius | 2008-11-17 13:15:50 |
 Szerintem a két feladatnál ugyanazt a trükköt lehet alkalmazni, mint az xx határértékének kiszámításánál. Nevezetesen e alapra alakítjuk, majd a kitevőt felírjuk hányados alakban, amire már alkalmazható a L'Hopital szabály. 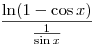
Deriválva a nevezőt és a számlálót:
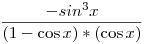 Illetve bővítve (1+cos x) -el Illetve bővítve (1+cos x) -el 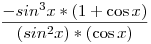 Amibe már be lehet helyettesíteni. Amibe már be lehet helyettesíteni.
Ugyanígy megkapható a másik is.
|
| Előzmény: [678] sandor720, 2008-11-16 20:57:51 |
|
| [681] Alma | 2008-11-17 00:58:13 |
 Én a helyedben első vagy másodrendig Taylor-sorba fejteném a kifejezéseket, és az alapján csinálnám meg (bár nem egzakt, de fél sorban kijön a végeredmény, ami mindenesetre nem hátrány :))(Wikipedia->Taylor series)
Ezeket a közelítéseket tenném meg:
Sin(x)=x
Tan(x)=x
Cos(x)=1-x*x/2
exp(x)=1+x/2
Ezek alapján szerintem mindkét határérték 1/2 (fejben csináltam, szóval egyáltalán nem biztos) Bocsi a csúnya írásmódért
|
| Előzmény: [677] sandor720, 2008-11-16 20:53:59 |
|
|
| [679] szinuszhiperbolikusz | 2008-11-16 22:54:25 |
 Valaki meg tudná mondani, mi az x az x-ediken deriváltja és le is vezetné??? Köszi!
|
|
|
| [677] sandor720 | 2008-11-16 20:53:59 |
 szia!
köszönöm a segítséget volna még kettő feladat. 1 feladat x 0+0
|
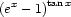 |
|
| [676] sandor720 | 2008-11-16 19:50:45 |
 Szia!
Euler gondolom erre gondoltál:2tgx/1/tg2x-re
|
|
| [675] Euler | 2008-11-16 18:10:42 |
 Gondolom a határérték a 0-ban kell, hiszen ott izgalmas a dolog.Használd a sinusra vonatkozó kétszeres szögfüggvényt, majd ezt ird be az első tag nevezőjébe, ezek után használd a kétszeres szög cosinusára vonatkozó összefüggést, ezt ird be a második tag nevezőjébe, hozz közös nevezőre, majd használd a trigonometrikus Pitagorasz tételt a számlálóban, a keresett határértk 1/2 lesz. Remélem érthető volt, amit leirtam és tudod használni.
|
| Előzmény: [674] sandor720, 2008-11-16 10:30:59 |
|



 -ra. Több megoldás is létezik ?? És ha
-ra. Több megoldás is létezik ?? És ha