| [769] jenei.attila | 2009-02-02 21:32:36 |
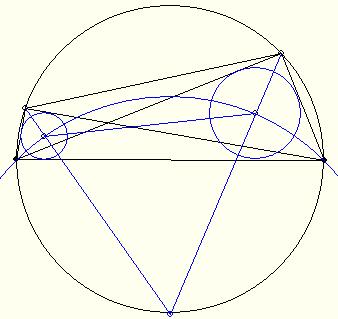
 Ha az adott pont 2 egységnél közelebb van a tengelyhez, akkor könnyű dolgod van. Egyszerűen ráilleszted a körlap szélét a tükrözendő P pontra úgy, hogy a körvonal két pontban metssze a tengelyt. Megjelölöd ezt a két pontot, majd a körlap szélét úgy illeszted ezekre, hogy most az előző helyzethez képest a tengelyre szimmetrikusan helyezkedjen el a körlap, majd körberajzolod a körlapot (a tengelyen kijelölt egymáshoz két egységnél közelebbi pontokra kétféleképpen-tengelyszimmetrikusan-illeszthető a körvonal). Ugyanezt megcsinálod mégegyszer úgy, hogy most az körvonal másik két pontban metssze a tengelyt. A körlap körberajzolásával adódó két körvonal metszéspontja a tengely másik oldalán megadja P tükörképét. Ha 2 egységnél távolabb van P a tengelytől, akkor segéd tengelyeket vehetsz fel úgy, hogy azok az eredeti tengely egy pontján menjenek át. A segédtengelyeket a fent leírt módon tükrözheted az eredeti tengelyre. Így az eredeti tengellyel együtt páratlan sok egy ponton átmenő tengelyed lesz, amelyekre sorban elvégezve a tükrözéseket (először a P-hez legközelebbi tengelyre türözve, majd továbbtükrözve a következő tengelyre, stb.) páratlan sok tükrözés után megkapod P tükörképét.
|
| Előzmény: [768] Ágoston, 2009-02-02 20:22:25 |
|
| [768] Ágoston | 2009-02-02 20:22:25 |
 Adott a síkon egy pont és egy egyenes. Körző használata nélkül szerkesszük meg a pontnak az egyenesre vonatkozó tükörképét. Használhatunk egyenes vonalzót a szokásos módon és egy egységsugarú körlapot, aminek nem ismerjük a középpontját. Ez utóbbit körvonalzóként használhatjuk, vagyis a síkon adott ponton, illetve pontokon átmenő egységsugarú körvonalakat tudunk rajzolni, de a középpontokat nem tudjuk bejelölni.
Valaki tudja a fenti feladatra a megoldást? Köszönöm
|
|
| [767] Tibixe | 2009-01-31 11:06:04 |
 Közben leesett, hogy amit tegnap írtam, az elég nagy hülyeség... Bocsássatok meg, elég álmos lehettem.
|
|
| [766] Tibixe | 2009-01-30 23:19:16 |
 Amit nekem sikerült, röviden:
Egy d=q-p behelyettesítés, utána a (p+d)p binomiális tételes kibontása, utána az egész szerencsétlenség leosztása pp+d-vel. Amit kapunk, az éppen a
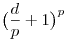
kibontott alakja lesz. Na ennek kéne 1-gyel egyenlőnek lennie. Tehát
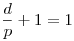
( esetleg -1, de az gyorsan kizárható ), innen pedig
d=0
.
|
|
|
| [764] Tibixe | 2009-01-30 20:14:52 |
 Úgy látszik eltér a humorérzékünk.
|
|
| [763] nadorp | 2009-01-30 19:24:28 |
 Köszi az építő megjegyzést, azért nem kell mindjárt leszedni az emberről a keresztvizet egy egyébként jó és nem bonyolult megoldás miatt ( lásd hentes) :-( Egyébként a számelmélet tele van analízist is tartalmazó bizonyítással,ezért nem értek Veled egyet teljesen. Én a pozitív egészeknek azt a tulajdonságát használtam, hogy számtani sorozatot alkotnak, Te meg a számelmélet alaptételét. Mindkettő jó. Ennyi.
|
| Előzmény: [761] Tibixe, 2009-01-30 16:26:18 |
|
| [762] Tibixe | 2009-01-30 16:36:04 |
 Hoppá,
sut tus tus
helyett
sut tus tus
-et akartam írni.
|
|
| [761] Tibixe | 2009-01-30 16:26:18 |
 Az analízissel szenvedjenek csak a fizikusok, az esetszétbontogatással meg a hentesek... Gyönyörűen kijön számelmélettel.
Vegyük mindkét oldal p alapú logaritmusát.
qp=(logp q) pq
Tehát logpq racionális, t/s alakban felírható, ahol t és s relatív prím egészek.
Innen
sqp=tpq
Ekkor lesz egy u pozitív egész szám, amire
p=ut q=us
Visszahelyettesítve:
t usut=s utus
Az általánosság megszorítása nélkül feltehetjük, hogy
sut ts ts
. Az előző egyenlet mindkét oldalát osztva:
t=s utus-sut
Az előző feltétel miatt utus-sut egész. Mivel t és s pozitív relatív prím egészek, utus-sut csak 1 lehet. Tehát t=s. Az egyetlen önmagával rel. prím pozitív egész pedig az 1. Innen pedig
p=u1=q
|
|
| [760] nadorp | 2009-01-30 08:09:03 |
 Ha p=1 akkor q=1 és fordítva, tehát ezekben az esetekben igaz az állítás. Feltehető, hogy p,q 2. Tegyük fel, hogy p<q. Ekkor a feladatban szereplő egyenlőség úgy állhat fenn, ha p kitevője nagyobb, azaz 2. Tegyük fel, hogy p<q. Ekkor a feladatban szereplő egyenlőség úgy állhat fenn, ha p kitevője nagyobb, azaz
qp>pq
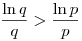
Mivel az 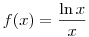 függvény x függvény x e esetén szigorúan monoton csökken, ezért 3 e esetén szigorúan monoton csökken, ezért 3 p<q esetén a fenti egyenlőtlenség nem állhat fenn. Marad a p=2 eset. Ekkor p<q esetén a fenti egyenlőtlenség nem állhat fenn. Marad a p=2 eset. Ekkor
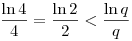 miatt szintén a monoton csökkenésből adódóan q<4,tehát csak q=3 lehet. Viszont a p=2 q=3 értékek esetén nem teljesül az eredeti egyenlőség. Azt kaptuk, p<q nem lehet. Teljesen hasonlóan adódik, hogy p>q sem lehetséges, tehát p=q miatt szintén a monoton csökkenésből adódóan q<4,tehát csak q=3 lehet. Viszont a p=2 q=3 értékek esetén nem teljesül az eredeti egyenlőség. Azt kaptuk, p<q nem lehet. Teljesen hasonlóan adódik, hogy p>q sem lehetséges, tehát p=q
|
| Előzmény: [759] Kiss Béla, 2009-01-29 20:53:36 |
|
| [759] Kiss Béla | 2009-01-29 20:53:36 |
 Sziasztok! Sagítséget szeretnék kérni a következő feladathoz. Foggalmam sincs, hogy hogyan lehetne megoldani:
Bizonyítsuk be, hogyha a p és q pozitív egész számokra fenn áll a pqp=qpq, akkor p=q.
|
|
|
| [756] Gyöngyő | 2009-01-24 10:26:40 |
 Sziasztok!
Lenne egy kérdésem!
Tudjuk,hogy 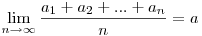
bizonyítsuk be,hogy
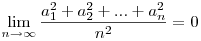
ahol ai pozitív valós számok.
Üdv.: Gyöngyő
|
|
| [755] HoA | 2009-01-22 18:47:09 |
 Ott viszont nem reagált rá senki. Idemásolom, hogy ne kelljen lapozgatni:
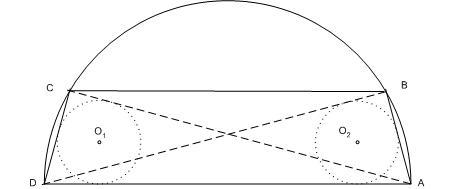
Az ABCD konvex négyszögben AD=2. Az ABD szög és az ACD szög derékszög. Az ABD háromszög szögfelezőinek metszéspontja gyök(2) távolságra van az ACD háromszög szögfelezőinek a metszéspontjától. Mekkora a BC oldal hossza?
Az ugye világos, hogy az adatok nem egyértelműen határozzák meg ABCD négyszöget. Kérdés, hogy BC hossza egyértelmű-e. Szimmetrikus esetben ABCD egyenlőszárú trapéz és elég könnyen kiszámolható, hogy ha 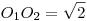 , akkor , akkor 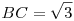
Feladatok:
- adjunk geometriai bizonyítást a szimmetrikus esetre
- adjunk bizonyítást az általános esetre
- igaz-e a tétel fordítottja: Ha 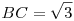 , akkor , akkor 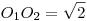 ? ?
|
 |
| Előzmény: [754] sakkmath, 2009-01-22 10:42:23 |
|
|
| [753] Valezius | 2009-01-21 20:22:43 |
 Láttam valamelyik topikban egy feladatot, de most az istenért se találom, valaki nem tudja, melyikben van?
ABCD konvex négyszög, ABD és ACD derékszög. Ugyanezekbe, mint háromszögbe írt körök középpontjai gyök(2) távolságra vannak.
Csak érdekelne, hogy jól emlékszem-e rá.
|
|
|
|
| [750] Gyöngyő | 2009-01-17 16:31:28 |
 Sziasztok!
Köszike Nadorp! Eszembe nem jutott,hogy sorbafejtesem.Nagyot koppant amikor elolvastam! Köszike még1szer!
|
|
|
| [748] nadorp | 2009-01-16 23:03:09 |
 Mivel nem volt logaritmus alap, ezért ez "hagyomány" szerint valóban ln-t jelent. Különben a 10-es alapú logaritmus lg. Az integrál kijön komplex integrállal is, ha az első negyedben levő egységnyi sugarú negyedkör ív és a két tengely által meghatározott zárt göbén integrálunk és a valós részeket nézzük, csak ez macerásabb számolás.
|
| Előzmény: [746] HoA, 2009-01-16 20:00:28 |
|
|
|
|
| [744] Gyöngyő | 2009-01-16 11:10:47 |
 Sziasztok!
Tud vki vmilyen ötletet adni a következő feladathoz: 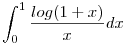
Thx: Gyöngyő
|
|





 tus
tus tus
tus