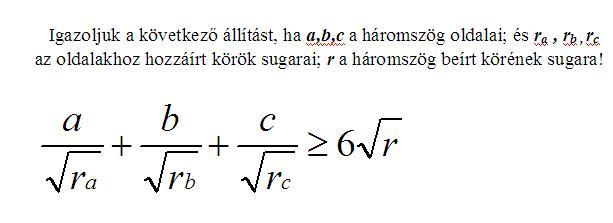| [801] sakkmath | 2009-02-16 10:19:18 |
 Ugyanez a kiinduló kör szerepel a következő feladatban is:
Adott az A(0; a) középpontú, a sugarú kör. A kör valamely - az origótól különböző - pontja legyen C. Tekintsük azokat a C-felezéspontú, OA-val párhuzamos szakaszokat, melyek hossza 2OC. Kérdések:
1. Mi a szakaszvégpontok mértani helye, ha C befutja a kört? 2. Mekkora területet zár be a mértani helyet leíró függvény görbéje? 3. Honnan lehet ismerős a kapott görbe? :)
|
| Előzmény: [795] HoA, 2009-02-15 07:45:55 |
|
|
| [799] nadorp | 2009-02-15 14:17:47 |
 2. megoldás
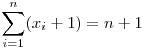 miatt a számtani és harmonikus közép közti egyenlőtlenségből miatt a számtani és harmonikus közép közti egyenlőtlenségből
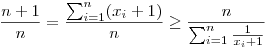 , tehát , tehát

Most felhasználva a mértani és harmonikus közép közti egyenlőtlenséget
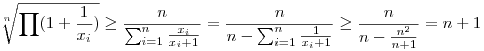
|
| Előzmény: [798] S.Ákos, 2009-02-15 13:56:02 |
|
| [798] S.Ákos | 2009-02-15 13:56:02 |
 Legyen a+b=2p és a-b=2q, ahol a,b,p,q pozitív valós számok. Vizsgáljuk az  kifejezést. a=p+q és b=p-q. Ezekkel a helyettesítésekkel: kifejezést. a=p+q és b=p-q. Ezekkel a helyettesítésekkel:
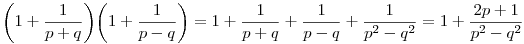
Ha 2p állandó, akkor ez a kifejezés szigorúan monoton nő a [0;p] intervallumon, ha tehát q csökken, akkor a kifejezés értéke is csökken. Ha a számok mind egyenlők, akkor 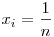 . Ha nem mind egyenlők, akkor van i,j úgy, hogy . Ha nem mind egyenlők, akkor van i,j úgy, hogy 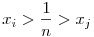 Legyen Legyen 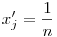 és és 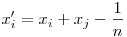 , és a többi xk-t hagyjuk változatlanul. Mivel xi+xj=xi'+xj' és xi>xj'>xj, ezért xi>xi'>xj, így xi-xj>|xj'-xi'|, így a kifejezés értéke csökkent, így a minimum csak x1=x2=...=xn esetén állhat, ami épp a jobb oldal. , és a többi xk-t hagyjuk változatlanul. Mivel xi+xj=xi'+xj' és xi>xj'>xj, ezért xi>xi'>xj, így xi-xj>|xj'-xi'|, így a kifejezés értéke csökkent, így a minimum csak x1=x2=...=xn esetén állhat, ami épp a jobb oldal.
Remélem érthető.
|
| Előzmény: [797] Gyöngyő, 2009-02-15 12:21:18 |
|
| [797] Gyöngyő | 2009-02-15 12:21:18 |
 Sziasztok!
Szeretnék segítséget kérni a következő feladathoz:
Legyenek xi>0,i=1,..,n
x1+x2+...+xn=1. Igazoljuk,hogy :
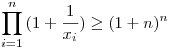
Üdv.: Gyöngyő
|
|
| [796] laci777 | 2009-02-15 11:20:46 |
 Kedves HoA!
Az első megoldásod egyszerű, és így nagyszerű:) A második viszont - a magam szinjéhez képest meg végképp -remekmű. Mindkettőt köszönöm!
|
| Előzmény: [795] HoA, 2009-02-15 07:45:55 |
|
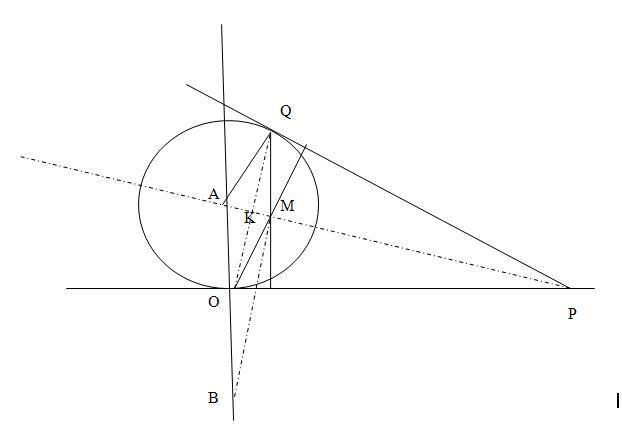
| [795] HoA | 2009-02-15 07:45:55 |
 Legyen a (0;a) pont A, a (0;-a) pont B, a PQO  magasságpontja M. AQ és OM párhuzamosak, mint PQ-ra merőleges egyenesek. AO és QM párhuzamosak, mint PO-ra merőleges egyenesek. Így OMQA paralellogramma és AO = AQ ( a kör sugara ) miatt rombusz. Átlói merőlegesek, középpontját K-val jelölve AKO magasságpontja M. AQ és OM párhuzamosak, mint PQ-ra merőleges egyenesek. AO és QM párhuzamosak, mint PO-ra merőleges egyenesek. Így OMQA paralellogramma és AO = AQ ( a kör sugara ) miatt rombusz. Átlói merőlegesek, középpontját K-val jelölve AKO  derékszögű. Ezt A-ból kétszeresére nagyítva K M-be O pedig B-be kerül. AMB derékszögű. Ezt A-ból kétszeresére nagyítva K M-be O pedig B-be kerül. AMB  derékszögű, tehát M valóban AB Thálesz-körén van. derékszögű, tehát M valóban AB Thálesz-körén van.
Mivel a feladatot koordináta-geometriai megfogalmazásban tűzték ki, oldjuk meg így is. Legyen P (p;0). Q az AP átmérőjű körön van, ennek középpontja (p/2;a/2), sugara 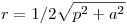 , egyenlete (x-p/2)2+(y-a/2)2=1/4(p2+a2) , (2x-p)2+(2y-a)2=p2+a2 ; 4x2-4xp+p2+4y2-4ya+a2=p2+a2 ; , egyenlete (x-p/2)2+(y-a/2)2=1/4(p2+a2) , (2x-p)2+(2y-a)2=p2+a2 ; 4x2-4xp+p2+4y2-4ya+a2=p2+a2 ;
4x2-4xp+4y2-4ya=0
Q az eredeti körön is rajta van, ennek egyenletét néggyel szorozva 4x2+4(y-a)2=4a2 ; 4x2+4y2-8ay+4a2=4a2 ;
4x2+4y2-8ay=0
A két egyenlet különbségéből a metszéspontokra y/x = p/a ( amit persze az ábráról mint OQ meredekségét könnyen leolvashatunk) , behelyettesítve 4x2+4p2x2/a2-8px=0 Egyik metszéspont az origó, erre nem vagyunk kíváncsiak, x-szel oszthatunk: x(4+4p2/a2)=8p ; x=2p/(1+p2/a2) Ez tehát Q és egyben M abszcisszája (Mx). M ordinátáját (My) abból számíthatjuk, hogy M rajta van az AP egyenesen: x/p+y/a=1 ; y=a-(a/p)x=a-2a/(1+p2/a2)=(a+p2/a-2a)/(1+p2/a2)=(p2/a-a)/(1+p2/a2) . Tekintsük az Mx2+My2 kifejezést:
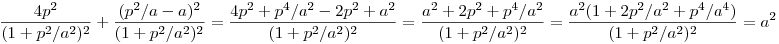 M tehát valóban az origó középpontú a sugarú körön, AB Thálesz körén van. M tehát valóban az origó középpontú a sugarú körön, AB Thálesz körén van.
|
 |
| Előzmény: [794] laci777, 2009-02-14 22:35:15 |
|
| [794] laci777 | 2009-02-14 22:35:15 |
 Megint geometria-példában kérnék szépen segítséget: vegyük az x2+(y-a)2=a2 egyenletű kört (az "a" tetszőleges, de rögzített értékű pozitív valós szám). E körhöz az x tengely egy tetszőleges P pontjából érintőt húzunk (nem az origóba). Ezt az érintési pontot Q-val jelölve,határozzuk meg a PQO(O az origo) háromszög magasságpontját. Ha végighaladunk x tengely valamennyi P pontján, mit adnak ki e háromszögek magasságpontjai? Az látszik, hogy a (0;a) és a (0;-a) pontok által meghatározott szakasz Thalész-köre a megoldás a két előbbi pont nélkül - de bizonyítani már nem tudom. Tudna valaki valamilyen kiinduló pontot, ötletet javasolni? Köszönöm előre is.
|
|
|
|
|
| [790] laci777 | 2009-02-13 22:31:43 |
 Ajjaj, már látom, s(c) és c metszésére tükrözzük C-t, így kapjuk a paralelogrammát. Késő van, egyébként is lassú vagyok:(
Még egyszer köszönöm, kellemes hétvégét.
|
|
| [789] laci777 | 2009-02-13 22:18:34 |
 Kedves Euler, köszönöm szépen, érthető voltál - azt hiszem, a 3szög súlyvonalára az oldalai függvényében adott képletre az életben nem jöttem volna magamtól rá (más kérdés, még most sem nagyon látom az s(c) és az m(c) c-n való távolságának számíthatóságát - de kicsit még emésztem). Még egyszer köszönöm.
|
| Előzmény: [788] Euler, 2009-02-13 18:17:09 |
|
| [788] Euler | 2009-02-13 18:17:09 |
 Paralelogrammára igaz az összefüggés, igy innen adódik, hogy egy háromszög súlyvonala kiszámolható a következő módon: 4sc2=2a2+2b2-c2(csúnya, de remélem érthető). Jelöljük a négyszög csúcsait rendre A, B, C, D-vel, AC felezőpontja E, BD felezőpontja F, ekkor4EF2=2CF2+2AF2-AC2, hasonlóan CF2 és AF2 kifejezhető a DBC és DAB háromszögekből, ezekat beirva az előbbibe már adódik is az állitás. Remélem érthetően sikerült leirnom.
|
| Előzmény: [786] laci777, 2009-02-13 15:21:23 |
|
|
| [786] laci777 | 2009-02-13 15:21:23 |
 Üdvözlet Mindenkinek!
Egy 11.-es versenyfeladat így szól: bizonyítsuk be, hogy tetszőleges konvex négyszög oldalai négyzetösszegéből annak átlói négyzetösszegét kivonva az átlók felezőit összekötő szakasz négyzetének négyszeresét kapjuk.
Megköszönnék bármilyen kiinduló pontot, gondolatot. Eddig még csak az oldal szakaszfelelők által meghatározott paralelogrammával próbálkoztam, de nem sok sikerrel (vagy nem elég kitartóan). Csak annyit tudok, hogy ez az állítás paralelogrammák esetén igaz.
Köszönöm előre is.
|
|
| [785] Sirpi | 2009-02-13 14:49:29 |
 Ismert, hogy T=s.r=(s-a).ra=(s-b).rb=(s-c).rc
Helyettesítsük be az r-eket a bizonyítandó egyenlőségbe:

Átszorozva 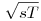 -vel és beírva a Heron-képletet ( -vel és beírva a Heron-képletet ( ), azt kapjuk, hogy ), azt kapjuk, hogy
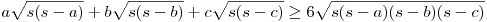
Legyen most x:=s-a, y:=s-b, z:=s-c. Ekkor a=y+z, b=x+z, c=y+z. T-vel leosztva, és ezeket beírva:
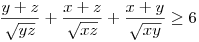
És ez igaz, mert minden tag legalább 2, hiszen minden x-re x+1/x 2, így az első tag is: 2, így az első tag is:
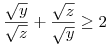
|
| Előzmény: [783] komalboy, 2009-02-13 10:16:19 |
|
| [784] matlány | 2009-02-13 10:34:23 |
 Sakkmath!
Tényleg vázlatos, amit Ön leírt. Esetleg le tudná írni bővebben, mert érdekel ennek a megoldása. Előre is köszönöm.
|
|
|
|
|
| [780] MTM | 2009-02-12 19:16:49 |
 Csak úgy...:]
A feladat: C. 593. Péter a bélyeggyűjteményéből az 1,2,3,...,37 forintos bélyegek mindegyikéből kivett egy-egy darabot. Szeretné ezeket úgy csoportosítani, hogy mindegyik csoportban ugyanannyi legyen a bélyegek névértékének összege. Hányféleképpen teheti ezt meg?
Minta a dolgozatok fejlécéhez C. 593. Nagy 163 Róbert 9. évf. Győr, Révai M. Gimn. e-mail: robi@revai.hu
Jelöljük a kapitány életkorát (években kifejezve) K-val, a hajóét H-val. A hajó H-K évvel ezelőtt volt annyi idős, mint a kapitány most; akkor a kapitány K-(H-K)=2K-H éves volt. Amikor a hajó 2K-H éves lesz, akkor a kapitány ...
|
| Előzmény: [779] rizsesz, 2009-02-12 19:02:06 |
|
|
| [778] vihand | 2009-02-12 18:53:17 |
 Helló, valaki meg tudja nekem röviden írni, hogy hogy kell kinéznie egy kísérőjegyzéknek? Sajnos elhagytam az első újságot, és eddig abból néztem ki. Nem sürgős, de örülnék neki. Előre is köszönöm a segítséget.
|
|
| [777] sakkmath | 2009-02-12 13:31:34 |
 Vázlatosan:
1) Az első egyenlet értelmezése.
2) Egy adott helyettesítéssel felírhatjuk a konvex függvényekre vonatkozó Jensen-egyenlőtlenséget.
3) A számtani - mértani közép összefüggésének kétszeri alkalmazása.
4) Az első pontban kapott eredménnyel kijön a megoldás.
|
| Előzmény: [776] komalboy, 2009-02-12 10:57:31 |
|








 magasságpontja M. AQ és OM párhuzamosak, mint PQ-ra merőleges egyenesek. AO és QM párhuzamosak, mint PO-ra merőleges egyenesek. Így OMQA paralellogramma és AO = AQ ( a kör sugara ) miatt rombusz. Átlói merőlegesek, középpontját K-val jelölve AKO
magasságpontja M. AQ és OM párhuzamosak, mint PQ-ra merőleges egyenesek. AO és QM párhuzamosak, mint PO-ra merőleges egyenesek. Így OMQA paralellogramma és AO = AQ ( a kör sugara ) miatt rombusz. Átlói merőlegesek, középpontját K-val jelölve AKO 





 2, így az első tag is:
2, így az első tag is: