| [856] Lóczi Lajos | 2009-03-08 20:00:58 |
 Ha a diszkrimináns kisebb nullánál, a képlet formálisan ugyanaz, csak konjugált komplex számokat tartalmaz (amelyek együttesen valós értéket adnak). De az Euler-összefüggésekkel ezt az esetet mindig átírhatod exponenciális függvényt és szinuszt/koszinuszt tartalmazó alakra, amiben már csak valós számok vannak.
|
| Előzmény: [854] akinom91, 2009-03-07 13:03:18 |
|
|
| [854] akinom91 | 2009-03-07 13:03:18 |
 Köszönöm szépen mind a két megoldási módot, sikerült az explicit képletet is megkapni (igaz, segítséggel, még életemben ilyet nem csináltam). A lényeg, hogy mind a 2 hasznos volt, tanultam valami újat, csak máskor is fel tudjam magamtól is használni. Ha már itt tartunk valaki fel tudná nekem írni, hogy a Fibonacci-féle sorozatot, hogy kell megadni explicit módon? Ezt kaptam:
Fibonacci sorozat: apn+1=bpn+cpn-1
Karakterisztikus egyenlet: aR2=bR+c; R1, R2 a karakterisztikus egyenlet megoldásai.
Ha R1=R2 => pn=R1n(A+nB); Ha R1 R2 => pn=R1nA+R2nB; (Ha valamit elírtam, javítsatok!) R2 => pn=R1nA+R2nB; (Ha valamit elírtam, javítsatok!)
Ott akadtam meg, ha a karakt. egyenlet esetében  <0. Ilyen esetben, hogy lehet felírni az explicit képletet? <0. Ilyen esetben, hogy lehet felírni az explicit képletet?
Előre is köszi!
|
| Előzmény: [853] Káli gúla, 2009-03-07 00:54:41 |
|
| [853] Káli gúla | 2009-03-07 00:54:41 |
 Ha E-vel jelölöd a csupa egyesekből álló mátrixot, akkor A=E-I, tehát A2+A=(E2-2E+I)+(E-I)=E2-E, ami a csupa kettesekből álló mátrix, ezért A2+A=2E=2(A+I). Ez ugyanaz, mint az a), és ebből A-val szorzással, indukcióval adódik a c) is.
|
| Előzmény: [852] akinom91, 2009-03-06 23:19:33 |
|
| [852] akinom91 | 2009-03-06 23:19:33 |
 Hát sajnos az első megoldásodnál fogalmam sincs, miről beszélsz, a másodikat meg nagyjából értem, amennyit leírtál (én is valami képletet próbáltam keresni). Meglátjuk, sikerül-e explicit képletet találni, ugyanis még ilyet nem oldottam, és nem tudom mennyire lehet gimnáziumi szinten... . És akkor a képletet amit feltételezzük, hogy megkapok, kell még bizonyítani mat. ind. módszerével, vagy ez már megvolt? :D Köszi a tippet az elinduláshoz, remélem érettségiig már kívülről fújom a típusfeladatok megoldásainak módszerét. :)
|
| Előzmény: [851] jonas, 2009-03-06 22:50:12 |
|
| [851] jonas | 2009-03-06 22:50:12 |
 A (c) pontot többféleképp is meg lehet közelíteni. Az egyik lehetőség, hogy az A mátrixot Jordan blokk alakra hozod, és ezt hatványozod.
A másik, hogy felhasználod az (a) pontot, amely szerint A2=A+2I ami alapján A3=A(A2)= A(A+2I)=A2+2A=3A+2I. Ebből megsejted, hogy az általános hatvány felírható An=pnA+qnI alakban. Valóban: An+1=A.An= A(pnA+qnI)=pnA2+qnA= (pn+qn)A+2pnI. Ebből pn+1=pn+qn, és qn=2pn, amiből pn+1=pn+2pn-1. A kezdeti feltétel is nyilván teljesül: p0=0,q0=1, p1=1,q1=0. (Persze ellenőrizned kell, hogy nem számoltam el.) Ennek a rekurziónak megkeresheted az explicit képletét. (Ez elvileg nem, csak gyakorlatban egyszerűbb annál, mintha az An mátrix mind a kilenc elemére írnál föl együttes lineáris rekurziót.)
|
| Előzmény: [850] akinom91, 2009-03-06 22:33:50 |
|
| [850] akinom91 | 2009-03-06 22:33:50 |
 Kérem, valaki segítsen megoldani a c.) pontot, esetleg az a.) pontot Cayley-Hamilton összefüggéssel (nekem csak egyszerű számítással sikerült). Előre is köszönöm!
|
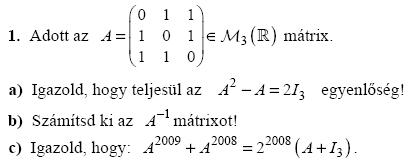 |
|
|
|
|
| [846] nadorp | 2009-03-02 10:51:34 |
 A pozitív definitséghez szerintem nem kell szimmetrikus mátrix. Egy valós nXn A mátrix pozitív definit, ha minden x=(x1,...,xn) vektorra xTAx>0. Az már egy másik dolog, hogy kvadratikus alakok definitségének vizsgálatához már szimmetrikus mátrixokkal dolgozunk, mert az egyszerűbb.
Van egy egy tétel is, mely szerint egy A mátrix pozitív definit akkor és csak akkor ha a  mátrix pozitív definit (http://mathworld.wolfram.com/PositiveDefiniteMatrix.html). Úgy hogy az az Obádovics példa nem biztos hogy hibás. mátrix pozitív definit (http://mathworld.wolfram.com/PositiveDefiniteMatrix.html). Úgy hogy az az Obádovics példa nem biztos hogy hibás.
|
| Előzmény: [845] pvong17, 2009-03-02 00:00:39 |
|
| [845] pvong17 | 2009-03-02 00:00:39 |
 Én kérek bocsánatot. Nem irtam le pontosan a feladatot és megzavart egy másik feladat. (Konkrétan Obádivics Gy. Lináris algebra -zöld könyv- 258.o 3.példája, ami ezek szerint hibás , mert egy nem szimm mátrixról(valós) állitja hogy poz defeinit, majd utána be is bizonyitja ezt :) )
Most már nincs probléma, mert sikerült letisztáznom a dolgokat. Köszönöm a gyors reakciót.
|
| Előzmény: [844] Lóczi Lajos, 2009-03-01 20:46:41 |
|
|
|
|
| [841] pvong17 | 2009-03-01 15:21:48 |
 Ha egy nem szimmetrikus mátrixnak, létezik negatív sajátértéke akkor már nem is lehet pozitív definit, ugye ?
(bocsánat ha triviális)
|
|
| [840] fityfiritty | 2009-02-26 17:01:02 |
 Nagyon jó!! Köszönöm Neked is és Jonasnak is a profi, klassz válaszokat, tanácsokat. Most már meg merem kockáztatni, hogy az ex hatványsorának az x = -1- hez tartozó részletösszegéhez jutottunk, ha nem tévedek. Ezért a limeszre a tippem: 1/e. Üdvözöl mindenkit: fityfiritty.
|
| Előzmény: [832] nadorp, 2009-02-25 15:50:24 |
|
| [839] sakkmath | 2009-02-26 12:20:11 |
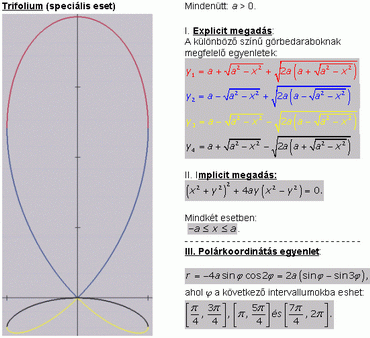
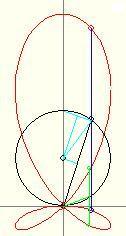
 Az egyes levelek területeire én is ezeket az eredményeket kaptam. Levezetésedben a teljes területre, mint adott értékre támaszkodsz. Hogy ez a szál se legyen elvarratlan, felteszem az alábbi ábrát, amely további adatokat szolgáltat a görbéről. Így bárki összevetheti saját eredményeit az általam közöltekkel... .
|
 |
| Előzmény: [833] HoA, 2009-02-25 16:40:55 |
|
|
|
|
|
|
| [833] HoA | 2009-02-25 16:40:55 |
 Ha a választott abszcisszához tartozó két másik metszéspontot is bejelöljük ( zöld szakasz végpontjai ) és a görbe által határolt területet integrálszámítással, a görbe alatti területek különbségeként számítjuk, az x tengely alatti értékeket szokás szerint negatívnak véve, akkor eredményül a nagy levél területének és a két kis levél területének különbségét kapjuk. Ha OC az y tengellyel  szöget zár be, a kis kék háromszögekből az infinitezimális területdarab szöget zár be, a kis kék háromszögekből az infinitezimális területdarab  Td=4a(cos Td=4a(cos -sin -sin )2acos2 )2acos2   , amiből a teljes terület , amiből a teljes terület
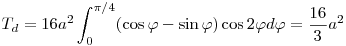
Érdekes, hogy ez a terület a2-nek racionális számszorosa. Elfogadva, hogy a területek abszolút értékének összege
Ts=2 a2 a2
, a felső levél területét T1-gyel, a két kis levél területének összegét T2 -vel jelölve
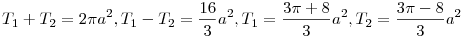
A számértékeket behelyettesítve azt kapjuk, hogy T1 nagyjából 92,5 , T1 pedig 7,5 százaléka a teljes területnek. ( ha jól számoltam ... :-) )
|
 |
| Előzmény: [804] sakkmath, 2009-02-17 13:20:30 |
|
|




 [-
[- ,
, R2 => pn=R1nA+R2nB; (Ha valamit elírtam, javítsatok!)
R2 => pn=R1nA+R2nB; (Ha valamit elírtam, javítsatok!)  <0. Ilyen esetben, hogy lehet felírni az explicit képletet?
<0. Ilyen esetben, hogy lehet felírni az explicit képletet? 






 (X)<+
(X)<+ esetén), hogy a végeredmények rendre +
esetén), hogy a végeredmények rendre +
 szöget zár be, a kis kék háromszögekből az infinitezimális területdarab
szöget zár be, a kis kék háromszögekből az infinitezimális területdarab  a2
a2