| [890] akinom91 | 2009-03-30 23:01:53 |
 Uhh..túl késő van...a könyv szerinti eredmény pi*gyök3/12 lenne. Amúgy megvan a hiba, csak egy mínusz jel volt az egész csúnyaság okozója. (nekem végul pi*gyök2/12 jött ki, nincs is honnan gyök3 legyen benne). Minden esetre köszönöm szépen a válaszolóknak, a szándek számít, ha nem is igazán értettem mindent meg. Van valami trükk, ami mentesít az ilyen béna hibáktól? :)) Jó kérdés...Ha így rontom el az érettsegin is, nézhetem magam. De viccen kívül, valami jó tanácsokat a gyakorlotabbaktól szívesen várok még, sőt lehet kérdésekkel is visszatérek még.
Még egyszer bocsi a fórum fölösleges megtöltéséért, ki is lehet vágni ezeket a megjegyzéseket (én nem kaptam meg, hogyan lehet)
|
| Előzmény: [889] akinom91, 2009-03-30 22:35:05 |
|
| [889] akinom91 | 2009-03-30 22:35:05 |
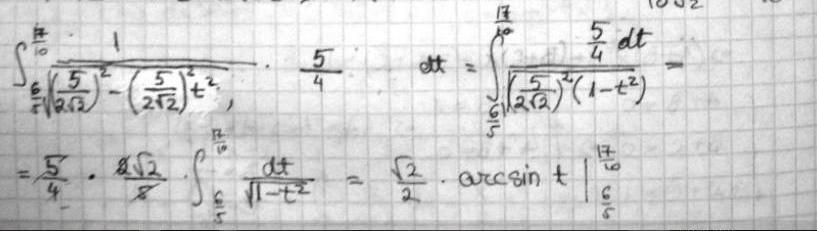
 Na jol van. Akkor kezdjuk az elejen! Oszinten nem igazan ertem miket akarsz mondani, meg matematika egyetemen nem voltam hallgato. Csak egy orult 12-es vagyok, aki azt sem tudja, 3 honap mulva mire felvetelizik. Azt sem tudom mennyire volt ertheto a kerdesem, de most csatolom az en gimnaziumi-szintu megoldasomat (probalkozast), hatha erthetobb lesz. Ha helyes, esetleg folytathato-e valahogy? A tankonyv megoldasnak annyit mond, hogy az eredmeny 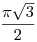 , de en meg csak nem is sejtem, hogy lehet ezt kihozni, innen ahova eljutottam.. :| , de en meg csak nem is sejtem, hogy lehet ezt kihozni, innen ahova eljutottam.. :|
(Bocsanat a sok uzenetert, de csak igy tudtam megoldani a kep csatolasat)
|
 |
|
|
|
| [886] jonas | 2009-03-29 23:55:21 |
 Próbáltad az arkusz szinuszok eredményét (vagy a két eredmény különbségét vagy az argumentumokat) numerikusan kiszámolni, hogy megsejtsd rájuk a kerek formulát, esetleg a Plouffe's Inverter segítségével? Nem számoltam utána, úgyhogy lehet, hogy ez nem működik. Az is lehet persze, hogy tényleg egy csúnya kifejezést kapsz az integrál értékére, amit nem lehet egyszerűsíteni.
|
| Előzmény: [885] akinom91, 2009-03-29 20:40:48 |
|
| [885] akinom91 | 2009-03-29 20:40:48 |
 Igen, igy probaltam, de Newton-Leibniz alkalmazasa utan nagyon csunya lett a 2 arcsin argumentuma, semmi ismeros nem volt. Meg egyszer megoldom, lehet en rontottam valahol, es visszaterek, ha megsem sikerul.
|
| Előzmény: [884] Lóczi Lajos, 2009-03-29 20:16:46 |
|
|
| [883] akinom91 | 2009-03-29 15:31:58 |
 Milyen módszerrel javasoljátok az 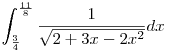 integrál kiszámolását? Illetve milyen helyettesítés a legelőnyösebb? integrál kiszámolását? Illetve milyen helyettesítés a legelőnyösebb?
|
|
|
| [881] jonas | 2009-03-27 16:37:56 |
 Most már otthon vagyok és megnéztem a Szalay: Számelmélet könyvet. Az n=4 esetre leír egy nem túl nehéz elemi megoldást. Az n=3 esetet nem bizonyítja, de megemlíti, hogy az Euler-egészek segítségével látták be.
|
| Előzmény: [877] jonas, 2009-03-27 10:59:51 |
|
|
| [879] R.R King | 2009-03-27 14:36:49 |
 n=3 van az Euler egészekkel. bocsánat
|
|
| [878] R.R King | 2009-03-27 14:36:01 |
 Freud: Számelmélet könyvében benne van az n=4 és az n=3 eset is, de az n=4 Euler-egészekkel (ha jól emlékszem). Gábor azt állította, h az előbbire van középiskolás módszerekkel megoldása. Én szkeptikus vagyok, de ne legyen igazam:) Szerintem egyszer mindenki megkísérli bizonyítani az n=3,4-et aki olvasott gimiben Fermat sejtésről...(aztán az esetek többségében besül a próbálkozás)
|
| Előzmény: [877] jonas, 2009-03-27 10:59:51 |
|
|
|
|
| [874] Gábor1905 | 2009-03-26 22:14:46 |
 Üdv! Csak azt szeretném kérdezni hogy szerintetek gimis matekkal bizonyítható-e a Fermat sejtés n=3 esete?Szerintem sikerült csak még nem írtam le!:D:D:D
|
|
| [873] jenei.attila | 2009-03-23 17:11:37 |
 Továbbra is úgy értelmezem a kérdést, hogy "Hány olyan elem van 64 elemű testben, amely nincs benne valódi résztestben?" Ennek a testnek valóban csak 2,4 és 8 elemű résztestei lehetnek mivel minden test vektortér bármelyik részteste felett, ahogy Fálesz Mihály is írta. Ilyen résztestei pedig valóban vannak is, mégpedig mindegyikből csak 1-1. Ez a test (GF(64)) a x64-x polinomnak felbontási teste (e testben lineáris gyöktényezők szorzatára bomlik), sőt pontosan a x64-x polinom gyökei alkotják a test elemeit. Az, hogy ennek a testnek van 2, 4 és 8 elemű részteste abból következik, hogy a x2-x, x4-x és x8-x polinomok osztói a x64-x polinomnak, amelyek gyökei így szintén GF(64) elemei. Ezek a gyökök könnyen bizonyíthatóan résztesteket alkotnak, mert (x+y)2=x+y,(xy)2=xy,(-x)2=-x,(x-1)2=x-1 (itt kihasználtuk, hogy a test 2 karakterisztikájú). Hasonlóan 4 és 8 kitevővel. Más 2, 4 és 8 elemű résztestei GF(64)-nek nincsenek, mint a most felsorolt polinomok gyökeiből álló testek, mert az azt jelentené hogy a x2-x, x4-x és x8-x polinomoknak 2,4 illetve 8-nál több gyökük lenne ami lehetetlen. A 2 elemű (0,1 -et tartalmazó) résztest részteste a 4 és 8 elemű testeknek is, azonban a 4 elemű résztest nem részteste a 8 eleműnek (mivel a 8 elemű test nem lehet vektortér a 4 elemű felett). Vagyis e résztestek uniója 10 elemet tartalmaz, a maradék 54 elem pedig egyik résztestnek sem eleme.
|
| Előzmény: [862] Bubcsi, 2009-03-17 11:01:41 |
|
| [872] lgdt | 2009-03-20 02:17:01 |
 A Wikipedia szerint ez egy ismert probléma, amelyre eddig nem találtak polinom futásidejű algoritmust, és azt sem tudják, hogy van-e; viszont az inverzét, a hatványozást könnyű hatékonyan elvégezni. Ha jól tudom, az sem ismert, hogy léteznek-e bizonyítottan ilyen tulajdonságú ún. csapóajtófüggvények.
The existence of one-way functions
|
| Előzmény: [867] Borel, 2009-03-18 19:25:53 |
|
|
| [870] Borel | 2009-03-18 21:47:08 |
 Köszönöm a válaszokat. Én is így számoltam eddig, csakhát reméltem van valami hatékonyabb megoldás is... n=7-re a 3 rendjéért már meg kell szenvedni (szg. nélkül).
|
| Előzmény: [869] Tibixe, 2009-03-18 21:03:47 |
|
| [869] Tibixe | 2009-03-18 21:03:47 |
 Végignézheted szép sorban bd-t minden szóba jöhető d-re, azaz amikor d poz. egész és osztja  (n)-t, aztán ha 1 maradékot ad, akkor az aktuális d lesz a válasz. Kis n-re ez is jó. (n)-t, aztán ha 1 maradékot ad, akkor az aktuális d lesz a válasz. Kis n-re ez is jó.
|
| Előzmény: [867] Borel, 2009-03-18 19:25:53 |
|
| [868] R.R King | 2009-03-18 20:26:50 |
 Üdv. Freud: Számelmélet című könyvében pl. utána lehet nézni, de a google is segíthet:) a rend emlékeim szerint a legkisebb ,,jó'' kitevő és osztója minden jó kitevőnek pl. fi(n)-nek is. fi(n) n-ig az n hez relatív prímek száma. Konkrét b és n esetén tehát a rend a fi(n) osztói közül kerül ki. Régen tanultam ezekről talán diszkrét logaritmus(index) címszóval keresd a problémát.
|
| Előzmény: [867] Borel, 2009-03-18 19:25:53 |
|
| [867] Borel | 2009-03-18 19:25:53 |
 Sziasztok!
Egy kis segítségre lenne szükségem: Rn redukált maradékosztályok csoportjában hogy kell elem rendjét kiszámolni? Vagy ami ezzel ekvivalens, b a k-adikon kongruens 1 modulo n egyenletet hogy kell megoldani? (b és n ismert)
Üdv: Borel
|
|
|




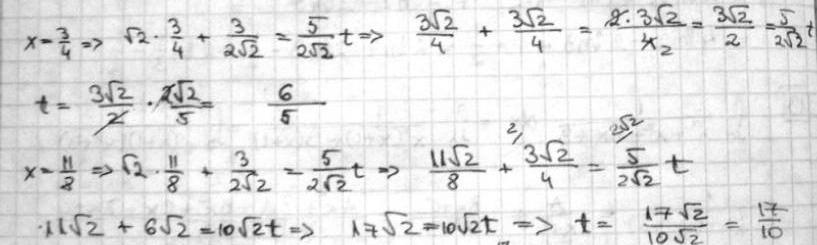



 2mod 7 az nem 1, és 33
2mod 7 az nem 1, és 33
 (n)-t, aztán ha 1 maradékot ad, akkor az aktuális d lesz a válasz. Kis n-re ez is jó.
(n)-t, aztán ha 1 maradékot ad, akkor az aktuális d lesz a válasz. Kis n-re ez is jó.