| [950] Lóczi Lajos | 2009-05-20 11:24:16 |
 Persze a Lebesgue-tétel többi feltételét is ellenőrizni kell, és a szinusz folytonosságát is használva így kijön, hogy az integrálok limesze 0.
A feladat másik részéhez azt vedd észre, hogy a "+1"-es additív tag a nevezőben eltolja a függvényt a 0-tól, így pl. [1/2,1]-en minden  esetén korlátos lesz F. esetén korlátos lesz F.
Vagyis az integrál korlátosságát elég [0,1/2]-en megnézni. Itt viszont a (-2)-odik hatványban a logaritmus fog dominálni (hiszen 0-ban + -hez tart), vagyis az 1 most elhagyható. -hez tart), vagyis az 1 most elhagyható.
Ha   0, akkor mindkét tényező korlátos, vagyis az integrál véges. 0, akkor mindkét tényező korlátos, vagyis az integrál véges.
Ha  =-1, akkor primitív függvénnyel expliciten kiszámolod, hogy az integrál véges. =-1, akkor primitív függvénnyel expliciten kiszámolod, hogy az integrál véges.
Ha   (-1,0), akkor a (-1,0), akkor a 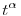 függvény kitevőben való monotonitását használva kapod, hogy az integrál véges. függvény kitevőben való monotonitását használva kapod, hogy az integrál véges.
Ha viszont  <-1, akkor használd fel, hogy a (+1 elhagyása után) a logaritmusos tényező alulról becsülhető egy tetszőlegesen kis kitevőjű t-hatvánnyal [itt lényegében a <-1, akkor használd fel, hogy a (+1 elhagyása után) a logaritmusos tényező alulról becsülhető egy tetszőlegesen kis kitevőjű t-hatvánnyal [itt lényegében a 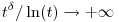 , ha , ha  >0 tetszőleges és t >0 tetszőleges és t + + limesz átrendezéséről van szó], így az integrandus alsó becslése nagyságrendileg limesz átrendezéséről van szó], így az integrandus alsó becslése nagyságrendileg 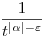 , ahol , ahol  értékét elég kicsinek választva elérhető, hogy a nevező kitevője még mindig 1-nél nagyobb maradjon. Az ilyen hatványfüggvényekről viszont tudjuk, hogy [0,1/2]-en integráljuk divergens, tehát az ilyen értékét elég kicsinek választva elérhető, hogy a nevező kitevője még mindig 1-nél nagyobb maradjon. Az ilyen hatványfüggvényekről viszont tudjuk, hogy [0,1/2]-en integráljuk divergens, tehát az ilyen  számokra az eredeti integrál sem véges. számokra az eredeti integrál sem véges.
|
| Előzmény: [949] Cokee, 2009-05-19 23:42:43 |
|
|
|
|
| [946] Cokee | 2009-05-14 20:26:18 |
 Sziasztok!
Szeretnék segítséget kérni a következő feladatoknál:
Legyen f L1[0,1].Igaz-e,hogy L1[0,1].Igaz-e,hogy ![\sin\bigg(\frac{f(t)}{n}\bigg)\in {L^{1}}[0,1].](keplet.cgi?k=3A6C7B5E90BCCCC3) Számold ki a köv. kettős integrált: Számold ki a köv. kettős integrált: 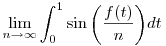
Milyen  esetén integrálható esetén integrálható 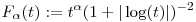 a [0,1] intervallumon? a [0,1] intervallumon?  valós szám. valós szám.
Köszi előre is Cokke
|
|
|
| [944] rizsesz | 2009-05-13 21:34:10 |
 1 helyébe írd be, hogy sin2x+cos2x, rendezz nullára, ossz le sin2x-szel (ami most nem nulla, mert akkor cosx +1 vagy -1, amelyek nem megoldások), így cosx/sinx-ben másodfokú egyenletet kapsz, ahonnan megvan cosx/sinx=ctgx.
|
| Előzmény: [943] fermel, 2009-05-13 21:14:52 |
|
| [943] fermel | 2009-05-13 21:14:52 |
 Sziasztok! A következő triginometriai egyenlet megoldásában kérném a segítségeteket:
2sinxsinx - 5sinxcosx + 7cosxcosx = 1
(Elnézést, de hiába írtam meg Wordben felső index segítségével a szögfüggvények négyzetét, egyszerűen nem másolja át abban a formában, ezért voltam kénytelen így leírni a feladatot)
Köszönöm a segítséget:
fermel
|
|
|
| [941] Kry | 2009-05-06 22:30:14 |
 Sajnos ezt választottam ... Viszont ezt a nem egyforma valószínűséget nem értem . .4 golyónál mért lenne más más a valószínűség mikor ugyan olyan nehéz lenne akaratosan ugyan olyan színűt vagy különböző színűt húzni. És úgylátszik ezt a rész télleg nemértem pedig kombinatorika az egyik kedvencem ...
|
| Előzmény: [940] jenei.attila, 2009-05-06 22:18:51 |
|
| [940] jenei.attila | 2009-05-06 22:18:51 |
 Húha, ezt nagyon nem érted. Ugye ezt a feladatot hagytad ki? A kihúzás sorrendje természetesen nem számít. Vegyünk egy dobozt, amely két piros és két kék golyót tartalmaz. Ha ebből a dobozból két golyót húzol ki, akkor nyilván sokkal valószínűbb hogy különböző színűek lesznek a kihúzott golyók, mint hogy két pirosat, vagy két kéket húzol ki. Egyszerűen azért, mert pl. a két pirosat pontosan el kell találnod, míg különböző színű golyók kihúzásához lehet az egyik vagy másik pirosat, illetve az egyik vagy másik kéket kihúzni. A te logikád szerint pedig csak 3 eset lenne (piros+piros, kék+kék, piros+kék), csak az a baj, hogy ezeknek nem egyenlő a valószínűségük. A kabátos feladatnál is (és minden valszám feladatnál) csak akkor lehet a valószínűség=(kedvező esetek száma)/(összes esetek száma) képlettel számolni, ha az eseteket adó "elemi események" valószínűsége egyenlő. Te olyan elemi eseményeket adtál meg, amelyek valószínűsége nem egyenlő. A valszám feladatokban sokszor az a legnehezebb, hogy megfelelően válasszuk ki az elemi események halmazát, és helyesen állapítsuk meg azok valószínűségét. Csak ezután kezdhetünk a feladat megoldásához.
|
| Előzmény: [939] Kry, 2009-05-06 15:19:56 |
|
| [939] Kry | 2009-05-06 15:19:56 |
 Az idei éretségivel kapcsolatban lenne kérdésem. Pontosan a 18. feladat a) részével ( a feladatsor és javítókulcs http://193.225.13.214/erettsegi2009/ ).
Ha 15 kabátot eggyenlő valószínűséggel választja akkor egyszerre választ 15 kabátot .. tehát nincs sorrendnek lényege. A kérdés is a hibás kabátok menyniségére kérdez rá. Akkor hogy lehet mégis az összes eset 15504, mikor menyiséget nézva csak 6 eset van és a kedvező esetek menyiséget nézve csak 2 van ( 4+11 / 5+10 )
össz eset: 4+11 / 5+10 / 6+9 / 7+8 / 8+7 / 9+6
Előre is kösz
|
|
|
| [937] Janosov Milán | 2009-04-27 14:39:41 |
 Hello! Hallottam (a matektanáromtól) a "dupla derivált" és "dupla integrál" kifejezéseket - de sajnos választ nem azt illetőleg, hogy ezeket az elnevezéseket mikre használják. Az én tippem, hogy két változót tartalmazó függvényeknél. Helyes a tippem?
|
|
| [936] Ágoston | 2009-04-21 16:51:29 |
 Sziasztok! Tudja valaki, hogy csütörtökön hol és mikor lesz az Arany Dani döntő? KÖszi
|
|
| [935] Wesselényi-Garay Andor | 2009-04-19 23:04:54 |
 Sziasztok: a végeredmény http://wergida.blogspot.com/2009/04/babeli-konyvtar.html olvasható. Még egyszer: viszlát, és kösz a halakat, Andor
|
|
| [934] Tibixe | 2009-04-16 20:02:57 |
 Mondok jobbat: 0 és 1 között ott van valahol kanonikusan* kódolva minden lehetséges történet. Aztán harmadikban meg csak húzunk egy vonalat és rábökünk, hogy ez a számegyenes, számok vannak rajta, semmi bonyolult. Micsoda gőg.
* ( mondjuk kettes számrendszer --> bájtok --> UTF-8 )
Egyébként ilyen téren az aduász: Busy beaver function
Ha hiszünk a Wikipediának, akkor minden algoritmikusan definiálható függvénynél gyorsabban nő. Ráadásul magyar találmány.
|
|
| [933] Wesselényi-Garay Andor | 2009-04-16 18:57:17 |
 Kedves Sirpi, nagyon köszönöm!
A bábeli könyvtárban - ahol Borges szerint minden könyv megtalálható - így az én és a Te már megírt, általunk még nem ismert sorsunk is, nos itt egy könyv egy oldalán negyven sor van. A könyvek mindegyike négyszáztíz oldal. Soronként pedig negyven karakter olvasható. A könyvek 25 ortográfiai jelből épülnek fel. Ezeknek a lehetséges kombinációját kerestem. És erre jött ki ez az irdatlan nagy szám. Ami összehasonlíthatatlanul nagyobb mint az univerzumunk.
Mindannyiótoknak még egyszer köszönet, Andor
|
|
| [932] Sirpi | 2009-04-16 09:37:30 |
 Gondolom a Ramsey-tételkört sokan ismeritek (miszerint elég nagy pontszámú gráfban, vagy a komplementerében van elég nagy részgráf). Felmerült bennem, hogy nem csak létezést, hanem darabszámot is megkövetelhetnénk, nevezetesen:
Adható-e jó alsó és felső becslés arra, hogy egy n pontú gráfban, vagy a komplementerében legalább hány háromszög van?
Nem tudom, van-e hivatalos megoldás erre a feladatra, én egy kis progival megnéztem addig, amíg a gép bírta, és azt kaptam, hogy:
| Gráf pontjainak száma (n) |
0 - 5 |
6 |
7 |
8 |
9 |
| Háromszögek minimális száma |
0 |
2 |
4 |
8 |
 12 12 |
|
9-re jelenleg is fut, de ez már órákig eltart. Viszont ezek alapján a számok alapján rákerestem a sorozatra, és ismert az értéke minden n-re (link), szóval megint felfedeztem egy ismert problémát.
|
|
| [931] Sirpi | 2009-04-15 10:25:54 |
 A (kerekítve) 23000-szer nagyobb mint az univerzumunkra írta (jogosan), hogy nem maga a szám nagyobb 23000-szer, hanem a kitevő. Ezt nem is tudom, hogyan lehetne valahogy normálisan érzékeltetni. Talán úgy, hogy képzelj el 23000 db. univerzumot, és mindegyikből kiválasztasz egy atomot. És ahányféleképpen ezt megteheteted, annyi a szám, amit beírtál (ez sokkal-sokkal nagyobb, mint 23000 db univerzum atomjainak száma).
Egyébként gondolom a számod valahogy úgy állt elő, hogy egy könyv max 1,3 millió karakter és egy karakter lehet mondjuk 25 féle.
|
| Előzmény: [929] Wesselényi-Garay Andor, 2009-04-15 00:40:35 |
|
| [930] Sirpi | 2009-04-15 10:01:48 |
 Ha már nagy számoknál tartunk, leírok két módszert nagyon nagy számok (precízebben: hihetetlen gyorsan növő sorozatok) előállítására. Az elsőnek a nevét is tudom, ezek a jól ismert Ackermann-számok:
Vegyünk egy kétváltozós "sorozatot", tehát A(m,n)-et (m,n 1), és legyen A(m,1)=2m (tehát rácsba rendezve az első sor a 2,4,6... sorozat), valamint legyen A(1,n)=2 (tehát az első oszlop csupa 2-es). Ezek után egy még nem ismert A(m,n) elemet úgy számolunk ki, hogy megnézzük, hogy tőle balra mi áll (vagyis A(m-1,n)-et), és a fölötte lévő sor annyiadik elemét írjuk be az (m,n) helyre. Formálisan: 1), és legyen A(m,1)=2m (tehát rácsba rendezve az első sor a 2,4,6... sorozat), valamint legyen A(1,n)=2 (tehát az első oszlop csupa 2-es). Ezek után egy még nem ismert A(m,n) elemet úgy számolunk ki, hogy megnézzük, hogy tőle balra mi áll (vagyis A(m-1,n)-et), és a fölötte lévő sor annyiadik elemét írjuk be az (m,n) helyre. Formálisan:
A(m,n)=A(A(m-1,n),n-1)
Ezek alapján a második sor: 2, 4, 8, 16, 32 (tehát a 2-hatványok)
A 3. sor: 2 4 16 65536 265536 2265536..., a többi sor meg még gyorsabban nő. Nézzétek meg, elég hamar belebotlotok abba, hogy az elemeket már fel se tudjátok írni, mert nincs rá jelölésünk.
Azt mondjuk továbbá, hogy ha van egy sorozatunk, amit ennek a táblázatnak valamelyik (mondjuk k.) sora majorál, akkor a sorozatunk legfeljebb k Ackermann-osztályú.
Ackermann-sorozatnak a főátlót nevezik, ennek nyilván végtelen az Ackermann-osztálya.
* * *
Másik, hasonló konstrukció, ez nem tudom, kinek a nevéhez fűződik:
A számokat úgy jelöljük, hogy veszünk egy számot, és aköré szabályos sokszögeket rajzolunk (koncentrikusan, tehát a sokszögek nem metszik egymást, és van egy egyértelmű sorrendjük kifelé).
Van két kiértékelési szabályunk:
- ha az n szám egy háromszögben van, akkor a háromszöget eltüntetve nn-t írunk be helyette
- ha az n szám egy k-szögben van (k 4), akkor a k-szöget kicseréljük n db. k-1-szögre. 4), akkor a k-szöget kicseréljük n db. k-1-szögre.
Ezek után számoljátok ki, hogy mennyi a 2 egy ötszögben. Elkezdem, hátha valakinek nem világosak a szabályok, és ezáltal azok lesznek (jelölés: 2 3 3 4: a 2-es benne van egy 3-szögben és az egy négyzetben): 4: a 2-es benne van egy 3-szögben és az egy négyzetben):
2 5=2 5=2 4 4 4=2 4=2 3 3 3 3 4=4 4=4 3 3 4=256 4=256 4=... 4=...
* * *
Ezt a két konstrukciót csak azért hoztam fel, mert ebben a modellben az olyan számok, mint amiknek a nagyságrendjét az előző hsz-ekben próbáltátok elképzelni, azok is nagyon picik. Szóval ezeket már tényleg meg se próbáljátok :-)
|
|
| [929] Wesselényi-Garay Andor | 2009-04-15 00:40:35 |
 Sziasztok! Ez rengeteg segítség. Egyetlen kérdésem van már csak. Akkor ez a szám, ami a könyv univerzumának a mérete... hányszor nagyobb a mi univerzumunknál? (Lajos okfejtésében nem értettem valamit...:))
|
|
| [928] Lóczi Lajos | 2009-04-14 22:55:41 |
 De ne úgy írd, hogy "22991-szer nagyobb, mint", mert azt úgy is lehetne érteni, mintha ez a 25-hatvány 22991 db univerzumnyi atommal lenne egyenlő. Szóval, egy ekkora számot nem lehet elképzelni szerintem sehogy :)
|
| Előzmény: [927] Csimby, 2009-04-14 22:05:11 |
|
| [927] Csimby | 2009-04-14 22:05:11 |
 Pár érdekes adat:
Az univerzum mérete: 2280cm3 (legalábbis 1996-ban így saccolták, de mint tudjuk folyamatosan tágul :-)
Az univerzum kora: 259sec
Az univerzumban található atomok száma: 2265 A Föld atomjainak a száma: 2170
Forrás: Schneier, Applied Cryptography (Ha beírod gugliba, hogy "atomok száma az univerzumban", akkor az 5. link egy pdf fájl és abban a 2. oldal)
A te számod tehát  22991-szer nagyobb mint ahány atom van az univerzumban. 22991-szer nagyobb mint ahány atom van az univerzumban.
|
| Előzmény: [926] Wesselényi-Garay Andor, 2009-04-14 21:25:53 |
|
| [926] Wesselényi-Garay Andor | 2009-04-14 21:25:53 |
 Fú nagyon jó fejek vagytok, RETTENETESEN KÖSZÖNÖM és bocsánat, hogy csak most szólok, de nem látom a gépemen automatikusan frissítve az infókat.
Szóval a lehető legpontosabb - legnagyobb számra lenne szükségem - ha ez nem tőrdöfés a matematika szívébe - amit le lehet írni a lehető leghosszabban. Mivel ez egy iszonyat bődületesen nagy szám, ahogy látom itt a számításaitokból, abban is kérem a segítségeteket, hogy ezt hogyan lehet elképzelni? Meghatározni? Hogyan lehet "mérhetővé", illusztratívvá tenni ezt az iszonyat méretű absztrakciót? Teszem azt: a Föld felülete négyzetmilliméterben? Valami hasonló?
Hogy ne áruljak zsákba macskát: Borges Bábeli könyvtárának a méretére vagyok kíváncsi. Ha ezt a számot megkapjuk, akkor - nevessetek ki, de megkapjuk a magasabb rendű negyvenkettőt. A választ a "világmindenség kérdésére", arra, hogy bizonyos peremfeltételek mellett - amit Borghes ebben a gyönyörű esszéjében leír - hány könyvet lehet írni a világon. Kérlek ne nézzetek őrültnek én csak egy egyszerű képletet kaptam annak alapján, amit Borghes leír, de a számítást nem tudom elvégezni!
Andor
|
| Előzmény: [925] Csimby, 2009-04-14 20:41:27 |
|



 esetén korlátos lesz F.
esetén korlátos lesz F.  -hez tart), vagyis az 1 most elhagyható.
-hez tart), vagyis az 1 most elhagyható.  0, akkor mindkét tényező korlátos, vagyis az integrál véges.
0, akkor mindkét tényező korlátos, vagyis az integrál véges.  (-1,0), akkor a
(-1,0), akkor a  >0 tetszőleges és t
>0 tetszőleges és t +
+ értékét elég kicsinek választva elérhető, hogy a nevező kitevője még mindig 1-nél nagyobb maradjon. Az ilyen hatványfüggvényekről viszont tudjuk, hogy [0,1/2]-en integráljuk divergens, tehát az ilyen
értékét elég kicsinek választva elérhető, hogy a nevező kitevője még mindig 1-nél nagyobb maradjon. Az ilyen hatványfüggvényekről viszont tudjuk, hogy [0,1/2]-en integráljuk divergens, tehát az ilyen 
 0(n
0(n


 12
12  3
3
 22991-szer nagyobb mint ahány atom van az univerzumban.
22991-szer nagyobb mint ahány atom van az univerzumban.