|
|
|
| [93] V Laci | 2006-11-18 18:36:36 |
 Köszönöm szépen! Bár jobban örültem volna valamilyen magyar nyelvű leírásnak, így legalább javíthatom az angol-tudásomat is. :)
|
|
|
|
| [90] V Laci | 2006-11-18 15:53:45 |
 Sziasztok! A Minkowski-összegekről szeretnék olvasni. Tudtok ajánlani valamit, ahol utánanézhetnék?
|
|
|
| [88] jonas | 2006-11-17 21:48:39 |
 Az elsőben nem vagyok biztos, mert már nagyon rég használtam deriveot, de ha jól emlékszem, a deriveban a változók alapból valósak, és külön meg kell mondani neki, hogy komplex legyen.
A másodikban azért nem, mert ha egy diák több jutalmat is kap, akkor a másodikban nem számolod 4!-szor. Ha például egy diák között kell szétosztani a négy jutalmat, akkor mindkét esetben csak egy lehetőség van.
|
| Előzmény: [82] phantom_of_the_opera, 2006-11-11 14:55:08 |
|
|
|
| [85] S.Ákos | 2006-11-15 18:55:38 |
 sziisztok! az lenne a kérdésem, hogy (|x|)'=sgnx helyes-e?
|
|
| [84] Hajba Károly | 2006-11-14 09:03:01 |
 Szia Gábor!
Balra fenn az 5 db okker menűpont középső a TeX tanfolyam. Tanulmányozd!
y=Ax2+Bx+C
Az origón átmenő x=3 'függőleges' azaz az y-tengellyel párhuzamos egyenes a parabola szimmetriatengelye. Ebből következik, hogy balra, azaz a negatív irányban amilyen messze van az egyik metszéspont, jobbra, azaz pozitív irányban ugyanolyan messze lesz a másik metszéspont. Azaz x1=0; x2=2*3=6
Mivel az parabola átmegy az origón O(0,0), így a parabola egyik pontja P(x=0,y=0). => 0=A*02+B*0+C. Ez csak akkor igaz, ha C=0. Tehát az egyenletünk y=Ax2+Bx(+0) formára egyszerűsödött. Ismerünk két másik fix pontot is P1(3,-2) és P2(6,0)-t. Ezek segítségével a redukált egyenletből fel tudsz állítani egy kétváltozós kétismeretlenes egyenletrendszert. Ennek elvégzése már nem bonyolult és szerintem te is el tudod végezni.
Kellemes munkát!
|
| Előzmény: [83] Gábor5, 2006-11-13 20:01:51 |
|
| [83] Gábor5 | 2006-11-13 20:01:51 |
 AZ y= a*x*x+b*x+c (az x négyzetet nem engedte máshogy )parabola átmegy az origón, a csúcspontja (3,-2). 1.Határozd meg az x-tengellyel való másik metszéspontot. 2. a; b; c=? Tudna valaki segíteni.
|
|
| [82] phantom_of_the_opera | 2006-11-11 14:55:08 |
 Sziasztok!
Két kérdésem lene:
1. Hogy mondjam meg a Derive-nak, hogy egy komplex szám konjugáltját "felfogja"? Azt szeretném beírni neki, hogy 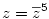 , beírom úgy hogy z=conj(z)5, erre meg leegyszerűsíti nekem úgy, hogy z=z5. , beírom úgy hogy z=conj(z)5, erre meg leegyszerűsíti nekem úgy, hogy z=z5.
2. 28 diáknak osztanak 4 jutalmat. A. egyformák a jutalmak, 1 diák többet is kaphat, ez ismétléses kombináció, 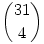 . B. Különböző jutalmak, 1 diák többet is kaphat. A 4 jutalomhoz 28 diákot rendelhetünk, 284. Ha ezt leosztom 4!-sal, a 4 jutalom permutációinak számával, miért nem kapom meg az ismétléses kombinációt? . B. Különböző jutalmak, 1 diák többet is kaphat. A 4 jutalomhoz 28 diákot rendelhetünk, 284. Ha ezt leosztom 4!-sal, a 4 jutalom permutációinak számával, miért nem kapom meg az ismétléses kombinációt?
|
|
| [81] kdano | 2006-10-23 17:00:22 |
 A feladatokat folyamatosan javítják ki a tanév során, az aktuális eredményt itt láthatod: http://www.komal.hu/eredmeny/eredmeny.h.shtml (jelenleg egy feladat sincs kijavítva...)
|
| Előzmény: [80] K. István, 2006-10-23 12:12:07 |
|
| [80] K. István | 2006-10-23 12:12:07 |
 Hello! Idén jelentkeztem először a KöMaLra. Hol lehet megnézni a pontveseny eredményeit? Vagy csak év végén lehet egyben?
|
|
| [79] Matthew | 2006-06-11 11:48:07 |
 hogyan kell ábrát készíteni a grafi-logikai feladványokhoz?
Máté
|
|
| [78] Joaquin | 2006-06-02 19:58:18 |
 elnézést júliust akrtam írni
|
|
| [77] Joaquin | 2006-06-02 19:56:16 |
 érdeklődni szeretnék, hogy a kömal nyári fizika tábor mikor lesz idén, úgy mint tavaly június elején vagy máskor?
|
|
| [76] Cybernaut | 2006-03-25 21:31:16 |
 Köszi szépen!
Erre nem gondoltam. Persze értem a hatványozás alapját, meg a nevezetes azonosságokat is, csak ebben az alakban nem írtam fel. Egyszóval túlkomplikáltam.
Mégegyszer köszi!
|
| Előzmény: [75] Doom, 2006-03-25 19:51:48 |
|
| [75] Doom | 2006-03-25 19:51:48 |
 Ööö nem biztos hogy értem a problémádat, de ha erre gondoltál:
Mivel a3 azt jelenti, hogy a*a*a, így a3=a*a2. Ezt alkalmazva jelen estben is, majd az (n+1)-es szorzót felbontva épp az eredeti azonosság jobb oldalát kapod...
(n+1)3=(n+1)[(n+1)2]=n(n+1)2+(n+1)2
|
| Előzmény: [74] Cybernaut, 2006-03-25 19:07:01 |
|
| [74] Cybernaut | 2006-03-25 19:07:01 |
 Sziasztok!
Az
(n+1)3 = n(n+1)2+(n+1)2
egyenlet megértésében tud valaki segíteni?
Nem tudtam rájönni, hogy az egyenlet jobb oldala milyen összefüggéseken alapul. Miből lehet ezt levezetni?
Azért is hálás lennék ha tudnátok írni olyan linket ahol utána lehet olvasni.
Előre is köszi!
|
|
|
|










