|
| [2244] Lpont | 2021-04-21 16:01:54 |
 Valóban, a KH-nak van 102 és 104 kezdetű azonosítója, sőt a CIB-nek is létezik 107 és 111 kezdetű bankszámlaszáma, és az Erste-t elírtam, helyesen 116.
Bár ezek után a fene se érti...........
|
| Előzmény: [2243] Berko Erzsebet, 2021-04-21 04:10:05 |
|
| [2243] Berko Erzsebet | 2021-04-21 04:10:05 |
 Én is hasonló témával foglalkozom mostanság. Egy összeget kellett befizetnem, átutalnom. Megkaptam a számlaszámot. A neten utánanéztem a banknak. Hogy olcsóbb legyen, oda mentem: KH. (Remélem, így is van.) Azért írok, mert KH, és nem 104-gyel kezdődik, hanem 102-vel.
|
|
|
| [2241] Lpont | 2021-04-20 12:25:42 |
 Még egyszerűbb az azonosítás: az első három számjegy a bankot (pl. OTP:117, KH:104, Erste:106, CIB:107), a következő négy számjegy a fiókot azonosítja, a 8. számjegy az ellenőrző szám.
A 9-16 vagy 9-24 számjegyek az ügyfelet azonosítják, míg a 16. vagy 24. szintén ellenőrző szám.
|
| Előzmény: [2240] Erben Péter, 2021-04-20 07:42:05 |
|
| [2240] Erben Péter | 2021-04-20 07:42:05 |
 Ez az oldal azt mondja, hogy 24-jegyű számlaszámoknál csak két ellenörző kód van (ami úgy működik, ahogy írtad), az első 7 jegy után egy, majd a következő 15 jegy után a második.
Így nekem az jött ki, hogy a három felsorolt szám tényleg helyes. Egy online kereső meg is mondja (az első 8 jegy alapján), hogy melyik bankokról van szó.
|
| Előzmény: [2239] marcius8, 2021-04-17 18:29:49 |
|
| [2239] marcius8 | 2021-04-17 18:29:49 |
 Hátha van itt olyan valaki, aki banki dolgokban járatos. Szóval a bankszámlaszámok 2 vagy 3 darab 8jegyű számból állnak. Én úgy tudom, hogyha egy ilyen 8jegyű szám \(\displaystyle abcdefgh\) alakú, akkor a következő mennyiségnek 0-ra kell végződnie:
\(\displaystyle 9a+7b+3c+1d+9e+7f+3g+1h\)
Tekinthetnénk ezt egy bankszámlaszám érvényességét eldöntő algoritmus ak is. Igen ám, csakhogy találkoztam olyan számlaszámokkal, ahol az azokban lévő 8jegyű számokra az előbbi összefüggés nem teljesül, ugyanakkor internetes oldalon, ahol lehet számlaszámok érvényességét ellenőrizni, az a jelzés érkezik, hogy ezek a számlaszámok érvényesek, technikailag helyesek, pénzcorgalom is van rajtuk, de nem biztos, hogy bankszámlaszámok. Ilyen számok a következők:
10402623-82484855-48511029
10400061-86768370-86551002
10300002-13210936-00014905
Ezek után, ha ezek a számlaszámok nem bankszámlaszámok, akkor milyen számok? Illetve egy bankszámlaszámól hogyan lehet eldönteni, hogy érvényes, ha az általam említett ellenőrzési algoritmus nem jó?
|
|
| [2238] nadorp | 2020-07-20 09:17:40 |
 Nem gondolom,hogy ez Neked "Valaki mondja meg" téma, inkább "Híres(?) álbizonyítások" közé való. Az \(\displaystyle x^3=1\) egyenletig nincs is baj, de ennek 3 gyöke van a komplex számok között, míg az eredi egyenletnek - másodfokú lévén - csak kettő, ráadásul mindkettő harmadik komplex egységgyök. A "bizonyításod" csak arról szól, hogy a valós számok halmazán nincs az eredeti egyenletednek gyöke. Nem a 3=0 azonosságot bizonyítottad be, hanem ellentmondásra jutottál azzal a feltevéssel, hogy a másodfokú egyenletnek van valós gyöke.
|
| Előzmény: [2237] marcius8, 2020-07-16 14:54:39 |
|
| [2237] marcius8 | 2020-07-16 14:54:39 |
 Tétel: \(\displaystyle 3=0\)
Bizonyítás: Megoldandó a következő egyenlet:
\(\displaystyle x^2+x+1=0\)
1. MÓDSZER:
A megoldandó egyenlet mindkét oldalából elvéve \(\displaystyle x\)-et és \(\displaystyle 1\)-et:
\(\displaystyle x^2=−x−1\)
2. MÓDSZER:
A megoldandó egyenlet mindkét oldalát \(\displaystyle x\)-el osztva, ugyanis biztos, hogy \(\displaystyle x\) értéke nem lehet \(\displaystyle 0\):
\(\displaystyle x+1+\frac{1}{x}=0\)
Mindkét oldalból elvéve \(\displaystyle x\)-et és \(\displaystyle 1\)-et:
\(\displaystyle \frac{1}{x}=−x−1\)
ÖSSZEGZÉS: Tehát a megoldandó egyenletből kiindulva két olyan egyenlet adódott a két módszer során, amelyek jobb oldalán ugyanaz az \(\displaystyle −x−1\) kifejezés szerepel, így ennek a két egyenletnek a bal oldala is egyenlő, azaz:
\(\displaystyle x^2=\frac{1}{x}\)
Szorozva \(\displaystyle x\)-el ennek az egyenletnek mindkét oldalát:
\(\displaystyle x^3=1\)
Mindkét oldalból köbgyököt vonva:
\(\displaystyle x=1\)
Behelyettesítve a megoldandó egyenletbe az \(\displaystyle x=1\) kapott értéket:
\(\displaystyle 1^2+1+1=0\)
összevonás:
\(\displaystyle 3=0\)
|
|
| [2234] marcius8 | 2020-03-23 22:00:57 |
 Útmutatás: Ha ábrázolod az \(\displaystyle f_0(x)\), \(\displaystyle f_1(x)\), \(\displaystyle f_2(x)\), \(\displaystyle f_3(x)\), \(\displaystyle f_4(x)\), \(\displaystyle f_5(x)\), ..... függvényeket, észreveszed, hogy a grafikonok milyen szabályosság szerint követik egymást.
|
| Előzmény: [2232] jsmit654, 2020-03-15 12:19:06 |
|
| [2232] jsmit654 | 2020-03-15 12:19:06 |
 \(\displaystyle f_0(x)=|x|, f_n(x)=|f_{n-1}(x)-1|, f_{22221}(22221.1)=?\)
|
|
| [2231] nadorp | 2020-02-29 23:30:51 |
 Ha már integráltunk,akkor deriváljunk is. Az alábbi megoldás egy kicsit számolósab ("ijesztőbb" :-), direktben megadja az \(\displaystyle X=\max_iX_i\) valószínűségi változó eloszlását és ennek generátorfüggvénye alapján számoljuk a várható értéket.
Szükség lesz az \(\displaystyle f(x)=\prod_{i=1}^{n}(e^{p_ix}-1)\) függvény alábbi tulajdonságaira:
\(\displaystyle f{'}(x)-f(x)=\sum_{i=1}^np_i\prod_{j\neq i}(e^{p_jx}-1)\tag1\)
Ha f(x) Taylor-sora \(\displaystyle f(x)=\sum_{k=0}^\infty a_kx^k\), akkor mivel 0 n-szeres gyöke f-nek
\(\displaystyle a_0=...=a_{n-1}=0 \tag2\)
\(\displaystyle f{'}(x)-f(x)=\sum_{k=n}^\infty(ka_{k}-a_{k-1})x^{k-1} \tag3\)
Legyen \(\displaystyle q_k=P(X=k)\). Ekkor nyilván \(\displaystyle q_0=...=q_{n-1}=0\) továbbá a \(\displaystyle G(x)=\sum_{k=n}^\infty q_kx^k\) generátorfüggvény felhasználásával \(\displaystyle E(X)=G{'}(1)\), így elég G'(1) értékét meghatározni.
Ha X=k és utoljára az i értéket húztuk, továbbá a többi j érték \(\displaystyle x_j\)-szer fordult elő (\(\displaystyle x_j\geq1,j\neq i\)), akkor ez az esemény \(\displaystyle \frac{(k-1)!}{\prod{x_j!}}\) esetben fordul elő és minden előfordulás valószínűsége \(\displaystyle p_i\prod p_j^{x_j}\) Tehát
\(\displaystyle q_k=\sum_{i=1}^{n}
\sum_{\begin{matrix} \sum x_j=k-1\\
j\neq i\\
x_j\geq1
\end{matrix}}
p_i\prod p_j^{x_j}\frac{(k-1)!}{\prod {x_j!}}=(k-1)!\sum_{i=1}^{n}p_i
\sum_{\begin{matrix}
\sum x_j=k-1\\
j\neq i\\
x_j\geq1
\end{matrix}}
\prod\frac{p_j^{x_j}}{{x_j!}}\)
Látható, hogy \(\displaystyle \frac{q_k}{(k-1)!}\) értéke megegyezik az (1) jobb oldalán szereplő függvény Taylor-sorában az \(\displaystyle x^{k-1}\) tag együtthatójával, így (3) szerint
\(\displaystyle q_k=(k-1)!(ka_k-a_{k-1})=k!a_k-(k-1)!a_{k-1}=f^{(k)}(0)-f^{(k-1)}(0) \tag4\)
Ha \(\displaystyle F(x)=\sum_{k=n}^\infty f^{(k)}(0)x^k\) (a definíció érvényes |x|<1 esetben, hiszen \(\displaystyle \lim_{k\to\infty} f^{(k)}(0)=\sum q_k=1\)), akkor (4) alapján \(\displaystyle G(x)=F(x)(1-x)\). De \(\displaystyle f^{(k)}(0)\) könnyen számolható, ha f(x) definíciójában elvégezzük a tagonkénti szorzást.
Legyen \(\displaystyle S_i\) a \(\displaystyle \{p_1,...,p_n\}\) halmaz i elemű részhalmazainak a halmaza és tetszőleges \(\displaystyle S\in S_i\) esetén legyen \(\displaystyle |S|=\sum_{p_i\in S}p_i\). Ekkor \(\displaystyle k\geq1\) esetén
\(\displaystyle f^{(k)}(0)=1-\sum_{S\in S_{n-1}}|S|^k+
\sum_{S\in S_{n-2}}|S|^k-...+(-1)^{n-1}\sum_{S\in S_1}|S|^k=1+\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}|S|^k \tag5\)
Felhasználva, hogy (5)-ben mindenhol |S|<1, F(x) hatványsorában |S|x hányadosú mértani sorokat kell összegeznünk, így
\(\displaystyle F(x)=\frac{x^n}{1-x}+\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}\frac{|S|^nx^n}{1-|S|x}\)
\(\displaystyle G(x)=x^n+(1-x)\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}\frac{|S|^nx^n}{1-|S|x}\)
\(\displaystyle E(X)=G{'}(1)=n-\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}\frac{|S|^n}{1-|S|}=n-\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}\left(\frac{|S|^n-1}{1-|S|}+\frac1{1-|S|}\right)\)
Felhasználva, hogy ha \(\displaystyle S\in S_i\), akkor egyértelműen megfeleltethető neki egy olyan \(\displaystyle S'\in S_{n-i}\), hogy 1-|S|=|S'|, kapjuk
\(\displaystyle E(X)=n-\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}\frac{|S|^n-1}{1-|S|}-\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_{n-i}}\frac1{|S|}\)
\(\displaystyle E(X)=n+\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}(|S|^{n-1}+|S|^{n-2}+...+1)+\sum_{i=1}^{n-1}(-1)^{i+1}\sum_{S\in S_i}\frac1{|S|} \tag6\)
Alkalmazzuk most (5)-öt a k=1,2,...n-1 esetben és adjuk össze az egyenlőségeket. Mivel most \(\displaystyle f^{(k)}(0)=0\), kapjuk
\(\displaystyle 0=\sum_{k=1}^{n-1}f^{(k)}(0)=n-1+\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}(|S|^{n-1}+|S|^{n-2}+...+|S|)\)
Ebből azonnal következik, hogy (6)-ban
\(\displaystyle n+\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}(|S|^{n-1}+|S|^{n-2}+...+1)=1+\sum_{i=1}^{n-1}(-1)^{n-i}\sum_{S\in S_i}1=1+\sum_{i=1}^{n-1}(-1)^{n-i}\binom{n}{i}=(-1)^{n+1}\)
Tehát
\(\displaystyle E(X)=(-1)^{n+1}+\sum_{i=1}^{n-1}(-1)^{i+1}\sum_{S\in S_i}\frac1{|S|}=\sum_{i=1}^{n}(-1)^{i+1}\sum_{S\in S_i}\frac1{|S|}\)
|
| Előzmény: [2230] Erben Péter, 2020-02-28 09:46:35 |
|
| [2230] Erben Péter | 2020-02-28 09:46:35 |
 Meglepő és szép ez az integrálos átírás. Ha jól látom, két kevésbé közismert összegzési formula is kijön belőle, ha az eredeti szummás alakba behelyettesítjük az \(\displaystyle \frac{1}{n}\) és \(\displaystyle \frac{2}{n}\) valószínűségeket.
Amikor minden valószínűség egyenlő:
\(\displaystyle E = \sum _{k=1}^{n} (-1)^{k+1} \binom{n}{k} \cdot \frac{n}{k} = n\cdot\left(1+\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{n}\right)\)
Innen:
\(\displaystyle \sum _{k=1}^{n} (-1)^{k+1} \binom{n}{k} \cdot \frac{1}{k} = 1+\frac{1}{2}+\frac{1}{3}+\dots +\frac{1}{n}\)
A második esetben pedig két részre bontható az összeg. Az első rész megfelel az előző esetnek (\(\displaystyle n-2\) taggal), így a második tagok összegére kapunk összefüggést.
\(\displaystyle E = \sum _{k=1}^{n} (-1)^{k+1} \left(\binom{n-2}{k} \cdot \frac{n}{k} + \binom{n-2}{k-1} \cdot \frac{n}{k+1}\right)= n\cdot\left(1+\frac{1}{2}+\frac{1}{3}+\dots+\frac{1}{n-1} - \frac{1}{n}\right)\)
Áttérve \(\displaystyle n-2\)-ről \(\displaystyle n\)-re és a zárójelek első tagjait a korábbi képlettel összegezve innen azt kapjuk, hogy
\(\displaystyle \sum _{k=0}^{n} (-1)^{k} \binom{n}{k} \cdot \frac{1}{k+2}= \frac{1}{n+1} - \frac{1}{n+2}\)
|
| Előzmény: [2229] Fálesz Mihály, 2020-02-26 11:00:58 |
|
| [2229] Fálesz Mihály | 2020-02-26 11:00:58 |
 A [2224]-beli képletnek van egy vicces átírása integrálokkal:
\(\displaystyle
\sum_i\frac1{p_i}-\sum_{i<j}\frac1{p_i+p_j}+\sum_{i<j<k}\frac1{p_i+p_j+p_k}-+\ldots+(-1)^{n-1}\frac1{p_1+\ldots+p_n} =
\)
\(\displaystyle
= \int_0^1 \left(
\sum_i x^{p_i-1} -\sum_{i<j} x^{p_i+p_j-1}
+\sum_{i<j<k} x^{p_i+p_j+p_k-1}
-+\ldots+(-1)^{n-1}x^{p_1+\ldots+p_n-1}
\right)\mathrm{d}x =
\)
\(\displaystyle
= \int_0^1 \left(1-\prod_{i=1}^n(1-x^{p_i})\right) \frac{\mathrm{d}x}{x}.
\)
Ha \(\displaystyle p_1=\ldots=p_n=\frac1n\), akkor az \(\displaystyle x=(1-y)^n\) helyettesítéssel
\(\displaystyle
\ldots = n\int_0^1 \frac{1-y^n}{1-y} \mathrm{d}y
= n\int_0^1\big(1+y+y^2+\ldots+y^{n-1}\big) \mathrm{d}y
= n\bigg(1+\frac12+\frac13+\ldots+\frac1n\bigg).
\)
Ha csak \(\displaystyle n-1\) valószínűség van, \(\displaystyle p_1=\ldots=p_{n-2}=\frac1n\) és \(\displaystyle p_{n-1}=\frac2n\), akkor, ugyanazzal a helyettesítéssel
\(\displaystyle
...
= n\int_0^1 \frac{\big(1-y^{n-2}(2y-y^2)\big)}{1-y} \mathrm{d}y
= n\int_0^1\big(1+y+y^2+\ldots+y^{n-2}-y^{n-1}\big) \mathrm{d}y =
\)
\(\displaystyle
= n\bigg(1+\frac12+\frac13+\ldots+\frac1{n-1}-\frac1n\bigg).
\)
Ebből is leolvasható, hogy a különbség éppen \(\displaystyle 2\).
(jonas [2227]-ből is látszik, egyszerűbben és kevésbé ijesztően.)
|
| Előzmény: [2228] Erben Péter, 2020-02-25 17:52:37 |
|
|
| [2227] jonas | 2020-02-25 14:16:57 |
 Valóban várhatóan 127/10 = 12.7 dobás kell.
Közönséges 6 oldalú kockánál várhatóan \(\displaystyle 6/6 + 6/5 + 6/4 + 6/3 + 6/2 + 6/1 \) dobás kell, hogy mind a 6 oldal előjöjjön. Ha már öt oldalt kidobtunk, akkor a hatodik átlagosan 6 dobásból jön ki.
A huncut kockánál különböztessük meg továbbra is a hat oldalt egymástól. Várhatóan \(\displaystyle 6/6 + 6/5 + 6/4 + 6/3 + 6/2 \) dobás kell ahhoz, hogy öt oldal előjöjjön, és addig biztosan dobálni kell a kockát. Ekkor a kocka minden oldalára egyformán 1/6 a valószínűsége, hogy pont az az oldal nem fordult még elő. 2/6 valószínűséggel tehát ez az oldal valamelyik 5 pontos oldal: ebben az esetben már öt szám előjött, és nem kell tovább dobnunk. 4/6 valószínűséggel valami más a kimaradó oldal, mert már mindkét ötös oldalt láttuk: ekkor tovább kell dobni, amíg a kimaradó egy oldal is előjön, vagyis átlagosan még \(\displaystyle 6/1 \) dobásig. Ez összesen átlagosan \(\displaystyle 6/6 + 6/5 + 6/4 + 6/3 + 6/2 + 4/6\cdot6/1 \) dobás, ez pedig \(\displaystyle 127/10 \).
|
|
| [2226] marcius8 | 2020-02-24 19:28:48 |
 megint tanultam valami újat. köszi. Egyébként ez egy bűvésztrükk matekos részéhez kellett. A trükk lényege, hogy ezzel a cinkelt kockával választok ki hat kártyából a második kártyát, mégpedig úgy hogy azt nem dobom ki a cinkelt kockával. Ha olyan lenne a cinkelt kocka, hogy rögtön és mindig 2-est hozza ki, na az gyanús lenne. De így nem az.
|
| Előzmény: [2224] Erben Péter, 2020-02-24 19:02:49 |
|
|
| [2224] Erben Péter | 2020-02-24 19:02:49 |
 A feladat a kupongyűjtő probléma azon esete, amikor a valószínűségek nem egyenlők.
A cinkelt dobókockával való dobás megfeleltethető egy kupon megvásárlásának. Tegyük fel, hogy \(\displaystyle n\) különböző ,,kupon'' létezik, amelyek \(\displaystyle p_1\), \(\displaystyle p_2\), ..., \(\displaystyle p_n\) valószínűséggel fordulnak elő (ahol \(\displaystyle p_1+\ldots+p_n=1\)). Célunk, hogy egy teljes kupon-gyűjteményt állítsunk össze, és kérdésünk, hogy várhatóan hány kupont kell ehhez megvennünk.
A konkrét feladatban \(\displaystyle n=5\), a valószínűségek pedig \(\displaystyle \frac{1}{6}\), \(\displaystyle \frac{1}{6}\), \(\displaystyle \frac{1}{6}\), \(\displaystyle \frac{1}{3}\), \(\displaystyle \frac{1}{6}\).
Az általános feladat megoldása megtalálható például Marco Ferrante és Monica Saltalamacchia The Coupon Collector’s Problem című írásában.
(Vázlatosan.) Jelentse az \(\displaystyle X_i\) valószínűségi változó azt, hogy hányadik húzásnál kaptuk meg először az \(\displaystyle i\) értéket. (Az egyszerűség kedvéért mostantól feltételezzük, hogy az 1,2,...,\(\displaystyle n\) értékek jöhetnek ki. Ez a feltételezés olvashatóbbá teszi az indexeket, és nem változat a feladat lényegén.)
A fenti jelöléssel a teljes gyűjteményt \(\displaystyle \max_{i\in \{1,\ldots,n\}} X_i\) lépésben állítjuk össze. Keressük \(\displaystyle \max X_i\) várható értékét.
Felhasználjuk a skatulya-elvhez analóg alábbi azonosságot:
\(\displaystyle
\max_{i}\{x_i\}
=\sum_{i=1}^n x_i - \sum_{i<j}\min\{x_i,x_j\} +\sum_{i<j<k}\min\{x_i,x_j,x_k\} - \cdots + \left(-1\right)^{n+1}\min\{x_1,\ldots,x_n\},
\)
továbbá a várható érték linearitását.
\(\displaystyle
E[\max X_i]
= \sum E[X_i] - \sum_{i<j} E[\min\{X_i, X_j\}] + \sum_{i<j<k} E[\min\{X_i,X_j,X_k\}] - \ldots
\)
Vegyük még észre, hogy az \(\displaystyle X_i\), \(\displaystyle \min\{X_i,X_j\}\), \(\displaystyle \min\{X_i,X_j,X_k\}\), ...valószínűségi változók mind geometriai eloszlásúak, rendre \(\displaystyle p_i\), \(\displaystyle p_i+p_j\), \(\displaystyle p_i+p_j+p_k\), ...paraméterrel.
Például \(\displaystyle \min\{X_1, X_2\}\) azt jelenti, hogy mikor jött ki először egy kupon az \(\displaystyle \{1,2\}\) halmazból, vagyis mikor következett be először egy \(\displaystyle p_1+p_2\) valószínűségű esemény.
Mivel a \(\displaystyle p\) valószínűségű esemény első bekövetkezésének várható értéke \(\displaystyle \frac{1}{p}\), ezért a kupongyűjtő probléma megoldása:
\(\displaystyle
E[\max X_i] = \sum_{i}\frac{1}{p_i}- \sum_{i<j}\frac{1}{p_i+p_j} + \sum_{i<j<k}\frac{1}{p_i+p_j+p_k}-\ldots+(-1)^{n+1}\frac{1}{p_1+\ldots+p_n}
\)
A cinkelt kockára mondjuk \(\displaystyle p_1=p_2=p_3=p_4=\frac{1}{6}\) és \(\displaystyle p_5=\frac{1}{3}\). Alkalmazva a fenti formulát a keresett várható lépésszámra \(\displaystyle \frac{127}{10}\) jön ki.
|
| Előzmény: [2223] marcius8, 2020-02-24 18:55:55 |
|
|
|
| [2221] marcius8 | 2020-02-20 20:09:00 |
 Van egy szabályos dobókockám, minden lapjára egyforma valószínűséggel esik. Kicsit huncut vagyok, és a 2-es oldalt átváltoztatom 5-ösre. Így a kockán lesz két 5-ös oldal, de nem lesz 2-es oldal. Addig dobok a kockával, amíg az 1, 3, 4, 5, 6 számok mindegyike előkerül. Mennyi lesz a dobások számának várható értéke?
|
|
|
| [2218] sakkmath | 2019-11-21 01:56:56 |
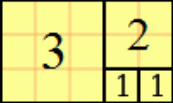
 Javallott tanulmányozni a GOOGLE (kép)találatait a "Fibonacci spirál" beírására.
Mindkét ábra hibája az, hogy a négyzetekbe rajzolandó Fibonacci spirál megszakad (a két ábrán más-más helyen), s így a Fibonacci számok sorrendjét már nem követi a két ábra. A két hiba úgy javítható, hogy a rossz helyekre került négyzeteket áthelyezzük a megfelelő helyekre.
1)
http://talaldki.com/wp-content/uploads/2017/11/Fibonacci3.jpg esetében a megoldás: A legnagyobb négyzetet kivágjuk és eltoljuk jobbra, vízszintesen, \(\displaystyle 55+34=89\) egységgel. Ebben az új helyzetben a 34 oldalhosszúságú négyzet jobb alsó sarkába érkező Fibonacci spirál már át tud lépni az áthelyezett legnagyobb négyzetbe.
2)
http://talaldki.com/wp-content/uploads/2018/08/Fibonacci6.jpg, erre pedig lásd az alábbi, kijavított ábrarészletet:
|
 |
| Előzmény: [2217] SmallPotato, 2019-11-21 00:24:37 |
|
| [2217] SmallPotato | 2019-11-21 00:24:37 |
 Amennyire látom, a két ábra ugyanaz. "Állítás" nincs bennük, szóval "hiba" se igazán lehet (filozófusok bizonyára pontosítanának ...); mindenesetre amit sugallnak, hogy ugyanis Fibonacci-számok folyamatos sorozatával egyező oldalhosszúságú négyzetekkel hézagmentesen le lehet fedni a sík tetszőlegesen nagy darabját, az számomra igaznak tűnik.
Kíváncsi vagyok, milyen "hibát" lehet találni bennük. (Hogy a négyzetek a jpg-ben nem pontosan négyzetesre sikerültek, az, gondolom, nem számít ide)
|
| Előzmény: [2216] sereva, 2019-11-19 22:51:34 |
|









