| [2331] SmallPotato | 2024-02-23 18:08:30 |
 Erre azért tényleg kíváncsi vagyok most már magam is.
(a határérték felhasználása nélküli megoldásokról az a közismert "bizonyítás" jut eszembe, amely szerint a négyzet átlója az oldalak összegével egyenlő)
|
| Előzmény: [2329] marcius8, 2024-02-20 05:03:35 |
|
|
| [2329] marcius8 | 2024-02-20 05:03:35 |
 Köszönöm az eddigi segítségeket. A legutóbbi hsz-omból kimaradt egy "ne". Tehát javítva: Hogyan lehet meghatározni egy parabola alatti területet, hogy az eljárásban NE legyen végtelen sor és NE legyen határérték, és NE legyen differenciálszámítás vagy integrálszámítás, mert hogy ezek nem elemi módszerek.
|
| Előzmény: [2326] marcius8, 2024-02-19 14:29:54 |
|
|
|
| [2326] marcius8 | 2024-02-19 14:29:54 |
 Parabola alatti területet hogyan lehet meghatározni teljesen elemi módszerekkel, azaz az eljárásban legyen benne végtelen sor határértéke, és ne legyen integrálszámítás? Előre is köszönök minden segítséget.
|
|
| [2324] marcius8 | 2024-01-11 21:50:01 |
 Érdekelne az is, hogy rendezett állapotból kiindulva, megengedett cseréket végrehajtva, a kártyalapok milyen permutációja érhető el. Előre is köszönöm mindenki segítségét.
|
| Előzmény: [2323] marcius8, 2024-01-11 20:45:17 |
|
| [2323] marcius8 | 2024-01-11 20:45:17 |
 Eredeti megfogalmazásomban a következőképpen nézett ki az előbb felvetett probléma, amelyet Kós Géza Tanár Úr átfogalmazott, és a KöMaL-pontversenybe került be: (érdekes matek feladatok, [3668], Kömal, 2013 március, "A" feladatok)
Egy játékot találtam ki. Mivel egy játékkal akkor foglalkoznak sokan, ha szabályai egyszerűek, ugyanakkor nem könnyen végigjátszható, ezért a következő játékot találtam ki:
A magyar kártyacsomag összetétele: A magyar kártyacsomag 32 lapot tartalmaz. Minden lapnak van színe és értéke. A színek lehetnek: „piros” (tavasz), „tök” (nyár), „zöld” (ősz), „makk” (tél). Az értékek lehetnek: „VII”, „VIII”, „IX”, „X”, „alsó”, „felső”, „király”, „ász”. A kártyacsomagban minden lehetséges szín-érték párosítás előfordul.
A nyolc sorból és négy oszlopból álló táblázatban elhelyezett magyar kártyacsomag lapjai akkor vannak rendezett sorrendben, ha a következő feltételek teljesülnek:
• A táblázat minden oszlopában található négy lap színének sorrendje felülről lefelé haladva: „piros” (tavasz), „tök” (nyár), „zöld” (ősz), „makk” (tél).
• A táblázat minden sorában található nyolc lap értékének sorrendje balról jobbra haladva: „VII”, „VIII”, „IX”, „X”, „alsó”, „felső”, „király”, „ász”.
A játék szabálya: A kártyacsomag lapjai véletlenszerű sorrendben egy négy sorból és nyolc oszlopból álló táblázatban vannak elhelyezve. A játék során egyszerre mindig két lapot lehet megcserélni. Két lapot csak akkor lehet megcserélni, ha a két lap ugyanabban a sorban vagy ugyanabban az oszlopban van, továbbá (és) ha a két lap színe vagy értéke ugyanaz. A játék célja, hogy a kártyalapok sorrendje rendezett legyen.
Az érdekes az hogy a véletlenszerűen összekevert állapotból majdnem mindig abba az állapotba jutok, hogy a rendezett állapothoz képest a "makk ász" és a "tök király" fel van cserélve. Sajnos, nem tudok rájönni, hogy ez az én ügyetlenségem (gyanítom, hogy igen), de ugyanakkor nem hiszem hogy ennek törvényszerűen így kell lenni. Arra kérek bárkit, hogy ha ezt a jelenséget meg tudja indokolni, vagy meg tudja oldani (tehát ha a rendezett állapothoz képest csak a "makk ász" és a "tök király" van felcserélve, akkor ez az állapot rendezhető vagy sem), írjon a zoltanbertalan680308@gmail.com címre.
|
|
|
| [2321] Lpont | 2023-12-17 08:49:00 |
 Tűzzük ki nehezített változatban a feladatot.
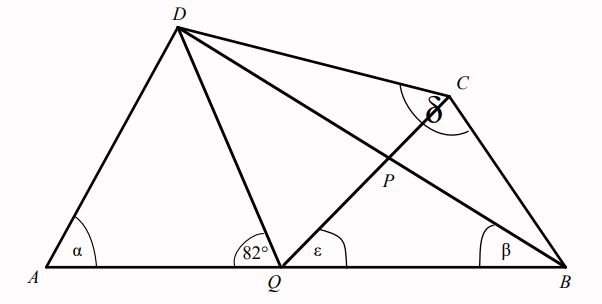
Létezik-e olyan nem elfajuló konvex QBCD négyszög melynek Q-nál és D-nél levő szögei rendre 98 és 16fok, továbbá QD=DC, CQ=QB és a keresett négyszög átlóinak P metszéspontjára teljesül a PB=BC feltétel.
a) Ha van ilyen négyszög, akkor határozzuk meg a hiányzó szögeit.
b) Indokoljuk, ha nincs ilyen tulajdonságú négyszög.
|
| Előzmény: [2316] BerkoErzsebet, 2023-12-16 22:32:57 |
|
| [2320] Lpont | 2023-12-17 00:29:59 |
 Javítom magam......
Ha Q felezi AB-t, akkor sem jó az ábra és nem oldható meg a feladat, mert DBC háromszögben D-nél 0 fok kell legyen, ha a kiindulási feltételek teljesülnek.
|
| Előzmény: [2319] Lpont, 2023-12-16 23:55:23 |
|
| [2319] Lpont | 2023-12-16 23:55:23 |
 Nyilván igazad van, hiszen ez a példa a kiegészítéseddel könnyen oldható, de képzeld el, ha így kerül bele egy felvételi feladatsorba. Mennyi időt el lehet vele feleslegesen tölteni és csak körbe-körbe jár mindig azonosságra jutva.
|
| Előzmény: [2318] BerkoErzsebet, 2023-12-16 23:32:59 |
|
| [2318] BerkoErzsebet | 2023-12-16 23:32:59 |
 K Robi írta, hogy példatári feladat. A felvételin remélhetőleg olyan példát adtak, ami néhány perc alatt megoldható. A példatárba valószínű hiányosan, hibásan került bele a példa.
|
| Előzmény: [2317] Lpont, 2023-12-16 23:19:06 |
|
| [2317] Lpont | 2023-12-16 23:19:06 |
 Miből derül ki, hogy Q felezőpont?
Elvárjuk a 14 éves diáktól, hogy javítsa a kitűzést úgy, hogy megoldható legyen a feladat?
Amennyiben az ábra csak "tájékoztató" jellegű, akkor legyen P a QC szakasz tetszőleges belső pontja, de ne illeszkedjen DB-re, minden más feltétel változatlan.
Ekkor, 8<ε<60 esetén végtelen sok megoldás van.
|
| Előzmény: [2316] BerkoErzsebet, 2023-12-16 22:32:57 |
|
| [2316] BerkoErzsebet | 2023-12-16 22:32:57 |
 AB oldalának Q pontja helyett AB oldalának Q felezőpontja
Én is foglalkoztam a példával délután. A stílus nagyon ismerős volt. Sejtettem, hogy felvételi feladat. Azt, hogy az ábra tájékoztató jellegű, mindig odaírják.
|
|
| [2315] Lpont | 2023-12-16 21:45:23 |
 A QCB és a PCB háromszögek hasonlóak, mert mindkettő egyenlő szárú és az alapon fekvő szögeik megegyeznek, ami a C csúcsnál fekvő szög mindkét háromszögben. Ekkor a szárszögek is egyenlőek, tehát CQB szög = PBC szög = ε.
Ha D, P, B pontok kollineárisak, akkor DBC szög = ε és az általad közölt tankönyvi végeredmény szerint a DBC háromszögben a B és C csúcsoknál fekvő szögek összege 16+164=180, vagyis ebben a háromszögben D-nél 0 fok van, a DBC háromszög szakasszá fajul.
|
| Előzmény: [2314] K Robi, 2023-12-16 20:07:42 |
|
| [2314] K Robi | 2023-12-16 20:07:42 |
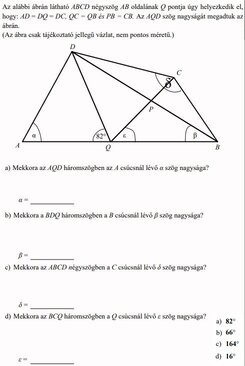
 Köszönöm a választ! "Az ábra csak tájékoztató jellegű vázlat, nem pontos méretű." Lehet, hogy hiba volt ezt lehagynom!
Ez kezd érdekes lenni, képzeld, erre a feladatra egy nyolcadikos felvételi előkészítő példatárban bukkantam, és bevallom, nem ment. Pedig nem nyolcadikos vagyok (nagyon nem), és nem is felvételi körülmények között próbálkoztam vele,és nem is pár percem volt rá, ahogy a nyolcadikus felvételizőknek.
Gyanús, hogy itt valami elírás/nyomdahiba lehet? Persze nekem nagyon tetszene, ha te így is megoldod, csaknem tudom követni, részletezed a megoldásod?
Ideteszem a teljes feladatot kivágva meg a megoldást is a példatár szerint.
|
 |
| Előzmény: [2313] Lpont, 2023-12-16 17:34:37 |
|
| [2313] Lpont | 2023-12-16 17:34:37 |
 Csal az ábra, ha a peremfeltételek igazak, akkor D, P, B nem lehetnek kollineárisak. Némi szögszámolás után P egybeesik Q-val, QCB háromszög szabályos és a kérdőjeles szögek rendre 0, 98, 60.
|
| Előzmény: [2311] K Robi, 2023-12-16 12:04:48 |
|
|
| [2311] K Robi | 2023-12-16 12:04:48 |
 \(\displaystyle AD=DQ=DC\\
QC=QB\\
PB=CB\\\)
Sziasztok! Nyilván \(\displaystyle \alpha=82^{\circ}\) , de hogyan tovább? Nem jövök rá...
\(\displaystyle \beta=?\\
\delta=?\\
\varepsilon=?\)
|
 |
|
| [2310] marcius8 | 2023-12-09 19:27:11 |
 Adott "n" pont egy kör kerületén. Páronként összekötjök a pontokat. Legfeljebb hány részre osztják ezek az összekötő szakaszok a körlemezt. Előre is köszönök minden segítséget.
|
|
|
|
| [2307] sakkmath | 2023-11-08 16:50:39 |
 Az N-nel jelölt konvex, n-oldalú sokszöget háromszögekre bontottuk azon átlóival, amelyek nem metszik egymást N belsejében. Hányféleképpen tehetjük meg ezt?
|
|
| [2306] hanyforint | 2023-08-16 19:11:59 |
 Találtam egy angol nyelvű pdf-et erről, ami több oldalon keresztül elmagyarázza ezt, itt: "https://web.northeastern.edu/seigen/11Magic/StebbinsStack/Si Stebbins Stack - from Numericana dot com.pdf"
|
| Előzmény: [2303] marcius8, 2023-07-19 18:45:26 |
|












