 | English Issue, December 2002 | |||
| Previous page | Contents | Next page | ORDER FORM | |
On János Bolyai's Bicentennial
Elemér Kiss
János Bolyai is one of the greatest figures of Hungarian and universal science. When mentioning his name, one always thinks of his inventive achievements in geometry. This is wholly legitimate, because with the creation of absolute geometry and non-Euclidean geometry in particular, he opened up a new chapter in the history of science. One can rightly assert that few inventions had so great an impact on the development of scientific world-view as that of Bolyai's geometrical invention. His only work published during his lifetime, The Absolutely True Science of Space, was enough to eternally inscribe his name in the history of mathematics. Until recently we used to think that we had a complete knowledge about his life-work. However, the research works of the last decade have shown that concerning the wide problematics of number theory and the question of solubility of algebraic equations Bolyai's works were in the front line of mathematical research, sometimes preceding by decades other great scientists' discoveries.
János Bolyai's 26 pages long work The Absolutely True Science of Space, was issued as an addendum to his father's book entitled Tentamen, therefore, it is often referred to simply as the Appendix. Written in Latin with a remarkable precision and conciseness, it is one of the oustanding achievements in the world history of mathematics and it has been translated into several languages. Bolyai's discovery is not only the first step in the development of modern mathematics, but his ideas had a significant impact on the shaping of natural sciences in general. According to Erik Temple Bell (1883-1960) the developments of hyperbolic geometry revolutionized universal thinking to an even greater degree than the ideas of Copernicus [2]. Bolyai's influence can also be detected in the latest developments of mathematics. It is reflected in his theory of space and in his widespread concepts in modern mathematics.
The Appendix is not the only work János Bolyai left to posterity. Even after the completion of his great work, he studied and took notes continuously. It resulted in his vast legacy of manuscripts, fourteen thousand pages of which are kept in the Teleki-Bolyai Library of Marosvásárhely. These notes contain the ``treasures'' (it was Bolyai's way of naming his newly discovered theorems) that have been brought to light by the research works of recent years.
1. János Bolyai's Course of Life
János Bolyai was born on the 15th of December, 1802 in Kolozsvár [currently Cluj, in Romania]. His father, Farkas Bolyai (1775-1856), became later the erudite professor of the college of Marosvásárhely, whereas his mother, Zsuzsanna Benkő (1782-1821) was the daughter of a surgeon from Kolozsvár.
His later notes and his father's letters provide a detailed account of the first section of his life. He spent his childhood and youth in Domáld [now part of Viisoara-Mures county in Romania] and Marosvásárhely [now Targu-Mures in Romania]. His father gave very careful attention to his son's physical and intellectual education. The nimble, wholesome child showed from the very beginning outstanding intellectual capabilities combined with a sharp perception and an implacable sense of justice. He learned to read and write very easily, as a five years old child he could already distinguish various geometrical figures, he was familiar with the sine function, and recognized the main constellations. He was also unusually talented in learning languages and music. His father imposed on János systematic studying from the age of nine, many subjects were taught to him by his father's more gifted students, but it was his father who taught him mathematics from the very beginning. The extremely talented child shortly became familiar with Euclides's six books, Leonhard Euler's (1707-1783) algebra and even the main part of George Vega's (1754-1802) four-volume handbook.
Farkas Bolyai intended that János continue his studies in Göttingen with his friend of youth, Gauss. He wrote to Gauss in this matter, but his friend did not answer to his letter. Therefore, after due consideration he decided to send his son to the Royal Engineering College of Vienna. In August 1818 János successfully passed the entrance examination and began his career as a soldier.
While staying in Vienna, János was seriously interested in mathematical problems. The seeds of his original ideas are already present in these notes. The illustrations found in his booklet containing solutions to mechanical problems attest to the fact that around the year 1820 he had already began to ponder the unprovability of the axiom of parallelism. In the same year, he experimented with one of the famous, ancient problems, namely, the trisection of angles.
After he had finished his studies, in September 1823 he was appointed second lieutenant to Temesvár (now Timisoara in Romania). It was the place where his more than three years' cogitation, which had started in Vienna, reached a conclusive stage. On a winter night in 1823 he determined the relation holding between the so-called angle of parallels (u) and the distance of parallels (x), which was later written down in S.29 of his Appendix:
| (1) | \(\displaystyle \cot\frac{u}{2}=e^{\frac{x}{k}} \) |
where e=2.718... .
In April 1826 Bolyai was transferred to Arad (now Arad in Romania). In 1831 Bolyai was commanded to go to Lemberg (today Lviv in Ukraine), then in 1832 another order called him to Olmütz (now Olomouc in the Czech Republic). In the previous years he had suffered many times from various diseases, very often from malaria and supposedly also from the infection of the joints. In this period he was especially restless and irritable and he openly manifested his indifference towards military career. The direct consequence of all these was that from the 16th of June 1833 he was sent to retirement.
Meanwhile, János Bolyai's pioneering work, The Absolutely True Science of Space, was published in 1832. This important work [5] was published as an appendix to the first volume of Farkas Bolyai's Tentamen [3], but its off-print had already been ready the previous year, in April 1831 [4]. The latter was the version which, together with a letter, was sent to Gauss by Farkas Bolyai on the 20th of June 1831. Gauss got the letter but János's work was lost on the way. On the 16th of January 1832 Farkas sent the Appendix to his friend again with another letter in which he wrote: ``My son appreciates Your critique more than that of whole Europe and it is the only thing he is waiting for'' [14].
After twenty-three years of silence, Gauss replied to his ``old, unforgettable friend'' on the 6th of March 1832. One of his well-known sentences was: ``if I praised your son's work I would praise myself''. The letter deeply afflicted and upset János Bolyai, although it reflects appreciation, too: ``... I am very glad that it is my old friend's son who so splendidly preceded me'' [14].
After his retirement János Bolyai returned to Marosvásárhely in June 1833. He lived at his father's place for one year, and then he moved to Domáld in 1834. There he lived in seclusion until 1846, when he returned to Marosvásárhely again. His stay at Domáld was not unfruitful in mathematical research either, as former biographers have argued. It was at this time that he wrote his other manuscript, the Responsio, but he was also interested in the solvability of algebraic equations of higher degree and made inquiries into number theory. In the last twenty-seven years of his life he did not publish anything, mainly because of his bad finacial situation, but this does not mean that he was not working.
On the 20th of November 1856 his father died at the age of eighty-one. Farkas Bolyai's death took away from János the only person he could really talk to. From the autumn of 1857 he was ill and confined to bed almost all the time. In January 1860 he got pneumonia and on the 27th he passed away.
Had he lived eight more years, he would have learned that several western mathematicians showed keen interest in his life and significant work. In 1867 the French version [7], and in 1868 the Italian translation [8] of the Appendix are published. At the same time the Grunerts Archiv der Math. und Phys issues the biography of Farkas and János Bolyai [13]. These writings mark the beginning of the vast literature written on the two Bolyais.
2. The Absolutely True Science of Space
Ancient geometry reached its apex in Euclid's work, the Elements. It is a work in which Euclid sets up geometry on the basis of certain fundamental notions and simple assertions called axioms or postulates, while any further concept or theorem is logically deduced from these axioms. Euclid's Postulate V. (in some versions axiom IX.) aroused the interest of mathematicians already in ancient times. Early mathematicians regarded that it was not ``simple'' and ``clear'' enough to satisfy the requirements of an axiom. Thus, they first tried to substitute it with simpler axioms. Later, the idea occured that Postulate V. might not be a fundamental truth at all, just a consequence of other axioms. Proving Postulate V. posed an important question, which concerned for centuries various mathematicians of the world.
János Bolyai was the first to build up a geometry, which neither affirms nor negates Postulate V., but it rather puts it aside: he interpreted parallelism in a way which can intertwine the possibilities of affirming and negating Postulate V. Accordingly, both Euclidean (the \(\displaystyle \Sigma\)-system) and non-Euclidean geometry, or in other words hyperbolic geometry (the S-system) are special cases of the more general geometry Bolyai called absolute geometry. Bolyai's great merit consisted in his invention of absolute geometry and, within it, hyperbolic geometry.
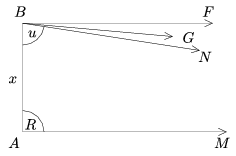
János Bolyai preserves all Euclides's postulates except Postulate V. Just as in common perception, all those basic assumptions which underlie the connecting of points with the help of lines and planes, the transfer of distances and angles with the same extent or the congruence of triangles etc. are also requirements of the S-system. The difference is with regard to the question of parallelism, which Bolyai elucidated in S1. of the Appendix. He defines parallelism not with lines but with half-lines: the directed half-line \(\displaystyle \overrightarrow{BN}\) is parallel with the directed half-line \(\displaystyle \overrightarrow{AM}\) if the counterclockwise rotation of the half-lines from BA around B results in the half-line \(\displaystyle \overrightarrow{BN}\), which does not intersect AM. According to János Bolyai it is clear that from any point B outside line AM there is only one such \(\displaystyle \overrightarrow{BN}\) and that
| (2) | \(\displaystyle \angle\)BAM + \(\displaystyle \angle\)ABN \(\displaystyle \le\)2R |
(R refers to the right angle).
Parallelism defined in such a way is called absolute parallelism, and if in case (2) we only allow the use of sign < then we talk about hyperbolic parallelism. In the latter case there are two - oppositely directed - parallels to AM through point B. In the hyperbolic definition there are several half-lines \(\displaystyle \overrightarrow{BG}\) which are neither parallel with \(\displaystyle \overrightarrow{AM}\) nor do they intersect it. Thus, while on the Euclidean plane two distinct lines either intersect or are parallel to each other, on the hyperbilic plane there are lines which neither intersect nor are they parallels.
Both in its content and in its form János Bolyai's Appendix is one of the basic works in the history of mathemetics. Absolute geometry widely and deeply influenced further investigations. It opened up the way for new developments, which, in turn, extended their scope beyond mathematics, influencing physics and other related sciences. However, its immediate influence was on the development of mathematics.
The birth of Bolyai's geometry is a turning point in the history of the axiomatic method. His work put an end to all those axiomatic investigations, which - for thousands of years - had attempted to tackle the problem of parallelism. At the same time, these investigations opened up the way for a whole row of modern inquiries connected with the axiomatic method. The questions of independence and compatibility of the axiomatic systems rose for the first time in a close relation to non-Euclidean geometry.
Finally, I would like to emphasize that the invention of absolute geometry is solely János Bolyai's merit. He was the first to think of its creation, which was not done with the help of non-Euclidean geometry. For him, non-Euclidean geometry was a kind of gift resulting from absolute geometry.
3. Number Theory
All Bolyai-monographs unanimously assert: although János Bolyai tried his hand at a few problems in number theory, his investigations were not particularly successful. However, his manuscripts attest the opposite of all this. Bolyai had a keen interest in questions of number theory and he had several original ideas, with which he preceded many other mathematicians of later ages.
Among the very first theorems found in Bolyai's legacy is the following: If p and q are prime numbers, and a is an integer divisible neither by p nor by q, and if ap-1\(\displaystyle \equiv\)1 (mod q) and aq-1 \(\displaystyle \equiv\)1 (mod p), then
| (3) | apq-1 \(\displaystyle \equiv\)1 (mod pq) |
[11].
We can readily observe that it is the same theorem which James Hopwood Jeans (1877-1946) published decades later in 1898. Since we can definitely affirm that this relation was first recognized and demonstrated by János Bolyai, I propose that in the future it should be called Bolyai-Jeans Theorem.
At a time János Bolyai thought that he could find the formula of prime numbers by means of Fermat's little theorem. This is why he tried to prove its converse. As a result, he reached conclusion (3). By substituting a=2 in this relation, with repeated attempts he got the numbers p=11, q=31, and thus Bolyai found the smallest pseudoprime number with respect to 2, that is, 341, for which
2340 \(\displaystyle \equiv\)1 (mod 341).
Thus, he showed that the converse of the so-called ``little theorem'' of Pierre de Fermat (1601-1665) was not true. We can remark that the only one who found the number 341 in Bolyai's time was an anonymous scientist [1], but Bolyai was not aware of this.
Bolyai's further observations concerning the Fermat's little theorem can be found in [11].
János Bolyai's inquiries concerning Fermat's two-square theorem are very valuable. The theorem goes as follows: every prime of the form 4k + 1 (\(\displaystyle k\in\mathbb{N}\)) can be written as a sum of two squares. The theorem had been formulated by Fermat but it was demonstrated by Leonhard Euler (1707-1783) at about one hundred years later. Euler's proof reached the Teleki Téka of Marosvásárhely, where Farkas Bolyai read it. The proof seemed too long and complicated to him. Therefore, he asked his son to provide him with the ``simplest'' demonstration of the theorem. Within a short period of time János sent his father a two-page letter with four possible solutions to the problem. His solutions were so simple, because he deployed his achievements regarding the question of complex integers. One of his solutions is especially simple [12]. We feel, that nobody has provided a more brilliant solution to this theorem than Bolyai.
In addition to these theorems János Bolyai dealt with several other number theoretical problems too, namely, with the Pell equation. Since he did not know that the converse of the Wilson's theorem - if (n-1)! \(\displaystyle \equiv\)- 1 (mod n), then n is prime - had already been demonstrated by Lagrange, he, just as his father, sought a solution to this problem. In his own words: ``both my father and I solved the converse of the so beautiful and important Wilson's theorem'' [6].
We mention, that one can find in his manuscripts even a magic square:
|
János Bolyai constructs his magic square in a general way, using letters.
Bolyai got the bulk of his knowledge concerning number theory from Gauss's Disquisitiones Arithmeticae (1801). Including the most important and most recent problems, Gauss had sent a copy of his Disquisitiones, dedicated to his friend, Farkas Bolyai (Amico suo de Bolyai per curam Pauli Vada, auctor) as early as 1803. János could have read it in his early childhood, because at the age of 13 he already spoke Latin. But later, he definitely bought some of Gauss's work in Vienna. The latter copy, accompanied by Bolyai's glosses can be found in the Library of the Hungarian Academy of Sciences. Farkas Bolyai's book is in the Teleki-Bolyai Library of Marosvásárhely.
We used to think [15] that Hungarian mathematics did not have significant achievements in number theory up to the last quarter of the 19th century. If we take into consideration János Bolyai's ideas mentioned above, then it turns out that the first investigations in number theory started half a century earlier. Indeed, János Bolyai was the first to do such inquiries in Hungary. We can assert that the first Hungarian mathematician to produce significant achievements in the field of number theory was János Bolyai.
4. Algebraic Investigations
János Bolyai was also greatly interested in the solvability of algebraic equations. We can infer from his notes that for a long time he had tried in vain to prove the solubility of the equation of fifth degree, but later, realizing his error, also he got to the Ruffini-Abel theorem. He found the problem in the works of Gauss, Andreas von Ettingshausen (1796-1887), Joseph Luis Lagrange (1736-1813) and Farkas Bolyai. He often mentions in his notes Ettinghausen's work published [9] in 1827 in Vienna, in which the author mentions Paolo Ruffini's (1765-1822) ``demonstration'' of the solvability of algebraic eqations higher than fourth degree, dating from 1799. Bolyai was quick to realize the flaw of Ruffini's paper. His manuscripts attest to the fact that he successfully corrected Ruffini's mistake and proved that such equations cannot be solved. He asserts: ``the general equation of fifth degree is unsolvable ... the easiest correct way is Ruffini's `solution' modified by myself'' [6]. However, before Bolyai put down his ideas in this topic, mathematicians had already been familiar with Niels Abel's (1802-1829) flawless demonstration from 1826. Bolyai did not know about either Abel's or his contemporary's, Evariste Galois's (1811-1832) works. The history of mathematics, in its turn, did not know that in the middle of the 19th century there was a Hungarian mathematician, who solved one of the most important algebraic problems.
5. Conclusions
There are very few scientists whose work is appreciated in their lifetime. The inventors of non-Euclidean geometry did not have the opportunity to enjoy the triumph of their discovery. Above all, János Bolyai would have deserved much better recognition. His demonstration that the Euclidean axiom of parallelism was independent of other axioms brought an end to a period of development of two millennia. He solved one of the most lasting problems of geometry and thus created the concept of modern geometry. At the same time, he also obtained significant results in other branches of mathematics.
Now, on the occasion of his bicentennial it is necessary to evoke his course of life, his ideas and his mathematical activity in the light of the most recent examinations. Thus, we can get a more detailed and colourful portrait of the great inventor of geometry.
Acknowledgments. I thank the Domus Hungarica Scientarium et Artium and Arany János Közalapítvány for their support, which made the writing of this paper possible.
References
[1] Anonymus, Théorémes et problémes sur les nombres, Journal für die reine und angewandte Mathematik, 6 (1830), 100-106.
[2] Erik Temple Bell, The Development of Mathematics, Dover Publication, INC. New York (is an unabridged and unaltered publication of the second edition, 1945).
[3] Farkas Bolyai, Tentamen juventutem studiosam in elementa puraem, ... Timus I-II, Marosvásárhely, 1832-33.
[4] János Bolyai, Appendix prima scientia spatti ..., Marosvásárhely, 1831 április.
[5] János Bolyai, Appendix. Scientiam spatii absolute veram ..., Marosvásárhely, 1832. (Attached to Farkas Bolyai's Tentamen).
[6] János Bolyai's manuscripts, Targu-Mures: Teleki-Bolyai Library.
[7] Jeans Bolyai, La science absolute de l'espace ..., Traduit par Guillame-Jules Hoüel, Memoires de la Société des sciences physiques et naturelles de Bordeaux, V. Bordeaux, 1867.
[8] Giovanni Bolyai, Sulla scienza dello spazio assolutamente vera ..., Versione dal latino per Giuseppe Battaglini, Giornale di Matematica, 6 (1868), Napoli, 97-116.
[9] Andreas von Ettingshausen, Vorlesungen über die höhere Mathematik, Wien, 1827.
[10] Elemér Kiss, Mathematical Gems from the Bolyai Chests, Budapest: Akadémiai Kiadó, 1999.
[11] Elemér Kiss, Notes on János Bolyai's Researches in Number Theory, Historia Mathematica 26, (1999), 68-76.
[12] Elemér Kiss, A Short Proof of Fermat's Two-Square Theorem Given by János Bolyai, Mathematica Pannonica, 8 (2) (1997), 293-295.
[13] Franz Schmidt, Aus dem Leben zweier ungarischer Mathematiker, Johann und Wolfgang Bolyai von Bolya, Grunerts Archiv der Math. und Phys., 48 (1868), 217-228.
[14] Franz Schmidt and Paul Stäckel, Briefwechsel zwischen Carl Friderich Gauss und Wolfgang Bolyai, Leipzig: Teubner, 1899.
[15] Barna Szénássy, History of Mathematics in Hungary until the 20th Century, Springer-Verlag, Berlin Heidelberg New York London Paris Tokyo Hong Kong Barcelona Budapest, 1992.
