Solutions for problems "A" in September, 2000
In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.
A. 242. 2001 points are given in a 5x5x10 rectangular box. Prove that there can be found two points among them whose distance is less than 0.7.
Solution. Put a sphere of radius 0.35 around each point. The sum of
volumes of the spheres is  . Offsetting the
faces of the box by 0.35, the augmented box contains all the spheres. The
volume of this augmented box is 5.7x5.7x10.7
. Offsetting the
faces of the box by 0.35, the augmented box contains all the spheres. The
volume of this augmented box is 5.7x5.7x10.7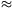 347.6 which is smaller than the sum of volumes of all spheres.
Thus, the interiors of the spheres are cannot be pairwise disjoint. But, if two
spheres have a common interior point, their centers are closer than 0.7.
347.6 which is smaller than the sum of volumes of all spheres.
Thus, the interiors of the spheres are cannot be pairwise disjoint. But, if two
spheres have a common interior point, their centers are closer than 0.7.
A. 243. Determine all pairs of prime numbers p,q which satisfy
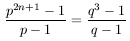 for some integer
n>1.
for some integer
n>1.
Proposed by: E. Fried, Budapest
Solution. Subtracting 1 and multiplying by (p-1) we obtain
p(pn-1)(pn+1)=(p-1)q(q+1).
If q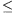 pn-1 then the factors on the left hand side are
greater than the factors on the right hand side, respectively; thus q
pn-1 then the factors on the left hand side are
greater than the factors on the right hand side, respectively; thus q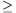 pn. Because q is a prime but pn is not, this implies q
pn. Because q is a prime but pn is not, this implies q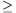 pn+1.
pn+1.
One of the factors of the left hand side is divisible by the prime q. By the last inequality, this is possible only if q=pn+1. Substituting this,
p(pn-1)=(p-1)(pn+2), thus pn-3p+2=0.
Then p|2, p=2, n=2, finally q=pn+1=5.
A. 244. A sequence of numbers is called of Fibonacci-type if each term, after the first two, is the sum of the previous two. Prove that the set of positive integers can be partitioned into the disjoint union of infinite Fibonacci-type sequences.
Proposed by: B. Énekes, Tolna
Solution 1. We define a funcion f: N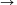 N; this function will map from any positive integer to the next
element of the corresponding Fibonacci-type sequence.
N; this function will map from any positive integer to the next
element of the corresponding Fibonacci-type sequence.
Let f(1)=2. If f(1), ..., f(n-1) are already defined, then check whether n is one of the defined values of the function. If n=f(m) for some m, then take the smallest such m and let f(n)=n+m. If n is not a value, then let f(n)=f(n-1)+1.
The first values of this function are:
| f(1)=2 | |
| f(2)=2+1=3 | because 2=f(1) |
| f(3)=3+2=5 | because 3=f(2) |
| f(4)=5+1=6 | |
| f(5)=5+3=8 | because 5=f(3) |
| f(6)=6+4=10 | because 6=f(4) |
| f(7)=10+1=11 | |
| f(8)=8+5=13 | because 8=f(5) |
| f(9)=13+1=14 | |
| f(10)=10+6=16 | because 10=f(6) |
| f(11)=11+7=18 | because 11=f(7) |
| ... |
For each positive integer n, which is not a value of f, take the sequence n, f(n), f(f(n)), ... . These sequences are Fibonacci-type, because by the definition of f, for all x, f(f(x))=f(x)+x .
1 2
2 3
3 5
5 8
8 13
13 ...
...
4 6
6 10
10 16
16 26
26 42
42 ...
...
7 11
11 18
18 29
29 47
47 76
76 ...
...
9 14
14 23
23 37
37 60
60 ...
...
...
First we prove that for all n f(n)>n. By
induction, if n=f(m), then
f(n)=n+m>n. If n f(m) for any m, then
f(n)=f(n-1)+1>(n-1)+1=n.
f(m) for any m, then
f(n)=f(n-1)+1>(n-1)+1=n.
Now we prove that f is strictly increasing. This has been seen for
n<10. If n f(m) for
any m, then
f(n)=f(n-1)+1>f(n-1). If
n=f(m), then by the previous result m<n,
and only one such m can exist. Let k=f(m-1); of
course k<n. The numbers k+1, k+2, ..., n-1
are between the values f(m-1)=k and
f(m)=n . Thus
f(m) for
any m, then
f(n)=f(n-1)+1>f(n-1). If
n=f(m), then by the previous result m<n,
and only one such m can exist. Let k=f(m-1); of
course k<n. The numbers k+1, k+2, ..., n-1
are between the values f(m-1)=k and
f(m)=n . Thus
| f(k)=k+(m-1) | because k=f(m-1), |
| f(k+1)=f(k)+1=k+m, | |
| f(k+2)=f(k+1)+1=k+m+1, | |
| ... | |
| f(n-1)=f(n-2)+1=n+m-2. | |
| f(n)=n+m, | because n=f(m). |
Also in this case we have f(n)>f(n-1).
By these properties the sequences cover all the positive integers and they are pairwise disjoint.
Solution 2. Similarly to the previous solution, we define a function
f: N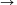 N
which is strictly increasing and satisfies
f(f(n))=f(n)+n.
N
which is strictly increasing and satisfies
f(f(n))=f(n)+n.
Let 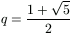 , the positive root of the equation
q2=q+1. For an arbitrary positive integer n let
f(n) be the closest integer to qn.
, the positive root of the equation
q2=q+1. For an arbitrary positive integer n let
f(n) be the closest integer to qn.
The function is strictly increasing, because the difference between qn and q(n+1) is q>1, thus the closest integer to q(n+1) is greater than the closest integer to qn.
Finally, for all n we have
|f(f(n))-f(n)-n|=|f(f(n))-qf(n)+(q-1)f(n)-q(q-1)n|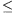
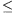 |f(f(n))-qf(n)|+(q-1)|f(n)-qn|
|f(f(n))-qf(n)|+(q-1)|f(n)-qn|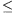
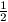 +(q-1).
+(q-1).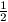 <1,
<1,
thus f(f(n))-f(n)-n=0.
Solution 3 (by A. Zsbán and P. Csívári). It is well-known, that any positive integer can uniformly be written as the sum of different Fibonacci numbers such that no neighboring Fibonacci numbers are used, for example, 17=1+3+13. Consider a positive integer, for which the Fibonacci number 1 is one of the terms. Shifting in such a way that each term is replaced by the next element of the Fibonacci sequence, another number is obtained, repeating this step we obtain a Fibonacci-type sequence:
1+3+13 2+5+21
2+5+21 3+8+34
3+8+34 5+13+55
5+13+55 ...
...
Doing this construction for any possible number, we obtain infinitely many Fibonacci-type sequences. Each positive integer n is contained by a single sequence, because the first element of the corresponding sequence can be determined by shifting back the terms of n; for example, the number 100=3+8+89 is contained by the sequence beginning with 1+2+34=37.
1, 2, 3, 5, 8, 13, 21, ...
4=1+3, 7=2+5, 11=3+8, 18=5+13, 29=8+21, ...
6=1+5, 10=2+8, 16=3+13, 26=5+21, 42=8+34, ...
9=1+8, 15=2+13, 24=3+21, 39=5+34, 63=8+55, ...
12=1+3+8, 20=2+5+13, 32=3+8+21, 52=5+13+34, ...
...
