Solutions for exercises "C" in September, 2000
In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.
C. 590. According to the law of gravity, an object falling
free to the earth's surface moves through s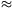 4.903t2 meters in t
seconds. How is this formula modified if distance is measured in feet and time
is measured in minutes?
4.903t2 meters in t
seconds. How is this formula modified if distance is measured in feet and time
is measured in minutes?
Solution. One feet is approximately 0.305 meter. Thus
s feet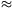 0,305s meter, and
t minutes=60t seconds. Substituting these to the
formula,
0,305s meter, and
t minutes=60t seconds. Substituting these to the
formula,
0,305s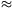 4,903.(60t)2,
4,903.(60t)2,
s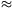 57900t2.
57900t2.
C. 591. Ann thought of 5 numbers and told Bob the list of all the sums that can be obtained by adding any two of the numbers. This list goes as follows: 6,7,8,8,9,9,10,10,11,12. Help Bob to find out which numbers Ann was thinking of.
Solution. Denote the five numbers by a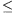 b
b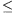 c
c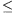 d
d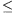 e.
e.
The two smallest sums are a+b and a+c; the two largest ones are c+e and d+e. Thus we know that
(1) a+b=6;
(2) a+c=7;
(3) c+e=11;
(4) d+e=12;
Another equation can be obtained for example by summing all the sums of two numbers. Each one of the five numbers is added 4 times, thus the sum of all two-term sums is 4(a+b+c+d+e):
4(a+b+c+d+e)=6+7+8+8+9+9+10+10+11+12=90,
(5) a+b+c+d+e=22.5.
From equations (1)-(5) the five numbers can be computed easily: a=2.5, b=3.5, c=4.5, d=5.5 and e=6.5. Finally we have to check that really 2,5+3.5=6, 2,5+4.5=7, 2,5+5.5=8, 3,5+4.5=8, 2,5+6.5=9, 3,5+4.5=9, 3,5+6.5=10, 4,5+5.5=10, 4,5+6.5=11 and 5,5+6.5=12.
C. 592. Determine the average of all 5-digit palindromes. (A palindrome like 12421 is a number, reading the same backward as forward.)
Solution. A 5-digit palindrom is determined by its first three digits. The first digit can be 1,2,...,9, the other ones can be 0,1,...,9. The number of the palindroms is 9.10.10=900.
Each of the digits 1,2,...9 stays 100 times at the 1st and the 5th position, and each of 0,1,...,9 stays 90 times at the 2nd, 3rd and 4th position. So, the sum of all palindroms is (1+...+9).(10000+1).100+(1+...+9).(1000+10).90+(1+...+9).100.90. The average of the palindroms is 45.(1000100+90900+9000)/900=55000.
C. 593. Peter selected a few stamps from his collection; one of each of the face values: 1,2,...,37 forints. His plan is to arrange them in groups such that the sum of the face values is the same in each group. How many different arrangements can be made?
C.593. 1+2+...+37=37.38/2=19.37=703. 19 and 37 are prime, so the number of the groups can be 1,19,37 or 703. The sum of values in a group is at least 37, because there is a 37 forint stamp. Thus there is a single group, or there is 19 groups and the sum of values is 37 in each group.
If there is 19 groups, then the 37-forint stamp forms a group in itself. Each of the other 18 groups must contain at least two stamps to add 37. On the other hand, the number of the remaining stamps is 2.18. Thus each these 18 groups contain exactly two stamps, and the groups are 37, 36+1, 35+2, 34+3, ..., 19+18.
There exist two possible grouping.
C. 594. In a cyclic trapezium, a and d denote the length of one base and the sum of the lengths of the other three sides. Given a and d, determine the sides of the trapezium which has a maximal area.
Solution. The trapezium can exist only if d>a. Denote x the length of the sides of the trapezium; then the length of the other base is d-2x (0<x<d/2).
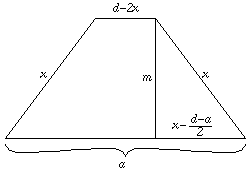
By Pythaogras' theorem, the height of the trapezium is
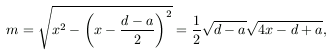
and the area is
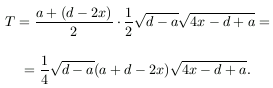
We have to find the maximum of  . The
first derivative of f is
. The
first derivative of f is
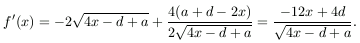
If 0<x<d/3 then f'(x)>0, thus f is increasing.
If d/3<x<d/2 then f'(x)<0, thus f(x) is decreasing. The maximum is at x=d/3.
