Solutions for problems "A" in October, 2000
In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.
A. 245. We want to make a round trip with our car. There are a few gas-stations along the road where the total amount of fuel is enough to make two round trips. Prove that there is a station from where the round trip can be completed in both directions.
Solution. The proof works by induction with respect to the number of gas-stations.
If each station contains enough fuel to reach the two neighbouring ones, the
problem is trivial. So assume the there exist two neighbouring stations at the
points A and B of the trip such that the gas-station at A
does not contain enough fuel to reach B. Denote the amount of fuel at
the two gas-stations by a and b. It can be assumed that a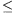 b, otherwise A and B can be
exchanged.
b, otherwise A and B can be
exchanged.

Denote by C the point between A and B, which can be reached if we start from A. Now we modify the configuration of the trip and the gas-stations. Reduce the amount of fuel at A and B to 0 and b-a, respectively; moreover, decrease the length of arc AB by the distance AC. In this modified configuratioon the total amount of fuel is enough to make two round trips again, but the empty gas-station at A can be removed. Thus, by the induction, there exists a gas-station S from where the round trip is possible in both directions. We show that starting from this station, the round trips are possible in the original case as well.
Start a trip from S. While A and B are not reached, there is no difference between the original and the modified situation. Reaching A or B, there is two differences between the two configurations: first, in the original case, the next part of the trip is longer by the distance AC; second, we can take the extra amount a of fuel, which is exactly enough to pass this extra distance. Thus we can pass the arc AB. After leaving A and B we always have more fuel in the original case than in the modified configuration.
A. 246. Find all quadruples of real numbers x, y, z, w which satisfy x+y+z+w=x7+y7+z7+w7=0.
Shay Gueron, Haifa
Solution.
Lemma. If a,b are real numbers and a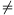 0, then the system X+Y=a,
X7+Y7=b of equations has at most one solution (ignoring
the order of variables).
0, then the system X+Y=a,
X7+Y7=b of equations has at most one solution (ignoring
the order of variables).
Proof. Let X=a/2-Z,
Y=a/2+Z. By the simmetry it can be assumed that Z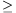 0. Substituting this into the second equation,
0. Substituting this into the second equation,
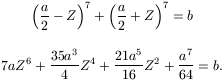
The left hand side is strictly increasing or decreasing in Z if a>0 or a<0, respectively. Thus the equation holds for at most one Z. The lemma is complete.
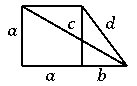
Now we prove that all solutions for system (1) contain of two pairs of
complement real numbers. Suppose that the sum of two of the variables is not
zero, say x+y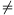 0. Let
a=-(x+y) and b=-(x7+y7). The numbers
z,w satisfy the system
0. Let
a=-(x+y) and b=-(x7+y7). The numbers
z,w satisfy the system
z+w=a, z7+w7=b.
The pair (-x,-y) is a solution for this system; by the lemma there is no more solution. Thus z=-x and w=-y, or z=-y and w=-x
If the sum of any two of x,y,z,w is 0, then x=y=z=w=0.
A. 247. Prove that there is no point on the lines determined by the sides of the unit square whose distance from each vertex of the square is rational.
Á. Kovács, Budapest
Solution. We will use several times the following two lemmas.
lemma 1. Suppose that the positivce integers A, B and C are relative prime and satisfy A2+B2=C2.
a) If A is even, then there exist some relative prime positive integersP and Q such that A=2PQ, B=P2-Q2 and C=P2+Q2;
b) If A is odd, then there exist some relative prime positive odd integers P and Q such that A=PQ, B=(P2-Q2)/2 and C=(P2+Q2)/2.
Proof. From the equation A2=(B+C)(B-C). In case a), the greatest common divisor of the two factor is 2; then there exist some positive integers P, Q such that B+C=2P2 and B-C=2Q2. This implies the statement.
In case b), the two factors are relative prime, thus they are odd squares; B+C=P2 and B-C=Q2 for some odd P and Q. This also imples the statement.
lemma 2. If A,B,C,D are positive integers and AB=CD, then there exist some positive integers P,Q,R,S such that A=PQ, B=RS, C=PR and D=QS. If the pairs A,B and C,D are relative prime, respectively, then P,Q,R,S are pairwise relative prime.
Proof. Let P=(A,C), Q=A/P, R=C/P and S=B/R=D/Q. (The last equation holds, because B/R=BP/C=ABP/AC=CDP/AC=DP/A=D/Q.) These numbers satisfy the equation; we only have to show that S is integral.
By the construction, Q and R are relative prime; thus Qx+Ry=1 for some integers x and y. Then S=(Qx+Ry)S=(QS)x+(RS)y=Dx+By is integral.
The second part of the lemma follows from the fact that the numbers A=PQ, B=RS, and C=PR, D=QS are relative prime, respectively.
lemma 3. if there exists a point on a line determined by a side of the unit square, then the system
(1a) x2+y2=zw; (1b) z2-w2=2xy
has positive integral solution.
Proof. The point cannot be a vertex of the cube. Magnify the square and the point such that the side of the suqre and the four distances are all integers.
By Pythagoras' theorem
a2+(a+b)2=c2; a2+b2=d2.
Choose the scaling such that a and b are relative prime. By the first equation, one of a and a+b must be even, the other one is odd. This implies that b is odd. From the second condition, a is even.
By lemma 1 there exist some positive integers p,q,r,s such that p and q, r and s are relative prime, respectively, and
a=2pq, a+b=p2-q2, c=p2+q2
and
a=2rs, b=r2-s2, d=r2+s2.
(We obtain the same if the point is an interior point of the edge of the square.)
Solving the equations for a,
(2) p2-q2-r2+s2=2pq=2rs.
By lemma 2, pq=rs implies that there exist some positive integers x,y,z,w which are pairwise relative prime and satisfy p=xz, q=yw, r=xw and s=yz. Substitute these into (2):
x2z2-y2w2-x2w2+y2z2=2xyzw;
(3) (x2+y2)(z2-w2)=2xy.zw.
There can be at most one even number between x,y,z,w. If all of them are odd, then the left-hand side of (3) is divisible by 4, the right-hand side not; this is a contradiction. Thus, one of x,y,z,w is even. Then the right-hand side of (3) is divisible by 4; on the leftt-hand side the factor x2+y2 is not divisible by 4, thus z2-w2 is even. This implies that z and w are odd; so one of x and y must be the even one. The factor x2+y2 is odd.
The number x2+y2 is relative prime to 2xy, because it is relative prime to x and y, moreover it is odd. The number z2-w2 is relative prime to zw. So, (3) can hold only if x2+y2=zw and z2-w2=2xy, in other words, the quadruple (x,y,z,w) i s a solution for the system (1a), (1b).
4. lemma. The system (1a),(1b) has no positive integer solution.
Proof. Suppose that there exist solutions, and take a solution for which the product xyzw is minimal.
If both x and y are divisible by a prime number p, then, by (1a), z or w is divisible by p as well; by (1b) this implies that both z and w is divisible by p. In this case a smaller solution can be obtained dividing all variables by p. Thus, x and y must be relative prime. In a similar way we can prove that also z and w are relative prime.
The number z2-w2=2xy is even; this is possible only if z and w are odd. Then x2+y2=zw is odd, so one of x and y is even. By the symmetry it can be assumed that x is even and y is odd.
Equation (1b) says  , moreover we know
that the pairs (z+w)/2, (z-w)/2 and x/2,
y are relative prime. By lemma 2 there exist some positive integers
k,l,m,n which are pairwise relative prime and
, moreover we know
that the pairs (z+w)/2, (z-w)/2 and x/2,
y are relative prime. By lemma 2 there exist some positive integers
k,l,m,n which are pairwise relative prime and
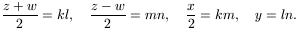
From this x=2km, y=ln, z=kl+mn and w=kl-mn. Substitute these quantities into (1a):
4k2m2+l2n2=k2l2-m2n2;
(4) 5k2m2=(k2-n2)(l2+m2).
On the right-hand side, the factor k2-n2 is relative prime to k2, and l2+m2 is relative prime to m2. Thus (4) can hold only in two cases:
Case 1: k2-n2=m2 and l2+m2=5k2;
case 2: k2-n2=5m2 and l2+m2=k2.
In case 1,
(5a) k2-n2=m2, (5b) l2+m2=5k2.
The number y=ln is odd, n is even. From equation (5a),
k is odd and m is even. By lemma 1 and (5a), there exist some odd
positive integers  and
and  such that
such that
n=
 m=(
m=( 2-
2- 2)/2, k=(
2)/2, k=( 2+
2+ 2)/2.
2)/2.
Substituting this to (5b),
( 2+
2+ 2)2+(
2)2+(
 )2=l2.
)2=l2.
Again, by lemma 1 there exist some positive integers 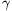 and
and 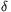 such that
such that
 2+
2+ 2=2
2=2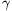
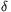 ,
, 
 =
=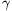 2-
2- 2, l=
2, l=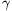 2+
2+ 2.
2.
TThus, the quartet ( ,
,  ,
, 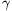 ,
, 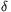 ) is a solution for the system (1); but, at the
same time,
) is a solution for the system (1); but, at the
same time,
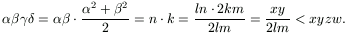
This contradicts the minimality of the quartet (x,y,z,w).
In case 2,
(6a) k2-n2=5m2, (6b) l2+m2=k2.
Similarly to the previous case, l is odd; by equation (6b), m
is even and k is odd. By lemma 1 and equation (6b), there exist some odd
positive integers  and
and  such that
such that
l=
 , m=(
, m=( 2-
2- 2)/2, k=(
2)/2, k=( 2+
2+ 2)/2.
2)/2.
Substitute these in (6a):
( 2-
2- 2)2+n2=(
2)2+n2=(
 )2.
)2.
Again, by lemma 1 there exist some positive integers 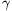 ,
, 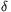 such that
such that
 2-
2- 2=2
2=2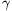
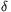 , n=
, n=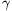 2-
2-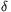 2,
2, 
 =
=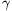 2+
2+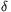 2.
2.
In this case the quartet (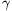 ,
,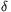 ,
, ,
, ) is a solution for the system (1a),(1b),
contradicting
) is a solution for the system (1a),(1b),
contradicting