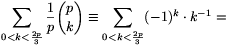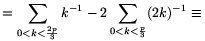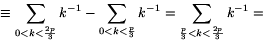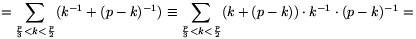Solutions for problems "A" in September, 2001

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

A. 269. A round hole is to be completely covered with two square boards. The sides of the squares are 1 metre. In what interval may the diameter of the hole vary?

Solution. It is easy to see that a hole of radius $\displaystyle 2-\sqrt2$ (and all smaller holes) can be covered by two unit squares, see Figure 1.

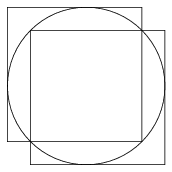
Figure 1

We will prove that if a unit square covers at least half of the perimeter of a circle of radius r, then $\displaystyle r\le2-\sqrt2$. This implies that the diameter of the hole cannot exceed $\displaystyle 4-2\sqrt2\approx1.17$ metre.

Let K be a circle of radius r, and N be a unit square, which covers at least the half of K. If r$\displaystyle ge$1/2, then N can be translated such that each side of N or its extension has at least one common point with K and the covered part of the curve is increasing, see Figure 2.

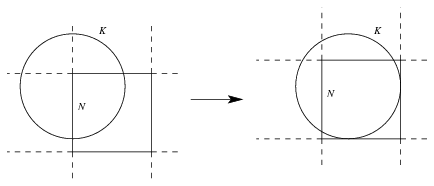
Figure 2

So, it can be assumed that r>1/2 and (the extension of) each side of N has a common point with K.

First, consider the case when a vertex of N is inside K. Let the vertices of N be A, B, C, D and suppose that A is inside K. Denote the intersecion of K and the half-lines AB and AD by P and Q, respectively. (Figure 3.)

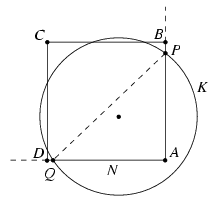
Figure 3

Because PAQ$\displaystyle angle$=90^o, the centre of K and vertex A are on the same side of line PQ. This implies that the uncovered arc PQ is longer than the half of K. This is a contradiction, thus this case is impossible.

We are left to deal the case when there are no vertices of N inside K and each side or its extension has a common point with K. It is easy to check that these common points cannot be on the extension of the sides of N; they must lie on the perimeter of N.

Denote by $\displaystyle alpha$, $\displaystyle beta$, $\displaystyle gamma$ and $\displaystyle delta$ the angles drawn in Figure 4.

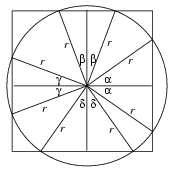
Figure 4

The total of the uncovered arcs is at most the half of K, so $\displaystyle alpha$+$\displaystyle beta$+$\displaystyle gamma$+$\displaystyle delta$ $le$ 90^o. By symmetry, it can be assumed that $alpha$ + $gamma$ $le$ 45^o.

As can be read from the Figure, r(cos $alpha$ +cos $gamma$ )=r(cos $beta$ +cos $delta$ )=1. The concavity of the cosine function yields

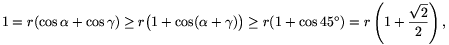
$1=r(\cos\alpha+\cos\gamma)\ge r\big(1+\cos(\alpha+\gamma)\big)\ge r(1+\cos45^\circ)=r\left(1+{\sqrt2\over2}\right),$

and hence 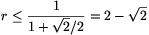$r\le{1\over1+\sqrt2/2}=2-\sqrt2$ .

Thus, the radius of the hole can be at most 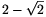$2-\sqrt2$ ; its diameter can be at most 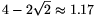$4-2\sqrt2\approx1.17$ metre.

A. 270. Prove that if a, b, c, d are positive numbers then

(1)	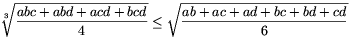$\root3\of{abc+abd+acd+bcd\over4}\le\sqrt{ab+ac+ad+bc+bd+cd\over6}$

Solution 1. Define the folowing symmetric expressions of a, b, c, d:

S₃₃=a³b³+a³c³+a³d³+b³c³+b³d³+c³d³;

S₃₂₁=a³b²c+a³b²d+...+bc²d³;

S₃₁₁₁=a³bcd+ab³cd+abc³d+abcd³;

S₂₂₂=a²b²c²+a²b²d²+a²c²d²+b²c²d²;

S₂₂₁₁=a²b²cd+a²bc²d+a²bcd²+ab²c²d+ab²cd²+abc²d².

Taking the 6th power of (1), we obtain

(2)	2S₃₃+6S₃₂₁+12S₃₁₁₁ $ge$ 15S₂₂₂+24S₂₂₁₁.

By the A.M.-G.M. inequality

2S₃₃=(a³b³+a³c³+b³c³)+(a³b³+a³d³+b³d³)+

+(a³c³+a³d³+c³d³)+(b³c³+b³d³+c³d³) $ge$

$ge$ 3a²b²c²+3a²b²d²+3a²c²d²+3b²c²d²=3S₂₂₂.

We similarly obtain that S₃₂₁ $ge$ 6S₂₂₂, S₃₂₁ $ge$ 4S₂₂₁₁ and 3S₃₁₁₁ $ge$ 2S₂₂₁₁. Thus

2S₃₃+6S₃₂₁+12S₃₁₁₁=2S₃₃+2^.S₃₂₁+4^.S₃₂₁+4^.3S₃₁₁₁ $ge$

$ge$ 3S₂₂₂+2^.6S₂₂₂+4^.4S₂₂₁₁+4^.2S₂₂₁₁=15S₂₂₂+24S₂₂₁₁.

Solution 2. The polynomial f(x)=(x-a)(x-b)(x-c)(x-d) has four positive (not necessariliy different) roots. Thus, its derivative has three positive roots; denote them by u, v and w.

By Viete's formulae,

f'(x)=4x³-3(a+b+c+d)x²+

+2(ab+ac+ad+bc+bd+cd)x-(abc+abd+acd+bcd)=

=4(x³-(u+v+w)x²+(uv+uw+vw)x-uvw).

Thus

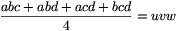
${abc+abd+acd+bcd\over4}=uvw$

and

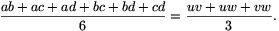
${ab+ac+ad+bc+bd+cd\over6}={uv+uw+vw\over3}.$

Substituting these in (1), it becomes the inequality between the arithmetic and geometric means of uv, uw and vw.

A. 271. Prove that for any prime, p $ge$ 5, the number

(1)	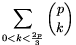$\sum_{0<k<{2p\over3}}{p\choose k}$

is divisible by p².

Vojtech Jarnik Mathematics Competition, Ostrava, 2001

Solution. Each term of (1) is divisible by p, so our goal is to prove that

(2)	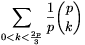$\sum_{0<k<{2p\over3}}{1\over p}{p\choose k}$

is divisible by p.

For an arbitrary integer 1 $le$ x<p, let x^-1 be the multiplicative inverse of x modulo p.

For all 0<k<p,

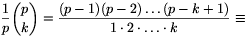
${1\over p}{p\choose k}={(p-1)(p-2)\dots(p-k+1)\over1\cdot2\cdot\dots\cdot k}\equiv$

$equiv$ (-1)^.(-2)^....^.(-k+1)^.1^-1^.2^-1^....^.k^-1 $equiv$ (-1)^k^.k^-1 (mod p),

and

$\sum_{0<k<{2p\over3}}{1\over p}{p\choose k}\equiv\sum_{0<k<{2p\over3}}(-1)^k\cdot k^{-1}=$

$=\sum_{0<k<{2p\over3}}k^{-1}-2\sum_{0<k<{p\over3}}(2k)^{-1}\equiv$

$\equiv\sum_{0<k<{2p\over3}}k^{-1}-\sum_{0<k<{p\over3}}{k}^{-1}=\sum_{{p\over3}<k<{2p\over3}}k^{-1}=$

$=\sum_{{p\over3}<k<{p\over2}}(k^{-1}+(p-k)^{-1})\equiv\sum_{{p\over3}<k<{p\over2}}(k+(p-k))\cdot k^{-1}\cdot(p-k)^{-1}=$

$=\sum_{{p\over3}<k<{p\over2}}p\cdot k^{-1}\cdot(p-k)^{-1})\equiv0\pmod p.$

Already signed up?
New to KöMaL?