Exercises and problems in Physics
September 2001

Please read The Conditions of the Problem Solving Competition.

Experimental problem

M. 226.  Use a drawing board to make a slope with a variable angle. Fit the bottom of the drawing board to the edge of the table so that a sliding body could leave the slope without collision and fall freely on the floor. Take measurements to find out what sloping angle a coin sliding from the top of the drawing board falls furthest. Does the result depend on the length of the drawing board, on the height of the table or on the coin itself?

Theoretical problems It is allowed to send solutions for any number of problems, but final scores of students of grade 9-12 are computed from the 5 best score in each month. Final scores of students of grade 1-8 are computed from the 3 best scores in each month.

P. 3445.  Julie and Steve live in the same street, Julie in a 300 m and Steve in a 800 m distance from the school. In the morning they leave for school at the same time. Steve goes by bike at a speed of 10 m/s and Julie goes on foot at a speed of 2 m/s. When they meet, Steve gets off his bike and they walk on together talking to each other at a speed of 1 m/s. Will they reach the school before the school bell rings if they started from home 3 minutes before the ring? (3 points)

P. 3446.  There is a force of 800 N exerted on a man standing in a lift due to gravitation. The force exerted on the lift by the man (his weight) is 820 N. At what rate does the lift accelerate and in which direction? What can we say of the velocity of the lift? (3 points)

P. 3447.  Let's fill an air-balloon to the same volume once with hydrogen and once with helium. In which case is the lifting capacity greater and by what percentage? (In the given conditions the gas densities in kg/m³ units are: hydrogen -- 0.08, helium -- 0.16, air -- 1.162). The mass of the balloon's material is negligible compared to the mass of the burden and the volume of the burden is negligible compared to the volume of the balloon. (3 points)

P. 3448.  Let's push up a crate of a mass of 10 kg slowly on a slope. The work needed to achieve this is 400 J. By pulling the same crate down the slope we use work of 250 J. (The force of both pushing and pulling is parallel to the direction of the slope.) What is the height of the slope? (4 points)

P. 3449.  There are three elastic disks with masses m₁=m₃=0.15 kg, m₂=0.2 kg connected with two equal length strings of negligible mass, on a horizontal air-cushioned table. At the beginning the three disks are in rest and reside in one line (according to the figure). Then we make the middle disk move horizontally and perpendicular to the strings with a velocity of v₀=6 m/s.

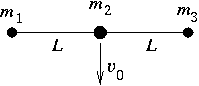
a) What is the velocity of the side disks right at the moment when the disk of mass m₂ stops after the elastic collision of the two disks in question? What is the angle formed by the two strings in this position?

b) What is the angle formed by the two strings in this position? (6 points)

P. 3450.  There is a ship sailing east along the Equator with a speed of 45 km/h. How much time does a pendulum-clock on board lose in 3 hours if it keeps good time when the ship rests relative to the Earth. (5 points)

P. 3451.  A solid piece of metal with a volume of 50 cm³ and a temperature of 20 ^oC can be lifted to a height of 100 m by using 135 J of work. What would be the temperature of the same object if we transmitted to it an amount of heat equivalent to the work used in lifting. (4 points)

P. 3452.  The measuring limit of a standard voltage meter with the resistance of R=1 k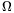 can be extended to 60 V, 150 V and 300 V as can be seen in the figure. The sum of the three additional resistances is 9 k\(\displaystyle Omega\). What are the separate resistance values, and how much is the measuring limit of the basic instrument U₀? (4 points)

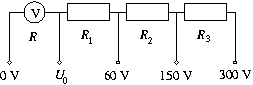
P. 3453.  A semicylinder made of a transparent plastic has a refraction index of n=1.41 and a radius of R=5 cm. There is a narrow incident laser beam perpendicular to the flat side of the semicylinder at d distance from the axis of symmetry.

a) What can the maximum value of d be so that the laser beam can still leave the other side of the semicylinder?

b) How can the refraction index be determined if we know d_max and R?

c) By varying distance d, in which interval will distance OB shown in the figure vary? (4 points)

P. 3454.  In 1923 George Hevesy determined the age of a rock sample with some uranium content based on the finding that the ratio of the number of ²³⁸U atoms to the number of ²⁰⁶Pb atoms present in the sample was 3:2. What was the age he determined? (4 points)

P. 3455.  The Sun emits electromagnetic radiation with the power of 3.86x10²⁶ W.

a) How much energy arrives per second at the top of the Earth's atmosphere on a 1 m² surface perpendicular to the radiation coming from the Sun?

b) How much is the impulse of the light incident on a surface of 1 m² in one second?

c) What is the pressure exerted by the incoming light on a surface that is perpendicular to the radiation and absorbs every kind of light? (4 points)

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary

solutions@komal.elte.hu.

Deadline: 11 October 2001