New exercises and problems in Mathematics
September 2001

Please read The Conditions of the Problem Solving Competition.

New exercises in September 2001

Maximum score for each exercise (sign "C") is 5 points.

C. 635. In an arithmetic class, pupils are asked how many legs a hen, six dogs and seven palpigradis have in total. (``Palpigradi'' is the Latin name of a certain animal). Alex says 46, Ben says 52, Cecilia says 66, Dora says 78, and Edith says 82. Who is right?

Based on a problem of a Zrínyi Competition

C. 636. In the Cartesian coordinate system, represent the set of points whose coordinates x and y satisfy -2$\displaystyle le$x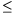2, -3$\displaystyle le$y$\displaystyle le$3, {x}$\displaystyle le${y} ({z} denotes the difference between the number z and the greatest integer less than or equal to z.)

C. 637. Find the positive integer that has two digits both in base 10 and in base 8, and for which the sum of the digits is fourteen in both number systems.

C. 638. How many different square prisms are possible in which the lengths of the edges in cm are integers and the measure of the surface area in cm² equals the measure of the volume in cm³?

C. 639. How many pairs (a;b) of positive integers are there with 1$\displaystyle le$a$\displaystyle le$2001, 1$\displaystyle le$b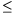2001, where the lowest common multiple of a and b is 2001?

New problems in September 2001

The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3472. How many time instants are there between 6 a.m. and 6 p.m. when it is not possible to tell the time if we cannot distinguish the long and short hands of the clock? (3 points)

Kvant

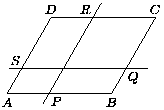
B. 3473. The area of parallelogram ABCD is 2 units. The line parallel to AD intersects the boundary of the parallelogram at P and R, and the line parallel to AB intersects it at S and Q, as shown in the figure. What is the total area of the triangles AQR, BSR, DPQ and CSP? (3 points)

B. 3474. What is the seventy-third digit from the back in the number $\displaystyle (\underbrace{111\dots1}_{112})^2$? (4 points)

B. 3475. The angles of a triangle with sides a, b, c are $\displaystyle alpha$, $\displaystyle beta$, $\displaystyle gamma$. Prove that if 3$\displaystyle alpha$+2$\displaystyle beta$=180^o, then a²+bc-c²=0. (4 points)

International Hungarian Mathematics Competition, 2001

B. 3476. An interior point of a regular decagon is connected to each vertex to form 10 triangles. The triangles are coloured red and blue alternately. Prove that the total blue area equals the total red area. (4 points)

B. 3477. What is the maximum possible value of the sine of 2ⁿ degrees if n is a positive integer? (4 points)

B. 3478. The centres of the exscribed circles of triangle ABC are O₁, O₂, O₃. Prove that the area of triangle O₁O₂O₃ is at least four times the area of triangle ABC. (4 points)

Proposed by: Á. Besenyei, Budapest

B. 3479. Find the minimum value of the expression 6t²+3s²-4st-8t+6s+5. (4 points)

B. 3480. Given are the points A, B, C and D in this order on the line e. What is the locus of those points P in the plane for which the angles APB and CPD are equal? (5 points)

Gillis--Turán Mathematics Competition

B. 3481. Let $\displaystyle f_1(x)=-{{2x+7}\over{x+3}}$, f_n+1(x)=f₁(f_n(x)). Evaluate f₂₀₀₁(2002). (4 points)

New advanced problems in September 2001

Maximum score for each advanced problem (sign "A") is 5 points.

A. 269. A round hole is to be completely covered with two square boards. The sides of the squares are 1 metre. In what interval may the diameter of the hole vary?

A. 270. Prove that if a, b, c, d are positive numbers then 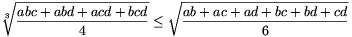$\root3\of{abc+abd+acd+bcd\over4}\leq\sqrt{ab+ac+ad+bc+bd+cd\over6}$ .

A. 271. Prove that for any prime, p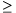5, the number 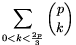$\sum_{0<k<{2p\over3}}{p\choose k}$ is divisible by p².

Vojtech Jarnik Mathematics Competition, Ostrava, 2001

Send your solutions to the following address:

or by e-mail to:

solutions@komal.elte.hu

Already signed up?
New to KöMaL?