 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
Sz. 1. We learned from an article of József Bölcsföldi and Géza Balázs (KöMaL Homepage Dec. 2000) that ``already the Pythagoreans knew about numbers that form a friendly pair--which is a pair (a,b) of natural numbers with both numbers being equal to the sum of the proper divisors (i.e. including 1 but excluding the number itself) of the other. Clearly, one number in a friendly pair has many divisors (typed in bold below), while the other one has only few of them. Some friendly pairs include (220, 284), (1184, 1210), (2620, 2924), (5020, 5564), (6232, 6368), (10744, 10856), ...'' Write a program which asks for two natural numbers (N<M<106), then prints all the friendly pairs (a,b) with N<a, b<M. (10 points)
Sz. 2. In most programming languages an ellipse can be displayed by a single command, however this ellipse must have axes parallel to the edges of the screen. Write a program that enables us to draw the ellipse in any position. The parameters are the length of the axes and the angle between the major axis and the upper edge of the screen in degrees. (10 points)
Sz. 3. We deposit our savings for N years (1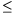
N\(\displaystyle le\)10) according to the following:
1. Throughout N years, at the beginning of every month we place
A Forints into the bank, and lock it up for one year at a rate
of interest X percent (X>0 a real number). 2. When
the lockup is over, at the beginning of the next month we get the
yearly interest, which is put back and locked up again for one year
together with our savings so far. Make a sheet (named PENZ.XLS) which
the numbers N, A and X can be entered into, then
our bank balance is calculated throughout N years. The sheet
should contain exactly N rows, that is unnecessary rows should
not be visible even if N is changed. Example (with N=3,
A=1000, X=10)
|
(10 points)