Solutions for exercises "C" in October, 2001

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

C. 640. In the Gregorian calendar, there are 97 leaping days on 29 February during the course of 400 consecutive years. In how many years will the difference between the Gregorian calendar and the ``true'' calendar amount to 1 day if the exact length of the solar year is 365 days 5 hours 48 minutes and 46 seconds?

Solution. The Gregorian calendar offers 97 leap days (that is, 97^.24=2328 hours) per 400 years, as opposed to 400 times the 5 hours, 48 minutes and 46 seconds. 48 minutes make 4/5 of an hour, and thus 5 and 4/5 hours per year add up to 2320 hours per 400 years, which is 8 hours less than 97 days. The Gregorian calendar gains 8 hours, i.e. 28,800 seconds against the 400^.46=18400 seconds. The difference is 10400 seconds per 400 years. It takes (400^.86400)/10400$\displaystyle sim$3323 years for this difference to add up to a whole day (i.e. 86,400 seconds).

C. 641. A rectangular sheet of paper is folded along its diagonal. The parts sticking out over the edge of the overlapping area are cut off, and the sheet is unfolded. Now it has the shape of a rhombus. The rhombus is then folded along a line through the midpoints of two opposite sides, and the overhanging pieces are cut off again. What should the original rectangle be like so that the result is a regular hexagon?

Solution.

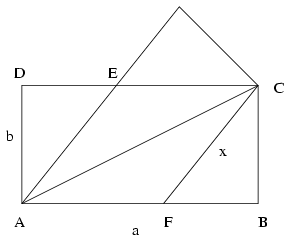
In the rectangle ABCD, AB=a, AD=b, and let x denote the side of the rhombus.

In the right-angled triangle ADE, x²=b²+(a-x)², hence

(1): $\displaystyle x={a^2+b^2\over2a}$

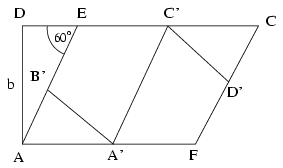
By folding the rhombus along a midline, we get the regular hexagon A'B'EC'D'F. C'EB'$\displaystyle angle$=120^o, thus in the right-angled triangle ADE, AED$\displaystyle angle$=60^o, and from $\displaystyle {b\over x}=\sin60^{\circ}$, $\displaystyle x={2\sqrt3\over3}b$. (2)

It follows from (1) and (2) that

$\displaystyle {2\sqrt3\over3}b={a^2+b^2\over2a}.$

By rearranging and solving the equation, we get $\displaystyle a=\sqrt3b$. This gives the ratio of the sides of the rectangle. It is easy to see that the hexagon is regular.

C. 642. Find all the natural numbers with the following property: If the last two digits of the square of the number are interchanged, the result is the square of the next natural number.

Proposed by: E. Fried, Budapest

Solution. If the last two digits of n² are A and B (in this order) then the last two digits of (n+1)² are B followed by A. Hence

2n+1=(n+1)²-n²=(10B+A)-(10A+B)=9(B-A).

It immediately follows that B-A is odd. A=0 is impossible, as in a square number ending in 0 the last but one digit is also 0, which makes B=0, but 2n+1 cannot be 0. Therefore B>A. Considering that B$\displaystyle le$9, we have B-A$\displaystyle le$9-1=8. As B-A is odd, B-A$\displaystyle in${1,3,5,7}. Hence n$\displaystyle in${4,13,22,31}. The squares of the corresponding pairs are 16 and 25; 169 and 196; 484 and 529; 961 and 1024. The requirement is only satisfied by one of them: 13.

C. 643. The area of triangle ABC is t, its perimeter is k, the radius of the circumscribed circle is R. Prove that $\displaystyle 4tR\leq\left({k\over3}\right)^3$.

Solution.

Using the conventional notation for the sides and angles of the triangle ABC, we have $\displaystyle t={ab\sin\gamma\over2}$, $\displaystyle R={c\over2\sin\gamma}$ and k=a+b+c. By substituting into the inequality, it can be simplified to $\displaystyle abc\leq\left({a+b+c\over3}\right)^3$. This is obviously true, as a, b, c are positive, and their arithmetic mean is greater than or equal to their geometric mean. Equality only occurs in the case of the equilateral triangle.

C. 644. The angles of a triangle are , és . Prove that $\displaystyle {{\cos\alpha}\over{\sin\beta\sin\gamma}}+{{\cos\beta}\over{\sin\alpha\sin\gamma}}+{{\cos\gamma}\over{\sin\alpha\sin\beta}}=2$.

Proposed by: J. L. Díaz, Barcelona

Solution. The identity to be proved is

$\displaystyle {\cos\alpha\over\sin\beta\sin\gamma}+{\cos\beta\over\sin\alpha\sin\gamma}+{\cos\gamma\over\sin\alpha\sin\beta}=2.$

By multiplication by the non-zero 2sin$\displaystyle alpha$sin$\displaystyle beta$sin$\displaystyle gamma$, and applying the identity for the sine of the double angle to $\displaystyle alpha$ and $\displaystyle beta$, we get that sin2$\displaystyle alpha$+sin2$\displaystyle beta$+2sin$\displaystyle gamma$cos$\displaystyle gamma$=4sin$\displaystyle alpha$sin$\displaystyle beta$sin$\displaystyle gamma$.(1)

The sum of the first two terms on the left-hand side is sin2$\displaystyle alpha$+sin2$\displaystyle beta$=2sin($\displaystyle alpha$+$\displaystyle beta$)cos($\displaystyle alpha$-$\displaystyle beta$).

As $\displaystyle alpha$+$\displaystyle beta$+$\displaystyle gamma$=180^o, on the left-hand side of (1) we have 2sin$\displaystyle gamma$(cos($\displaystyle alpha$-$\displaystyle beta$)+cos$\displaystyle gamma$)=2sin$\displaystyle gamma$(cos($\displaystyle alpha$-$\displaystyle beta$)-cos($\displaystyle alpha$+$\displaystyle beta$))(2)

For the sum in the brackets, we obtain

cos($\displaystyle alpha$-$\displaystyle beta$)-cos($\displaystyle alpha$+$\displaystyle beta$)=-2sin$\displaystyle alpha$sin(-$\displaystyle beta$)=2sin$\displaystyle alpha$sin$\displaystyle beta$ thus (2) does equal the right-hand side of (1).