New exercises and problems in Mathematics
October 2001

Please read The Conditions of the Problem Solving Competition.

New exercises in October 2001

Maximum score for each exercise (sign "C") is 5 points.

C. 640. In the Gregorian calendar, there are 97 leaping days on 29 February during the course of 400 consecutive years. In how many years will the difference between the Gregorian calendar and the ``true'' calendar amount to 1 day if the exact length of the solar year is 365 days 5 hours 48 minutes and 46 seconds?

C. 641. A rectangular sheet of paper is folded along its diagonal. The parts sticking out over the edge of the overlapping area are cut off, and the sheet is unfolded. Now it has the shape of a rhombus. The rhombus is then folded along a line through the midpoints of two opposite sides, and the overhanging pieces are cut off again. What should the original rectangle be like so that the result is a regular hexagon?

C. 642. Find all the natural numbers with the following property: If the last two digits of the square of the number are interchanged, the result is the square of the next natural number.

Proposed by: E. Fried, Budapest

C. 643. The area of triangle ABC is t, its perimeter is k, the radius of the circumscribed circle is R. Prove that $\displaystyle 4tR\leq\left({k\over3}\right)^3$.

C. 644. The angles of a triangle are $alpha$ , $beta$ és $gamma$ . Prove that $\displaystyle {{\cos\alpha}\over{\sin\beta\sin\gamma}}+{{\cos\beta}\over{\sin\alpha\sin\gamma}}+{{\cos\gamma}\over{\sin\alpha\sin\beta}}=2$.

Proposed by: J. L. Díaz, Barcelona

New problems in October 2001

The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3482. Four good friends notice that if each of them divides the number of the books he has by the sum of the digits of that number, they all get the same integer: 13. Prove that at least two of them have the same number of books. (4 points)

Proposed by: L. Gerőcs, Budapest

B. 3483. The midpoint of side AB of a rectangle ABCD is F. P is a point on the angle bisector from C. The orthogonal projection of P on the line BC is Q. Prove that if line PF is perpendicular to line DQ then AP=BC. (3 points)

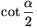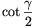B. 3484. The angles of a triangle are $alpha$ , $beta$ , $gamma$ . $\cot{{\alpha}\over2}$ , $\displaystyle \cot{{\beta}\over2}$, $\cot{{\gamma}\over2}$ are consecutive integers. Find the largest angle of the triangle. (3 points)

B. 3485. The elements of the set A are positive integers. If x, y$\displaystyle in$A, x>y then 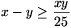$x-y\geq{{xy}\over{25}}$ . How many elements can the set A have at most? (4 points)

Vojtech Jarnik mathematics competition, Ostrava, 2001

B. 3486. Given 2001 points and a circle of unit radius in the plane, prove that there exists a point on the circumference of the circle such that the sum of its distances from the given points is at least 2001. (4 points)

International Hungarian Mathematics Competition, 2001

B. 3487. f(x) is a function defined on positive real numbers, and f(x)+2^.f(1/x)=3x+6 everywhere in the domain. Find all such functions f(x). (3 points)

B. 3488. The lengths of the sides of a rectangular billiards table ABCD are AB=150 cm and BC=205 cm. There are four holes, one in each corner. At corner A, a ball is struck in a direction enclosing an angle of 45^o with the side of the table, and it is moving away from the hole. Whenever the ball hits the edge of the table, it rebounds elastically. What will happen to the ball? (4 points)

B. 3489. Prove that 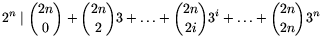$2^n\mid{2n\choose0}+{2n\choose2}3+\dots+{2n\choose2i}3^i+\dots+{2n\choose2n}3^n$ . (5 points)

B. 3490. The benches of the Great Hall of the Parliament of Neverenough are arranged in a rectangle of 10 rows of 10 seats each. All the 100 MPs have different salaries. Each of them asks all his neighbours (sitting next to, in front of, or behind him, as well as those four seated diagonally in front of or behind him, i.e. 8 members at most) how much they earn. They feel a lot of envy towards each other: an MP is content with his salary only if he has at most one neighbour who earns more than himself. What is the maximum possible number of MPs who are satisfied with their salaries? (4 points)

Kvant

B. 3491. Is the following statement true or false? ``Given n red points in the space, it is always possible to place 3n blue points in the space such that there is at least one blue point in the interior of each tetrahedron determined by the red points.'' (5 points)

from the idea of Z. Füredi

New advanced problems in October 2001

Maximum score for each advanced problem (sign "A") is 5 points.

A. 272. The benches of the Great Hall of the Parliament of Neverenough are arranged in a rectangle of 10 rows of 10 seats each. All the 100 MPs have different salaries. Each of them asks all his neighbours (sitting next to, in front of, or behind him, i.e. 4 members at most) how much they earn. They feel a lot of envy towards each other: an MP is content with his salary only if he has at most one neighbour who earns more than himself. What is the maximum possible number of MPs who are satisfied with their salaries?

Adapted from Kvant

A. 273. The inscribed circle of triangle ABC touches the sides AB, BC, CA at the points C₁, A₁, B₁ respectively. Given vertex A, line A₁B₁, and the line joining the midpoint of segment B₁C₁ to vertex B, construct the triangle ABC with ruler and compasses.

Proposed by: T. Kálmán, Budapest

A. 274. Let a, b, c be positive integers for which ac=b²+b+1. Prove that the equation ax²-(2b+1)xy+cy²=1 has an integer solution.

Polish competition problem

Send your solutions to the following address:

or by e-mail to:

solutions@komal.elte.hu

Already signed up?
New to KöMaL?