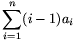|
Solutions for advanced problems "A" in November, 2001 |
In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.
A. 275. The numbers 12, 22, 32, ..., (n2)2 are written in increasing order into an nxn array:
|
A number is selected from each row, such that no two numbers belong to the same column. What are the possible values of the sum of the selected numbers?
From the idea of T. Terpai
Solution. Suppose we have chosen the aith element out of the i-th row, where i=1,2,...,n. The numbers a1,...,an represent a permutation of 1,2,...,n, and the sum of the selected numbers is
\(\displaystyle \sum_{i=1}^n\big((i-1)n+a_i\big)^2=n^2\sum_{i=1}^n(i-1)^2+\sum_{i=1}^na_i^2+2n\sum_{i=1}^n(i-1)a_i.\)
The values of the first two sums do not depend on the choice of the numbers ai:
\(\displaystyle n^2\sum_{i=1}^n(i-1)^2=n^2\cdot{(n-1)n(2n-1)\over6}={n^3(n-1)(2n-1)\over6},\)
\(\displaystyle \sum_{i=1}^na_i^2=\sum_{i=1}^ni^2={n(n+1)(2n+1)\over6}.\)
According to the ordering theorem, the third sum is minimum if the numbers ai form a decreasing sequence, and maximum if they form an increasing sequence. Thus the lowest and highest values are
\(\displaystyle 2n\sum_{i=1}^n(i-1)(n-i+1)=2n\cdot{(n-1)n(n+1)\over6},\)
and
\(\displaystyle 2n\sum_{i=1}^n(i-1)i=2n\cdot{(n-1)n(n+1)\over3}.\)
It is easy to check with a little calculation that for small values of n, the possible values of \(\displaystyle \sum_{i=1}^n(i-1)a_i\) are as follows:
|
For all n\(\displaystyle ge\)5, \(\displaystyle \sum_{i=1}^n(i-1)a_i\) assumes every integer value between \(\displaystyle {(n-1)n(n+1)\over6}\) and \(\displaystyle {(n-1)n(n+1)\over3}\). The proof is by induction. As shown above, the statement is true for n=4.
If the statement is true for some n=m, then in the case n=m+1, consider the sequences a1,...,am+1, such that am+1=m+1 or a1=m+1.
If am+1=m+1 then
\(\displaystyle \sum{i=1}^n(i-1)a_i=\sum_{i=1}^ma_i+(m-1)m,\)
and we get the same sums as in the case n=m, but incremented by m(m+1). These sums are, therefore, the integers between \(\displaystyle A={(m-1)m(m+1)\over6}+m(m+1)\) and \(\displaystyle B={(m-1)m(m+1)\over3}+m(m+1)={m(m+1)(m+2)\over3}\).
If a1=m+1, then
\(\displaystyle \sum_{i=1}^n(i-1)a_i=\sum_{i=2}^{m+1}(i-1)a_i=\sum_{i=1}^mia_{i+1}=\)
\(\displaystyle =\sum_{i=1}^m(i-1)a_{i+1}+\sum_{i=1}^na_{i+1}=\sum_{i=1}^m(i-1)a_{i+1}+{m(m+1)\over2},\)
thus here we get the same sums again, but this time incremented by \(\displaystyle {m(m+1)\over2}\). The resulting sums are, therefore, the integers between \(\displaystyle C={(m-1)m(m+1)\over6}+{m(m+1)\over2}={m(m+1)(m+2)\over6}\) and \(\displaystyle D={(m-1)m(m+1)\over3}+{m(m+1)\over2}\).
It is easy to check that if m\(\displaystyle ge\)4 then C<A\(\displaystyle le\)D<B, and thus all integers between C and B are represented. This completes the proof.
Answer: For n\(\displaystyle ne\)3, the possible values of the sum of the elements selected from the table are in arithmetic progression, where the lowest member is
\(\displaystyle {n^3(n-1)(2n-1)\over6}+{n(n+1)(2n+1)\over6}+2n\cdot{(n-1)n(n+1)\over6}={n(2n^4-n^3+3n^2+n+1)\over6},\)
the largest member is
\(\displaystyle {n^3(n-1)(2n-1)\over6}+{n(n+1)(2n+1)\over6}+2n\cdot{(n-1)n(n+1)\over3}={n(2n^4+n^3+3n^2-n+1)\over6},\)
and the common difference is 2n.
Fof n=3, the result is similar, but with the middle term of the sequence, 95 missing; the possible values are 83, 89, 101 and 107.
A. 276. The product of the positive numbers
x1, ..., xn is 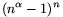 ,
where
,
where 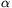
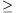 1 is a real
number. Prove that
1 is a real
number. Prove that
\(\displaystyle \sum_{i=1}^n{1\over(x_i+1)^{1/\alpha}}\ge1.\)
Solution. Let \(\displaystyle f(t)={1\over(t+1)^{1/\alpha}}\). We shall prove the following two lemmas:
Lemma 1. If a\(\displaystyle le\)b\(\displaystyle le\)c\(\displaystyle le\)d are positive numbers, and ad=bc, then
f(a)+f(d)\(\displaystyle ge\)min(f(b)+f(c),1).
Lemma 2. If the geometric mean of the numbers x1,x2,...,xn is m, then
f(x1)+f(x2)+...+f(xn)\(\displaystyle ge\)min(n.f(m),1).
The statement of the problem is a special case of lemma 2, because if the product of the positive numbers x1,...,xn is (n\(\displaystyle alpha\)-1)n, i.e. their geometric mean is m=n\(\displaystyle alpha\)-1, then n.f(m)=1.
Proof for lemma 1. Let \(\displaystyle m=\sqrt{ad}=\sqrt{bc}\), and
\(\displaystyle g(t)=f(mt)+f(m/t)=\bigg(mt+1\bigg)^{-{1\over\alpha}}+\bigg({m\over t}+1\bigg)^{-{1\over\alpha}}\)
for all positive t, and t1=c/m, t2=d/m. Then 1\(\displaystyle le\)t1\(\displaystyle le\)t2, and the statement is that
g(t2)\(\displaystyle ge\)min(g(t1),1).
It follows from the definition that \(\displaystyle \lim\limits_\infty g=1.\)
Let us examine the monotonicity of the function g on the interval [1,\(\displaystyle infty\)). The derivative of the function g is
\(\displaystyle g'(t)={m\over\alpha}\left(-\bigg(mt+1\bigg)^{-{\alpha+1\over\alpha}}+{1\over t^2}\bigg({m\over t}+1\bigg)^{-{\alpha+1\over\alpha}}\right),\)
which is positive if and only if
\(\displaystyle \bigg(mt+1\bigg)^{\alpha+1\over\alpha\)t^2\bigg({m\over t}+1\bigg)^{\alpha+1\over\alpha}.">
By raising to the \(\displaystyle {\alpha\over\alpha+1}\)th power and rearranging, we have
\(\displaystyle t^{2\alpha\over\alpha+1}-mt+mt^{\alpha-1\over\alpha+1}-1<0.\)
Let h(t) denote the left-hand side. For further investigation, we will need the first two derivatives of the function h, and the values of h(1) and h'(1):
\(\displaystyle h(t)=t^{2\alpha\over\alpha+1}-mt+mt^{\alpha-1\over\alpha+1}-1,\qquad h(1)=0;\)
\(\displaystyle h'(t)={2\alpha\over\alpha+1}t^{\alpha-1\over\alpha+1}-m+{\alpha-1\over\alpha+1}mt^{-{2\over\alpha+1}},\qquad h'(1)={2\over\alpha+1}(\alpha-m);\)
\(\displaystyle h''(t)={2\alpha(\alpha-1)\over(\alpha+1)^2}t^{-{\alpha+3\over\alpha+1}}\bigg(t-{m\over\alpha}\bigg).\)
Now let us distinguish the following cases, depending on the values of m and \(\displaystyle alpha\):
Case 1. : \(\displaystyle alpha\)=1 and m\(\displaystyle le\)1.
Case 2. : \(\displaystyle alpha\)=1 and m>1.
Case 3. : \(\displaystyle alpha\)>1 and m\(\displaystyle le\)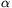 .
.
Case 4. : 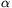 >1 and m>
>1 and m>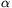 .
.
In case 1, h(t)=(1-m)(t-1)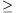 0 for all t>1, thus h
0 for all t>1, thus h 0 in the interval (1,
0 in the interval (1, ).
).
In case 2, h(t)=(1-m)(t-1)<0 for all t>1, thus h<0 in the interval (1, ).
).
In case 3, h''>0 for h'(1) 0 and t>1, thus h'>0 in the entire interval (1,
0 and t>1, thus h'>0 in the entire interval (1, ). As h(1)=0, it follows that h>0 in the interval (1,
). As h(1)=0, it follows that h>0 in the interval (1, ).
).
In case 4, h'(1)<0, and h''<0 in the interval (1,m/ ). Thus h'<0 in that interval. As h(1)=0, it follows that h<0 in the interval (1,m/
). Thus h'<0 in that interval. As h(1)=0, it follows that h<0 in the interval (1,m/ ]. In the interval (m/
]. In the interval (m/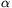 ,
,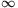 ), h''>0, that is, the function h is convex down. As h(m/
), h''>0, that is, the function h is convex down. As h(m/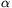 )<0 and
)<0 and 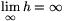 , it follows that there exists a real number
, it follows that there exists a real number 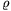 >1, such that h<0 on the interval (1,
>1, such that h<0 on the interval (1,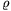 ), and h>0 on the interval (
), and h>0 on the interval (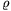 ,
,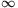 ).
).
In either case, if h(t2)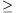 0, then h
0, then h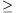 0 in the entire interval (t2,
0 in the entire interval (t2,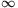 ), that is, g'
), that is, g' 0. Hence the function g monotonically decreases in the interval [t2,
0. Hence the function g monotonically decreases in the interval [t2,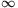 ), and
), and 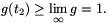 If h(t2)
If h(t2) 0, then h
0, then h 0 in the interval (1,t2), that is, g'
0 in the interval (1,t2), that is, g'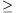 0. Thus g imonotonically increases, and és g(t1)
0. Thus g imonotonically increases, and és g(t1) g(t2). Lemma 1 is proved.
g(t2). Lemma 1 is proved.
Proof for lemma 2. The proof is by induction. If n=1 then only x1=m is possible, and the statement is meaningless. Assume that n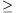 2, and the statement is true if the number of variables is less than that.
2, and the statement is true if the number of variables is less than that.
The sequence x1,...,xn contains both a number not greater than m, and a number not smaller than m. We can suppose, for example, that x1 m
m x2. Let y1 denote the smaller number out of m and x1x2/m, and let y2 denote the larger number. Then x1
x2. Let y1 denote the smaller number out of m and x1x2/m, and let y2 denote the larger number. Then x1 y1
y1 y2
y2 x2 and y1y2=x1x2. With lemma 1, it follows that
x2 and y1y2=x1x2. With lemma 1, it follows that
| (2) | f(x1)+f(x2)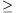 min(f(y1)+f(y2),1)=min(f(m)+f(y2),1). min(f(y1)+f(y2),1)=min(f(m)+f(y2),1). |
The geometric mean of the numbers y2,x3,...,xn is also m. The assumption can be applied, and we get
| (3) | f(y2)+f(x3)+...+f(xn)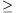 min((n-1)f(m),1). min((n-1)f(m),1). |
If f(x1)+f(x2)>1, then f(x1)+...+f(xn)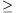 f(x1)+f(x2)>1, and hence the statement is true. If f(x1)+f(x2)
f(x1)+f(x2)>1, and hence the statement is true. If f(x1)+f(x2) 1, then (2) states that f(x1)+f(x2)
1, then (2) states that f(x1)+f(x2)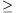 f(m)+f(y2). Using this result, and (3), we have
f(m)+f(y2). Using this result, and (3), we have
f(x1)+f(x2)...+f(xn)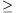 f(m)+f(y2)+f(x3)+...+f(xn)
f(m)+f(y2)+f(x3)+...+f(xn)
 f(m)+min((n-1)f(m),1)=min(nf(m),f(m)+1)
f(m)+min((n-1)f(m),1)=min(nf(m),f(m)+1) min(nf(m),1).
min(nf(m),1).
Thus lemma 2 is proved, and so is the statement of the problem
A. 277. Let H1 be an n-sided polygon. Construct the sequence H1, H2, ..., Hn of polygons as follows. Having constructed the polygon Hk, Hk+1 is obtained by reflecting each vertex of Hk through its k-th neighbour in the counterclockwise direction. Prove that if n is a prime, then the polygons H1 and Hn are similar.
Solution 1. In order to be able to formulate auxiliary statements more accurately, the following solution uses arrays of n points rather than n-sided polygons.
For every integer 0<k<n, let  k denote the transformation that maps an array of n points onto another by reflecting each point in its kth successor. The definition of the transformation can be extended to any integer k if k is considered modulo n.
k denote the transformation that maps an array of n points onto another by reflecting each point in its kth successor. The definition of the transformation can be extended to any integer k if k is considered modulo n.
The statement is that Hk+1= k(Hk), and we need to prove that the n-gon
k(Hk), and we need to prove that the n-gon  n-1(
n-1( n-2(...
n-2(... 2(
2( 1(H1))...)) is similar to H1.
1(H1))...)) is similar to H1.
First we shall prove that the transformations commute, that is, for all integers k,m and every array P of n numbers,  m(
m( k(P))=
k(P))= k(
k( m(P)). Let the points of P be p1, ..., pn. Then, with all the indices taken modulo n,
m(P)). Let the points of P be p1, ..., pn. Then, with all the indices taken modulo n,
- the ith point of the polygon  k(P) is 2pi+k-pi;
k(P) is 2pi+k-pi;
- the ith point of the polygon  m(P) is 2pi+m-pi;
m(P) is 2pi+m-pi;
- the ith point of the polygon  m(
m( k(P)) is 2(2pi+m+k-pi+m)-(2pi+k-pi)=4pi+m+k-2pi+k-2pi+m+pi;
k(P)) is 2(2pi+m+k-pi+m)-(2pi+k-pi)=4pi+m+k-2pi+k-2pi+m+pi;
- the ith point of the polygon  k(
k( m(P)) is 2(2pi+k+m-pi+k)-(2pi+m-pi)=4pi+m+k-2pi+k-2pi+m+pi.
m(P)) is 2(2pi+k+m-pi+k)-(2pi+m-pi)=4pi+m+k-2pi+k-2pi+m+pi.
Thus the arrays  m(
m( k(P)) and
k(P)) and  k(
k( m(P)) are identical.
m(P)) are identical.
It follows from the commutativity of the composition of transformations that the transformations  1,
1,  2, ...,
2, ...,  n-1 can be carried out in any order, the result will always be the same.
n-1 can be carried out in any order, the result will always be the same.
Let H1=(h1,...,hn) and Hn=(g1,...,gn). As every transformation replaces the points by a linear combination, each of the points g1, ..., gn can be expressed as an appropriate linear combination of the points h1, ..., hn. As the sequence of transformations is symmetrical with respect to the cyclic permutation of the indices, the coefficients of the various linear combinations can be obtained from each other by cyclic permutations, that is, there exist such constants a0, a1, ..., an-1 that for all i,
| (4) | gi=a0hi+a1hi+1+...+an-1hi+n-1. |
Now let us prove that a1=a2=...=an-1.
For any integer 0<m<n, let  m denote the permutation (x1,...,xn)
m denote the permutation (x1,...,xn) (xm,x2m,...,xnm). (This is really a permutation if n is a prime.) By substituting the definition, it can be seen that for every integer k and every array P of n numbers,
(xm,x2m,...,xnm). (This is really a permutation if n is a prime.) By substituting the definition, it can be seen that for every integer k and every array P of n numbers,
 k(
k( m(P))=
m(P))= m(
m( km(P)).
km(P)).
By applying this identity (n-1) times, we get
 n-1(
n-1( n-2(...
n-2(... 1(
1( m(H1))...))=
m(H1))...))=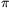 m(
m( (n-1)m(
(n-1)m( (n-2)m(...
(n-2)m(... m(H1)...))).
m(H1)...))).
As n is a prime, each of  1, ...,
1, ...,  n-1 occurs exactly once among the transformations
n-1 occurs exactly once among the transformations  m,
m,  2m, ...,
2m, ...,  (n-1)m. Thus the right-hand side is
(n-1)m. Thus the right-hand side is 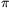 m(Hn)=(gm,g2m,...,gnm).
m(Hn)=(gm,g2m,...,gnm).
Apply the transformations on the left-hand side to the polygon 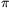 m(H1)=(hm,h2m,...,hnm). It follows from identity (4) that the ith member of the resulting array of n points is
m(H1)=(hm,h2m,...,hnm). It follows from identity (4) that the ith member of the resulting array of n points is
a0him+a1h(i+1)m+...+an-1h(i+n-1)m.
Putting the results together, we have that for all i,
a0him+a1h(i+1)m+...+an-1h(i+n-1)m=
=gim=a0him+a1him+1+...+an-1him+n-1.
The coefficient of h(i+1)m is a1 on the left-hand side, and am on the right-hand side, therefore am=a1. As this is true for all 0<m<n, a1=a2=...=an-1.
The ith edge vector of the polygons H1 and Hn is hi+1-hi, and gi+1-gi=(a0-a1)(hi+1-hi). Thus the two polygons are similar, with a ratio of a0-a1.
Solution 2. This solution uses complex numbers, and the so- called finite Fourier transform . The polygons are considered to be arrays of n complex numbers. In order to make calculations simpler, let us place H1 onto the complex plane so that its centroid should be 0.
If X is an array of n numbers, let Xj denote its jth element. The indices are always meant modulo n, for example, Xn=X0 or X-1=Xn-1.
Arrays of n compex numbers can be added term by term, subtracted, and multiplied by scalars. In addition, define the finite Fourier transform of an array of n numbers as follows. Let 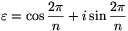 be the first complex nth root of unity. The Fourier transform of the array is the array
be the first complex nth root of unity. The Fourier transform of the array is the array 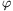 (X), such that for each j,
(X), such that for each j,
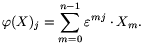
There are several interesting properties and applications of the Fourier transform. See, for example, Algorithms, by P. Gács and L. Lovász. Now we are going to use the following properties:
- For any number c and array X of n numbers, 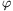 (c.X)=c.
(c.X)=c.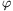 (X).
(X).
- The Fourier transform has an inverse. It is easy to check that,
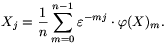
Like in solution 1, let  k be the transformation that reflects every element of an array in its kth successor, that is,
k be the transformation that reflects every element of an array in its kth successor, that is,
 k(X)j=2Xj+k-Xj.
k(X)j=2Xj+k-Xj.
It follows from the definitions of the Fourier transform and  k that for any arrayx of n numbers,
k that for any arrayx of n numbers,
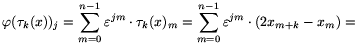
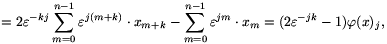
that is,
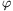 (
( k(x))=(1,2
k(x))=(1,2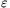 -k-1,2
-k-1,2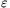 -2k-1,...,2
-2k-1,...,2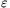 -(n-1)k-1).
-(n-1)k-1).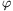 (x).
(x).
Applying this to every 0<k<n, we have
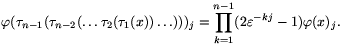
If j=0, then 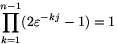 . If 0<j<n, then -- as n is a prime --
. If 0<j<n, then -- as n is a prime -- 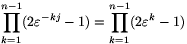 . Let C denote this number.
. Let C denote this number.
Thus we obtain
| (5) | 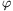 ( ( n-1( n-1( n-2(... n-2(... 2( 2( 1(x))...)))=(1,C,C,...,C). 1(x))...)))=(1,C,C,...,C). (x). (x). |
Consider the arrays  (H1) and
(H1) and  (Hn) of n numbers. Because of the choice of the centroid,
(Hn) of n numbers. Because of the choice of the centroid,  (H1)0=0, and thus (5) can also be written in the following form:
(H1)0=0, and thus (5) can also be written in the following form:
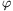 (Hn)=
(Hn)=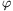 (
( n-1(
n-1( n-2(...
n-2(... 2(
2( 1(H1))...)))=C.
1(H1))...)))=C.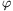 (H1).
(H1).
Hence Hn=C.H1, that is, Hn is obtained from H1 by an enlargement from 0 with a scale factor of C.
Remark. With the polynomial
p(t)=(t-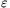 )(t-
)(t-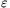 2).(t-
2).(t-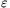 n-1)=xn-1+xn-2+...+x+1,
n-1)=xn-1+xn-2+...+x+1,
we get
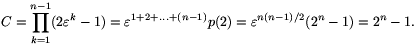
(Using that n is an odd prime, and n(n-1)/2 is divisible by n.)