Exercises and problems in Physics
November 2001
Please read The Conditions of the Problem Solving Competition.
 |
Experimental problem |
M. 228. As is well known, if we stir the tea in a cup the submerged tea leafs gather in the middle in a small heap (against our expectations, because we expect the particles with higher density to drift towards the perimeter of the container). What is the explanation of this phenomenon? Carry out some experiments to prove the explanation. (6 points)
 |
Theoretical problems |
P. 3466. Looking into a convex mirror our nose seems to be disproportionately larger than our ears. Why? (3 points)
P. 3467. Cycling without rest between two towns the journey takes 6 hours. What is the distance between the two towns if our average speed is 16 km/h on level surface, 12 km/h uphill and 24 km/h downhill? (3 points)
P. 3468. In a heat insulated vessel there is tap water of 15 oC. We place in it ice cubes of -15 oC taken out of the deep-freezer. May there be no change of state? When does only a part of the ice melt? In which case does all of the ice melt? In which case does the water freeze? (4 points)
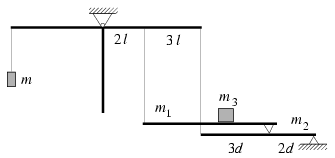
P. 3469. The T shaped rigid body shown in the figure consists of three uniform rods, and can rotate round the horizontal axis t perpendicular to its plane. At the end of the right side rod and at the point dividing it in a 2:3 ratio there are ropes fixed and each of the ropes hold horizontal rods propped up by wedges. The wedge holding the upper rod divides the lower rod in 3:2 ratio. The mass of the upper rod is m1, that of the lower one is m2, and the mass of the body lying on the upper rod is m3. What is the required mass of the body that is to be hung on the end of the left hand side rod so as to keep the balance. The data: m1=2.5 kg, m2=6.0 kg, m3=7.5 kg. (5 points)
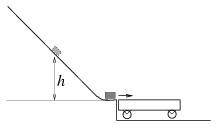
P. 3470. A carriage is joined to the end of a slope as can be seen in the figure. A body released from the slope from height h slides as far as the middle of the carriage. (The friction between the body and the slope and the mass of the wheels of the carriage are negligible.) At what height should the body be released so that it could stop just at the end of the carriage? (4 points)
P. 3471. We make a spiral of 0.6 m radius and 30o slope angle of a thin but sufficiently stiff wire and fix it in a way that its axis is vertical. Then we thread a pierced pearl on the wire and at a given moment we let it slide down. What speed does it gather if the friction coefficient is 0.5? (5 points)
P. 3472. We fix a block to a spring. Hanging the spring at its end the block oscillates with a period of 1 second. Then we put the block on a horizontal table and hurl it towards a wall so that the spring is positioned in between as a bumper. Colliding with the wall the spring contracts then hurls the body back. The block stops exactly when the spring gets its neutral size back. How much time elapsed between the spring touching the wall and the the block stopping? (4 points)
P. 3473. What are the mass percentages in a mixture of hydrogen and helium gases where at isobar dilation 70 % of the absorbed heat from the surrounding environment is converted to internal energy. (4 points)
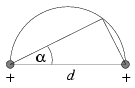
P. 3474. At the endpoints of a line segment
of a length of d there are two identical positive electric
charges. What is the ratio of the electric field strength and the
electric potential in a point characterized by an  angle on the
Thales' circle drawn around the line segment. (4 points)
angle on the
Thales' circle drawn around the line segment. (4 points)
P. 3475. On a bumper at the lower end of a vertically positioned insulator bar shown in the figure there is a pearl of the mass m=10-4 kg and a charge of Q1. Above at a h0=20 cm distance there is another pearl with the same mass m and electric charge Q2 afloat. At a given moment we kick the lower pearl and it starts upwards at a velocity of v0=2 m/s. How close can the lower pearl get to the upper one at most? (The pearls can move along the bar without friction.) (6 points)

P. 3476. In a homogeneous magnetic field there is an electron moving in a circular orbit. Can the magnetic induction vector generated by the moving electron be greater in the middle of the circle than the magnetic induction vector of the homogeneous field? (5 points)
P. 3477. Using thin slats we construct a triangle shaped frame with sides a, b and c. The overall mass of the frame is m. What is the inertial momentum of the frame related to an axis perpendicular to the triangle and crossing the frame in its centre of mass? (5 points)
Send your solutions to the following address:
- KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary
