New exercises and problems in Mathematics
November 2001

Please read The Conditions of the Problem Solving Competition.

New exercises in November 2001

Maximum score for each exercise (sign "C") is 5 points.

C. 645. Two players play the following game. They take turns in taking matches from a heap that initially contains 7 matches. In each step, a player can take one, two or three matches. The game continues until there are no matches left. The winner is the player holding an even number of matches at the end. Which player has a winning strategy, the one who starts or his opponent? How should he play in order to win?

Kvant

C. 646. In the sequence obtained by omitting the squares from the sequence of natural numbers, what is the 2001st term? Which term of the sequence is the number 2001?

Proposed by: P. Nádor, Pécs

C. 647. We have graphed the function f(x)=1/x in the coordinate plane. We want to alter the units on the coordinate axes so that the curve should represent the function g(x)=2/x. How should the new unit be set if it is to be the same on both axes?

C. 648. Evaluate 2^log₆18^.3^log₆3.

C. 649. The area of the base of a truncated pyramid is 8 cm², and the area of the cover is 1 cm². The pyramid is cut with a plane parallel to the base into two parts of equal volumes. Find the area of the intersection.

Proposed by: Á. Besenyei, Tatabánya

New problems in November 2001

The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3492. The numbers 1, 2, ..., n² are written in increasing order into an nxn array:

1	2	...	n
n+1	n+2	...	2n
...	...		...
n²-n+1	n²-n+2	...	n²

A number is selected from each row, such that no two numbers belong to the same column. What are the possible values of the sum of the selected numbers? (3 pont)

IMC 8, Prague, 2001

B. 3493. Two players play the following game. They take turns in taking matches from a heap that initially contains an odd number of matches. In each step, a player can take one, two or three matches. The game continues until there are no matches left. The winner is the player holding an even number of matches at the end. Which player has a winning strategy, the one who starts or his opponent? (5 points)

Kvant

B. 3494. Prove that if the equation ax³+bx²+cx+d=0 has three different positive roots, then bc<3ad. (4 points)

Proposed by: G. Bakonyi, Budapest

B. 3495. The sides of rectangle ABCD are AB=3, BC=2. P is the point on side AB for which the line PD touches the circle of diameter BC. Denote the point of tangency by E. The line passing through E and the centre of the circle intersects the side AB at Q. Find the area of the triangle PQE. (3 points)

Proposed by: L. Gerőcs, Budapest

B. 3496. P is a point in the interior of the square ABCD, such that AP:BP:CP=1:2:3. Find the measure of the angle APB. (4 points)

B. 3497. For the real number x, {x}+{x^-1}=1. Calculate {x²⁰⁰¹}+{x^-2001}. (4 points)

Proposed by: Á. Besenyei, Tatabánya

B. 3498. In triangle ABC, there is a right angle at vertex C. The bisectors of the acute angles intersect the opposite sides at the points M and N respectively. Let P be the intersection of segment MN and the altitude drawn from C. Prove that the length of CP is equal to the radius of the inscribed circle. (4 points)

Proposed by: I. Merényi, Budapest

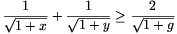B. 3499. The geometric mean of the positive numbers x and y is g. Prove that if g $ge$ 3, then ${1\over\sqrt{1+x}}+{1\over\sqrt{1+y}}\geq{2\over\sqrt{1+g}}$ , and if g $le$ 2, then $\displaystyle {1\over\sqrt{1+x}}+{1\over\sqrt{1+y}}\leq{2\over\sqrt{1+g}}$. (5 points)

B. 3500. A line of one hundred boys and another line of one hundred girls are standing facing one another. Every boy chooses a girl (it is allowed for more than one boy to choose the same girl) and walks up to her along the shortest path. In doing so, their paths do not cross. Then the boys go back to their places, and now the girls do the same, making sure that their paths do not cross as they are walking up to the chosen boy. Prove that there is a girl and a boy who chose each other. (4 points)

B. 3501. Given the points A(1, 1, 1) and P(1, 1, 0) in the coordinate space, rotate the point P about the ray OA in the positive direction through an angle of 60^o. Find the coordinates of the rotated point. (4 points)

New advanced problems in November 2001

Maximum score for each advanced problem (sign "A") is 5 points.

A. 275. The numbers 1², 2², 3², ..., (n²)² are written in increasing order into an nxn array:

1²	2²	...	n²
(n+1)²	(n+2)²	...	(2n)²
...	...		...
(n²-n+1)²	(n²-n+2)²	...	(n²)²

A number is selected from each row, such that no two numbers belong to the same column. What are the possible values of the sum of the selected numbers?

From the idea of T. Terpai

A. 276. The product of the positive numbers x₁, ..., x_n is 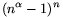$(n^\alpha-1)^n$ , where $alpha$ $ge$ 1 is a real number. Prove that

$\displaystyle \sum_{i=1}^n{1\over(x_i+1)^{1/\alpha}}\ge1.$

A. 277. Let H₁ be an n-sided polygon. Construct the sequence H₁, H₂, ..., H_n of polygons as follows. Having constructed the polygon H_k, H_k+1 is obtained by reflecting each vertex of H_k through its k-th neighbour in the counterclockwise direction. Prove that if n is a prime, then the polygons H₁ and H_n are similar.

Send your solutions to the following address:

or by e-mail to:

solutions@komal.elte.hu

Already signed up?
New to KöMaL?