New exercises and problems in Mathematics
December 2001

Please read The Conditions of the Problem Solving Competition.

New exercises in December 2001

Maximum score for each exercise (sign "C") is 5 points.

C. 650. In a picture gallery, the price of the picture frames is proportional to the price of the paintings in them. In order to reduce the differences between the prices of the pictures, the manager interchanges the frames of two pairs of pictures. In one case, one picture, that was originally five times as expensive as the other one, is now only three times as expensive. How does the ratio of the prices of the "Winter Landscape" and the "Naughty Boy" change if the "Winter Landscape" originally cost nine times as much as the "Naughty Boy"?

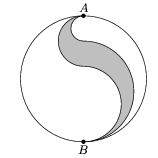
C. 651. The shaded figure in the diagram is bounded by semicircles. The diameter AB has a segment of length 1/5 units within the shaded figure. Find the perimeter and area of the shaded figure.

C. 652. Let s be a positive integer of an odd number of digits. Let f denote the number that consists of the digits of f, but in opposite order. Prove that s+f is divisible by 11 if and only if s is also divisible.

C. 653. For how many different values of the parameter p do the following simultaneous equations have exactly one solution? x²-y²=0, xy+px-py=p²

C. 654. f_a, f_b and f_c denote the lengths of the interior angle bisectors in a triangle of sides a, b, c, and area T . Prove that 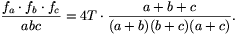${{f_a\cdot f_b\cdot f_c}\over abc}=4T\cdot{{a+b+c}\over{(a+b)(b+c)(a+c)}}.$

Proposed by:: G. Kovács, Budapest

New problems in December 2001

The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3502. The semicircle of diameter AB intersects the altitude drawn from vertex C of triangle ABC at point C₁, and the semicircle of diameter BC intersects the altitude from A at point A₁. Prove that BC₁=BA₁. (3 points)

B. 3503. Given are the segments a,b,c,d and f. Assuming that there exists a quadrilateral whose sides are a,b,c,d and the length of the segment connecting the midpoints of two opposite sides is f construct the quadrilateral. (4 points)

B. 3504. If S(n) denotes the sum of the digits of the number n in decimal notation, and U_k=11...1 is the number that consists of k ones, find the values of k for which S(U_k²)=(S(U_k)²). (4 points)

B. 3505. A regular octagon is subdivided into parallelograms. Prove that there is a rectangle among the parallelograms. (5 points)

B. 3506. f is a polynomial for which f(x²+1)-f(x²-1)=4x²+6. Find the polynomial f(x²+1)-f(x²). (4 points)

B. 3507. Let f(x) be a polynomial of integer coefficients, p and q coprime numbers such that q$\displaystyle ne$0. Prove that if p/q is a root of the polynomial, then f(k) id divisible by p-kq for every integer k. Is the converse of the statement also true? (4 points)

B. 3508. The triangles ABC and A₁B₁C₁ are symmetric about a line. Draw a parallel through A₁ to BC, through B₁ to AC, and finally, through C₁ to AB. Prove that the three lines all pass through a common point. (4 points)

B. 3509. Prove that, if 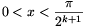$0<x<{{\pi}\over{2^{k+1}}}$ , then 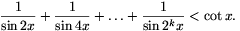${1\over{\sin2x}}+{1\over{\sin4x}}+\dots+{1\over{\sin2^kx}}<\cot x.$ (3 points)

Proposed by:: J. Balogh, Kaposvár

B. 3510. Consider the planes through the vertices of tetrahedron ABCD that are parallel to the opposite faces. The four planes enclose another tetrahedron. Prove that A, B, C and D are the centroids of the faces of the new tetrahedron. (3 points)

B. 3511. For the non-negative numbers a, b, c and d, a$\displaystyle le$1, a+b $le$ 5, a+b+c$\displaystyle le$14, a+b+c+d $le$ 30. Prove that $\displaystyle \sqrt a+\sqrt b+\sqrt c+\sqrt d\leq10$. (5 points)

New advanced problems in December 2001

Maximum score for each advanced problem (sign "A") is 5 points.

A. 278. P is a point on the extension of the diagonal AC of rectangle ABCD beyond C, such that BPD$\displaystyle angle$=CBP$\displaystyle angle$. Find the ratio PB:PC.

A. 279. Are there such rational functions f and g that (f(x))³+(g(x))³=x?

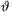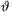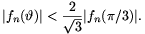
A. 280. For each positive integer n, let f_n($\displaystyle vartheta$)=sin$\displaystyle vartheta$^.sin(2 $vartheta$ )^.sin(4$\displaystyle vartheta$)^....^.sin(2ⁿ $vartheta$ ). For all real $\displaystyle vartheta$ and all n, prove that $|f_n(\vartheta)|<{2\over\sqrt3}|f_n(\pi/3)|.$

IMC 8, Prague, 2001

Send your solutions to the following address:

or by e-mail to:

solutions@komal.elte.hu

Already signed up?
New to KöMaL?