New exercises and problems in Mathematics
February 2002

Please read The Conditions of the Problem Solving Competition.

New exercises in February 2002

Maximum score for each exercise (sign "C") is 5 points.

C. 660. In how many different ways is it possible to select two fields of a 8x8 chessboard, such that the midpoint of the segment joining the centres of the two fields should also be the centre of a field?

C. 661. On what condition will the product of a number ending in 9 and a number ending in 7 end in 63?

C. 662. The volume of a brick is 8 cm³. If each edge is increased by 1 centimetre, the volume of the new brick will be 27 cm³. What will be the volume if each edge is now increased again by 1 centimetre?

C. 663. A sheet of paper in the shape of an acute triangle has the vertex with the largest angle torn off. On the remaining piece of paper, construct the radius of the circumscribed circle of the triangle.

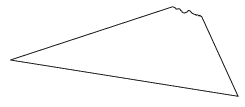
Suggested by S. Róka, Nyíregyháza

C. 664. Determine the distance between the tangents drawn to the parabolas y=x²+1 and x=y²+1 parallel to the line y=x.

Correction.

Exercise C. 658. in the previous issue contains an error. The correct problem is:

C. 658. Solve the simultaneous equations

$\displaystyle {1\over x}+{1\over y}={1\over z}$

$\displaystyle {1\over x+15}+{1\over y-6}={1\over z}$

$\displaystyle {1\over x+24}+{1\over y-15}={1\over z}.$

The new deadline for this problem is 15 March 2002.

New problems in February 2002

The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3522. Solve the following equation on the set of integers: 2x⁴+x²y²+5y²=y⁴+10x². (3 points)

B. 3523. Given a semicircle, consider the triangles in which the diameter of the semicircle is contained in one side, and the other two sides are tangent to the semicircle. Which of these triangles has minimum area? (4 points)

B. 3524. The sum of the real numbers x and y is 1. Find the maximum value of xy⁴+x⁴y. (3 points)

B. 3525. Prove that there are infinitely many composite numbers in the sequence 1,31,331,3331,... . (4 points)

B. 3526. F is the midpoint of side BC of a rectangle ABCD, and H divides side CD in the ratio 1:2, CH being the shorter part. How large may the angle HAF be? (4 points)

B. 3527. Given a trapezium in which the other two sides are not parallel, construct, using a straight edge only, a line whose segment between the non-parallel sides is divided into three equal parts by the diagonals of the trapezium. (5 points)

B. 3528. Let $\displaystyle alpha$ and $\displaystyle beta$ be acute angles such that sin²$\displaystyle alpha$+sin²$\displaystyle beta$<1. Prove that sin² $alpha$ +sin²$\displaystyle beta$<sin²( $alpha$ + $beta$ ). (4 points)

B. 3529. The sum of the first few terms in a geometric progression is 11, the sum of their squares is 341, and the sum of their cubes is 3641. Find the terms of the sequence. (5 points)

(Suggested by Á. Besenyei, Budapest)

B. 3530. Evaluate 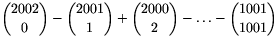${2002\choose0}-{2001\choose1}+{2000\choose2}-\dots-{1001\choose1001}$ . (5 points)

B. 3531. The inscribed circle of a triangle ABC is centred at O, and touches the sides at A₁, B₁, C₁ (in customary notation). The lines A₁O, B₁O, C₁O intersect the segments B₁C₁, C₁A₁, A₁B₁ at the points A₂, B₂, C₂, respectively. Prove that the lines AA₂, BB₂ és CC₂ are concurrent. (5 points)

(Suggested by Á. Besenyei, Budapest)

New advanced problems in February 2002

Maximum score for each advanced problem (sign "A") is 5 points.

A. 284. Let f be a function defined on the subsets of a finite set S. Prove that if f(S\A)=f(A) and max(f(A),f(B))$\displaystyle ge$f(A$\displaystyle cup$B) for all subsets A, B of S, then f assumes at most |S| distinct values.

(Miklós Schweitzer Memorial Competition, 2001)

A. 285. Prove that if a²+ac-c²=b²+bd-d², for the integers a>b>c>d>0, then ab+cd is a composite number.

A. 286. Find all continuous functions 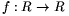$f:R\to R$ such that

$\displaystyle f\left({x+y\over1+xy}\right)={f(x)f(y)\over|1+xy|},$

where 1+xy$\displaystyle ne$0. (based on the idea of Z. Győrfi and G. Ligeti)

Send your solutions to the following address:

or by e-mail to:

solutions@komal.elte.hu

Already signed up?
New to KöMaL?

New exercises and problems in MathematicsFebruary 2002