Solutions for advanced problems "A" in March, 2002

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

A. 287. Someone has drawn an ellipse on a sheet of paper, and he has also marked the endpoints of its axes. The major axis is twice as long as the minor axis. Find a construction method for dividing any given acute angle into three equal parts, using a pair of compasses, a straight edge, and the given ellipse only.

Solution. Let 3$\displaystyle alpha$ be the angle to be trisected, and let the equation of the ellipse in rectangular coordinates be x²+4y²=1.

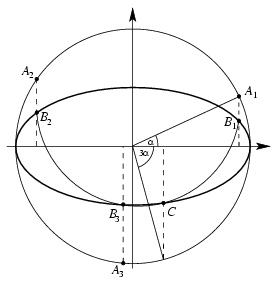
Let A_i=(cos($\displaystyle alpha$+(i-1)^.120^o);sin($\displaystyle alpha$+(i-1)^.120^o)) and $\displaystyle B_i=(\cos(\alpha+(i-1)\cdot120^\circ);{1\over2}\sin(\alpha+(i-1)\cdot120^\circ))$ (i=1,2,3). The points A_i are on the unit circle, and the points B_i are on the ellipse. The task is to construct these points.

Consider the circle passing through the points B_i. The circle also intersects the ellipse at a fourth point C. With a little calculation, it can be checked that the centre of the circle is $\displaystyle K=\left({3\over16}\cos3\alpha;{3\over8}\sin3\alpha\right)$ and that $\displaystyle C=(\cos3\alpha;{1\over2}\sin3\alpha)$. For a given 3$\displaystyle alpha$, the circle can be constructed, and it intersects the ellipse at the points B_i.

A. 288. Let p be an n degree polynomial, where n$\displaystyle ge$1. Prove that there exist at least n+1 complex numbers yielding 0 or 1 as the value of f. (IMC 7, London, 2000)

Solution. Let z₁, ..., z_k be the complex numbers where the value of p is 0 or 1. Let $\displaystyle mu$_j denote the multiplicity of the root z_j of the polynomial p(z) or p(z)-1. Then the number z_j is a root of p' with a multiplicity of ($\displaystyle mu$_j-1). If multiplicity counts, The polynomials p(z) and p(z)-1 together have 2n roots among the numbers z₁,...,z_k, and the polynomial p' has at most n-1, thus

$\displaystyle mu$₁+...+$\displaystyle mu$_k=2n,   ($\displaystyle mu$₁-1)+...+($\displaystyle mu$_k-1)$\displaystyle le$n-1.

By subtraction, we get k$\displaystyle ge$n+1.

A. 289. Prove that if the function f is defined on the set of positive real numbers, its values are real, and f satisfies the equation

$\displaystyle f\left({x+y\over2}\right)+f\left({2xy\over x+y}\right)=f(x)+f(y)$

for all positive x,y, then

$\displaystyle 2f\big(\sqrt{xy}\big)=f(x)+f(y)$

for every positive number pair x, y. (Miklós Schweitzer Memorial Competition, 2001)

Solution. Let a,b,c,d be positive real numbers. By applying the functional equation several times, we have

f(a)+f(b)+f(c)+f(d)=

$\displaystyle =f\left({a+b\over2}\right)+f\left({2ab\over a+b}\right)+f\left({c+d\over2}\right)+f\left({2cd\over c+d}\right)=$

$\displaystyle =f\left({{a+b\over2}+{c+d\over2}\over2}\right)+f\left({2{a+b\over2}\cdot{c+d\over2}\over{a+b\over2}+{c+d\over2}}\right)+$

$\displaystyle \qquad+f\left({{2ab\over a+b}+{2cd\over c+d}\over2}\right)+f\left({2{2ab\over a+b}\cdot{2cd\over c+d}\over{2ab\over a+b}+{2cd\over c+d}}\right)=$

$\displaystyle f\left({a+b+c+d\over4}\right)+f\left({(a+b)(c+d)\over a+b+c+d}\right)+$

$\displaystyle \qquad+f\left({abc+abd+acd+bcd\over(a+b)(c+d)}\right)+f\left({4abcd\over abc+abd+acd+bcd}\right).$

By repeating the above procedure with b and c interchanged, we get

$\displaystyle \qquad=f\left({(a+c)(b+d)\over a+b+c+d}\right)+f\left({abc+abd+acd+bcd\over(a+c)(b+d)}\right).$

Let a=c, b=a²/d and $\displaystyle t={a\over b}+{b\over a}$. It is easy to check that

$\displaystyle {(a+b)(c+d)\over a+b+c+d}={abc+abd+acd+bcd\over(a+b)(c+d)}=a,$

$\displaystyle {(a+c)(b+d)\over a+b+c+d}=a\cdot{2t\over2+t},$

and finally

$\displaystyle {abc+abd+acd+bcd\over(a+c)(b+d)}=a\cdot{2+t\over2t}.$

Substitution of the results into (1) gives

t can be any number not smaller than 2, and $\displaystyle {2t\over2+t}$ can be any number not smaller than 1. Thus for every number pair x$\displaystyle ge$y there exist the numbers a and t, such that $\displaystyle a\cdot{2t\over2+t}=x$, $\displaystyle a\cdot{2+t\over2t}=y$ and $\displaystyle \sqrt{xy}=a$.