Exercises and problems in Physics
March 2002

Please read The Conditions of the Problem Solving Competition.

Correction

Problem P. 3486. in December, 2001 contained a mistake. Now the problem is issued again. You can send your solution for the corrected problem together with the problems in March. (Your score will be counted in December.)

P. 3486. The binding energy of the ¹⁴N nucleus is 16.76 pJ and the ¹⁴C nucleus is 16.86 pJ. Which nucleus is the decay product of the other, and why? (5 points)

Experimental problem

M. 232. Hang a homogeneous metal bar symmetrically using two strong threads as seen in the figure. How does the period of this somewhat distorted system depend on distances l and b. (6 points)

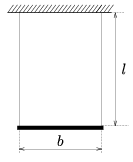
Theoretical problems

P. 3509. Is it possible that a freely falling body covers twice the distance in the last second of the fall than in the previous second? (3 points)

P. 3510. A 150 kg piston closes 32 g of oxygen gas of a temperature of 0 ^oC in a vertical cylinder of base area of 4 dm². The air pressure outside is 1.01^.10⁵ Pa. The axis of the cylinder is vertical, and the piston can move in it without friction. At what height is the piston in rest? How much heat is to be transferred to the gas to raise the piston 20 cm? (4 points)

P. 3511. There is a line pendulum of length l hanging from a nail sticking out of a vertical wall. Release the pendulum from the horizontal position. When its angular separation from the horizontal is $\displaystyle alpha$ the line hits another nail and from here the small body at the end of the line moves along an arc around this second nail. How far can the second nail be from the first one if the body goes all along this new circular path? (4 points)

P. 3512. One side of a building is exposed to heavy sunshine. What is the direction of the draft inside the building if we open one window on both the sunlit and the shady side? (3 points)

P. 3513. Estimate the resistance caused by rain under no wind conditions for a running car. Suppose, that in half an hour there has been 10 mm of precipitation, the diameter of a rain drop is 2 mm, the frontal area of the car is 1.5 m², and its velocity is 90 km/h. What is the ratio of the rain and air densities? (5 points)

P. 3514. Examine the motion of a solid cylinder of mass m=4 kg moving down a long $\displaystyle alpha$=30^o angle slope having two different surfaces. The initial velocity of the cylinder is zero. The first section of the slope is very smooth, the friction coefficient is $\displaystyle mu$₁=0 here, while on the second section it is $\displaystyle mu$₂=tan $alpha$ . The cylinder arrives on this second section after it has descended h=1.8 m in the vertical direction.

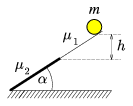
a) How long after starting will the cylinder roll cleanly?

b) How much mechanical energy is lost during the motion of the cylinder? (5 points)

P. 3515. In a parallel-plate capacitor the area of each plate are 1500 cm², and the distance of the plates is 20 mm. After switching on a 250 V power supply we push a 5 mm thick metal plate and a 5 mm thick glass plate ( $varepsilon$ _rel=5) between the plates. How much work is done while pushing in the plates? (5 points)

P. 3516. One half of the square cross-section ring seen in the figure is made of aluminium and the other of copper. The inner radius of the ring is 8 cm and the outer is 10 cm. It is in a homogeneous magnetic field perpendicular to its plane, where the magnetic induction is 0.1 T. How much electric charge accumulates at the joints if the magnetic induction is linearly decreased to zero within 2 seconds? (6 points)

P. 3517. The decay half-time of a radioactive source is T, and initially it resides in r₀ distance of our radiation counter. Then it starts moving towards us in a way that the count number does not change on the counter. Give the distance of the source and the counter as a function of time. What was the initial velocity of the radioactive source (The absorption in the air is neglected here.)? (5 points)

P. 3518. In the 19th century people thought that the Sun is a burning block of coal, which loses its energy through radiation. On the Earth the intensity of the radiation of the Sun is 1400 W/m². Let us suppose that the intensity will not change in the future. The mass of the Sun is 2^.10³⁰ kg, its distance from the Earth is 1.5^.10¹¹ m and the caloric value of coal is 30 MJ/kg. How long would the Sun shine, if it really were a burning coal block? (The result of this calculation surprised the scientists at that time as well.) (4 points)

P. 3519. In the assembly seen in the figure, the piston of the lower cylinder is initially at a height of 10 cm. Under the cylinder there is 20 ^oC nitrogen and above it there is mercury which fills in the rubber hose and has its free surface in the upper vessel 2 meters above the piston. The base area of the cylinder is 100 cm², the piston is weightless and the nitrogen can expand to a 30 cm height. The air pressure outside is 10⁵ Pa. While heating the nitrogen the piston rises and we make the upper vessel sink continuously so that while the piston rises 1 mm, the upper level of the mercury drops 9 mm. Continue this while the nitrogen absorbs heat. How much is the absorbed heat? How much is the top temperature of the nitrogen? (6 points)

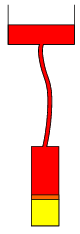
Send your solutions to the following address:

or by e-mail to:

solutions@komal.elte.hu

Already signed up?
New to KöMaL?