New exercises and problems in Mathematics
April 2002

Please read The Conditions of the Problem Solving Competition.

New exercises in April 2002

Maximum score for each exercise (sign "C") is 5 points.

C. 670. We have arranged the first nine positive integers in a 3x3 table, using each of them only once. Suppose that the seven three-digit numbers represented by the rows left to right, by the columns top to bottom, and by the diagonal from the upper left corner are all divisible by 11. What may be the value of the three-digit number represented by the diagonal starting at the upper right corner? (Suggested by S. Kiss, Nyíregyháza)

C. 671. We have placed two jam jars into a cooking pot of diameter 36 cm. The radii of the jars are 6 cm and 12 cm. What is the maximum possible radius of a third jam jar to be placed next to them in the pot?

C. 672. The lengths of the edges from vertex A of a cuboid are 1, 2, and 3 units. Consider the triangle formed by the other endpoints of these edges. Determine the distance of point A from the plane of the triangle.

C. 673. A number is selected out of 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 at random, and then a number is selected again. (It is allowed to select the same number twice.) Which is greater, the probability that the sum of the two numbers is divisible by 3, or the probability that their difference is divisible by 3?

C. 674. Solve the following equation:

\(\displaystyle {x\over20}=\left({5\over2}\right)^{\log_x50}.\)

New problems in April 2002

The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3542. Prove that if a number of the form 111...1 is divisible by 7 then it is also divisible by 37. (3 points)

B. 3543. There is a square hole in a square sheet of paper. Each side of the hole is extended in the counterclockwise direction. Suppose that the rays obtained in this way cut the sheet into four quadrangles, as shown in the figure. Prove that it is possible to assemble the four pieces in a different way to form a square with a square hole in it.

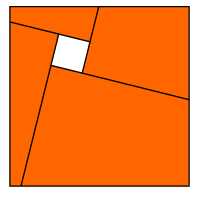
(4 points)

(Based on the idea of P. Gál)

B. 3544. Prove that every triangle has an escribed circle whose radius is at least three times the radius of the incircle. (3 points)

B. 3545. Prove that

\(\displaystyle {n^2-n\over2}\leq\big\{\sqrt1\big\}+\big\{\sqrt2\big\}+\ldots+\big\{\sqrt{n^2}\big\}\leq{n^2-1\over2},\)

where {x} denotes the fractional part of x (i.e. the difference of x and the greatest integer not greater than x). (4 points)

B. 3546. A plane intersects a cube in a hexagon ABCDEF. Given that the diagonals AD, BE, CF of the hexagon are concurrent, prove that the plane passes through the centre of the cube. (5 points)

B. 3547. Prove that if

\(\displaystyle f(x+1)+f(x-1)=\sqrt2f(x)\)

is true for every real x then the function f is periodic. (4 points)

B. 3548. Each term of an infinite arithmetic sequence of different positive integers is divided by its greatest prime factor. Is it possible to obtain a bounded sequence in this way? (4 points)

B. 3549. Prove that for every real number x,

cos cos x\(\displaystyle ge\)|sin x|.

(4 points) (Suggested by: L. Szobonya, Budapest)

B. 3550. The altitudes from the vertices A and B of triangle ABC intersect each other at M, and they intersect the opposite sides at A₁ and B₁, respectively. The line A₁B₁ intersects the side AB at D. Prove that the line DM is perpendicular to the median from vertex C. (5 points)

B. 3551. Let a, b, c, d be positive integers, such that

a²+b²+ab=c²+d²+cd.

Prove that a+b+c+d is a composite number. (5 points)

New advanced problems in April 2002

Maximum score for each advanced problem (sign "A") is 5 points.

A. 290. Given a finite number of square sheets of paper with a total area of 4 units, prove that it is possible to cover a unit square with them. (Allan Wilson, England)

A. 291. Solve the equation

\(\displaystyle x=\sqrt{2+\sqrt{2-\sqrt{2+x}}}.\)

A. 292. In a metropolis, there are n underground lines (n>4). At most three lines meet at any station, and for any two lines there is a third line such that one can make a transfer to it from each of the two lines. Prove that there are at least \(\displaystyle {5\over6}(n-5)\) underground stations.

Send your solutions to the following address:

or by e-mail to:

solutions@komal.elte.hu

Already signed up?
New to KöMaL?