New exercises and problems in Mathematics
May 2002

Please read The Conditions of the Problem Solving Competition.

New exercises in May 2002

Maximum score for each exercise (sign "C") is 5 points.

C. 675. Is there a square number in which the last two digits are both odd?

C. 676. The length of side AB of the rectangle ABEF is 1 unit, and the length of side BE is 3 units. The points C and D divide side BE into three equal parts. Show that BAC $\angle$ +BAD$\displaystyle \angle$+BAE $\angle$ =180^o.

C. 677. Find the integers a and b, given that a⁴+(a+b)⁴+b⁴ is a square number.

C .678. In a triangle ABC, AC=1, ABC$\displaystyle \angle$=30^o, BAC $\angle$ =60^o, and D denotes the foot of the altitude from vertex C. Find the distance between the centres of the inscribed circles of the triangles ACD and BCD.

C. 679. Given three spheres that pairwise touch each other and also touch the plane S, determine the radius of the sphere that has its centre on the plane S, and that touches all the three spheres.

New problems in May 2002

The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3552. Each member of the sequence a₁, a₂, ..., a_2n+1 is either 2, 5 or 9. No two consecutive members are equal, and a₁=a_2n+1. Prove that a₁a₂-a₂a₃+a₃a₄-a₄a₅+...-a_2na_2n+1=0. (3 points)

B. 3553. In a triangle ABC, the altitude from vertex A, the angle bisector from vertex B, and the median from vertex C intersect the opposite sides at the points A₁, B₁, C₁, respectively. Prove that if the triangle A₁B₁C₁ is equilateral, then the triangle ABC is also equilateral. (4 points)

B. 3554. The diagonals of parallelogram ABCD intersect at point M. The circle passing through the points A, M, B touches the line BC. Prove that the circle through the points B, M, C touches the line CD. (3 points)

B. 3555. A company consists of 2n+1 people. For every group of n members, there exists a member of the company who does not belong to the group, but who knows every member of the group. Acquaintances are considered to be mutual. Prove that there is a member of the company who knows everybody. (5 points)

B. 3556. Given two sides and the bisector of the exterior angle at their common vertex, construct the triangle. (4 points)

B. 3557. Is it possible for a perfect cube to start with 2002 ones in decimal notation? (4 points)

B. 3558. Is there a non-constant polynomial of integer coefficients, such that its value is a power of 2 at every positive integer? (4 points)

(Inspired by a problem of the National Competition, 2002)

B. 3559. e₁, e₂, ..., e_n are lines in the plane. Through an arbitrary point P₁ of line e₁, drop a perpendicular to the line e₂, and denote the foot of the perpendicular by P₂. Let P₃ be the foot of the perpendicular from P₂ onto e₃, and so on. Finally, let P_n+1 denote the foot of the perpendicular from P_n onto e₁. Prove that there exists a point P₁ on the line e₁, such that the point P_n+1 obtained in this way should coincide with P₁. (4 points)

B. 3560. Prove that no matter how we leave 89 numbers out of the first 2002 positive integers, the set of the remaining numbers will contain 20 elements, such that their sum is also among the remaining numbers. (5 points)

B. 3561. A convex polyhedron has exactly three edges meeting at each vertex. Given that all but one of the faces of the polyhedron are known to have circumscribed circles, prove that all the faces have circumscribed circles. (5 points)

New advanced problems in May 2002

Maximum score for each advanced problem (sign "A") is 5 points.

A. 293. Prove that for every integer m$\displaystyle \ge$2 there exists a pair of positive integers a and b, such that in base-m notation, a and b together contain exactly the same number of each digit as the number a^.b. (L. Szobonya, Budapest)

A. 294. Define the sequence a₁,a₂,... with the following recursion:

$\displaystyle a_1=1, \quad a_{n+1}={a_1a_n+a_2a_{n-1}+\dots+a_na_1\over n+1}.$

Prove that the sequence 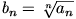$b_n=\root{n}\of{a_n}$ is convergent.

A. 295. Positive numbers x₁,x₂...,x_n satisfy

$\displaystyle {1\over1+x_1}+{1\over1+x_2}+\dots+{1\over1+x_n}=1.$

Prove that

$\displaystyle \sqrt{x_1}+\sqrt{x_2}+\dots+\sqrt{x_n}\ge(n-1) \left({1\over\sqrt{x_1}}+{1\over\sqrt{x_2}}+\dots+ {1\over\sqrt{x_n}}\right).$

(Vojtech Jarník Mathematical Competition, Ostrava, 2002)

Send your solutions to the following address:

or by e-mail to:

solutions@komal.elte.hu

Already signed up?
New to KöMaL?