 |
Solutions for advanced problems "A" in November, 2002 |
In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.
A. 302. Given the unit square ABCD and the point P on the plane, prove that
\(\displaystyle 3AP+5CP+\sqrt5(BP+DP)\ge6\sqrt2.\)
Solution 1 Let \(\displaystyle f(P)=3AP+5CP+\sqrt5(BP+DP)\) for any point P of the plane . Since each term is a convex (below) function of P, the function f is also convex. Thus, if a point is found where the function is differentiable and the gradient is the zero vector, the function has an absolute minimum there.
The gradient of the function is
\(\displaystyle \mathop{\rm grad}f=3{\overrightarrow{AP}\over|AP|}+ 5{\overrightarrow{CP}\over|CP|}+ \sqrt5\left({\overrightarrow{BP}\over|BP|}+ {\overrightarrow{DP}\over|DP|}\right).\)
Since the positions of the points B and D symmetrical, we should look for the minimum point on the diagonal AC.
By a little calculation, we can show that the minimum occurs at the point lying closer to C and dividing the diagonal AC in a 3:1 ratio. At that point, therefore, the gradient is 0, and it is easily obtained that the value of the function is \(\displaystyle 6\sqrt2\). This is the smallest value of the function.
Solution 2 (This is the origin of the problem). Let A=(0,0), B=(1,0), C=(1,1) and D=(0,1). Let E=(1,5/6), F=(0,1/2), Q=(3/4,3/4), U=(-3/10,2/5) and V=(3/2,1). It is easy to check that the points U,F,Q,E,V all lie on a line in this order. The points A,Q,D,U lie on a circle, and so do the points B,V,C,Q.
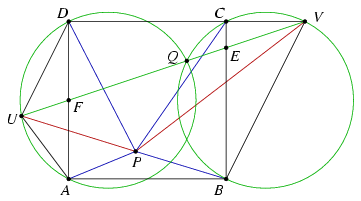
A Ptolemy's theorem states that AU.DP+DU.AP\(\displaystyle \ge\)AD.UP=UP, and equality occurs if and only if the points A,P,D,U in this order are concyclic. Similarly, BV.CP+CV.BP\(\displaystyle \ge\)BC.VP=VP; and equality occurs if and only if B,V,C,P are concyclic. Finally, UP+VP\(\displaystyle \ge\)UV from the triangle inequality.
The lengths of the line segments in the above inequalities are \(\displaystyle AU=CV={1\over2}\), \(\displaystyle DU={3\sqrt5\over10}\), \(\displaystyle BV={\sqrt5\over2}\) and \(\displaystyle UV={3\sqrt{10}\over5}\). Thus
\(\displaystyle {1\over2}\cdot DP+{3\sqrt5\over10}\cdot AP+ {\sqrt5\over2}\cdot CP+{1\over2}\cdot BP\ge UP+VP\ge{3\sqrt{10}\over5}.\)
Multiplication by \(\displaystyle 2\sqrt5\) yields the statement of the problem.
If P=Q, equality holds.
A. 303. x, y are non-negative numbers, and x3+y4\(\displaystyle \le\)x2+y3. Prove that x3+y3\(\displaystyle \le\)2.
Solution.
2-x3-y3=3(x2+y3-x3-y4)+(x-1)2(2x+1)+(y-1)2(3y2+2y+1)\(\displaystyle \ge\)0.
A. 304. Find all functions R+\(\displaystyle \mapsto\)R+, such that
f(x+y)+f(x).f(y)=f(xy)+f(x)+f(y)?
Solution. Substitute x=y=2: f(4)+f(2)2=f(4)+2f(2). Hence f(2)=0.
Substitute x=y=1: f(2)+f2(1)=3f(1), that is f2(1)-3f(1)+2=0. This is a quadratic equation in f(1) that has two roots 1 and 2.
Case 1: f(1)=1. We shall prove that in this case the function f is additive as well as multiplicative, that is, f(u+v)=f(u)+f(v) and f(uv)=f(u)f(v) for all u,v. It follows from the equation (1) that it is enough to prove one of the two properties. Let us prove the additive property.
Substitute y=1 in the equation: f(x+1)+f(x).f(1)=2f(x)+f(1), that is, f(x+1)=f(x)+1 for all positive x.
Now let u and v be two arbitrary positive numbers. Apply the equation (1) to the number pairs x=u, y=v/u and x=u, y=v/u+1, too:
f(u+v/u)+f(u).f(v/u)=f(v)+f(u)+f(v/u),
and
f(u+v/u+1)+f(u).f(v/u+1)=f(u.(v/u+1))+f(u)+f(v/u+1),
f(u+v/u)+1+f(u)(f(v/u)+1)=f(u+v)+f(u)+f(v/u)+1.
f(u+v)=f(u)+f(v) is obtained by subtracting the two equations.
It follows from the additive property that f(n)=n for all positive integers n, and it follows from the multiplicative property that f(k/n)=f(k)/f(n)=k/n for all integers k,n. Thus f(q)=q for all positive rational numbers q. Additivity also implies that the function is monotonic: f(x)<f(x)+f(y-x)=f(y) for x<y.
The only such function is the identity: f(x)=x.
Case 2: f(1)=2. We shall show that the function is constant: f(u)=2 for all positive u.
Substitute y=1 into the equation again: f(x+1)+2f(x)=2f(x)+2, thus f(x+1)=2. That proves the statement for u>1.
Now let u be an arbitrary real number. If v is a number such that v, uv and u+v are all greater than 1. The equation states that f(u+v)+f(u).f(v)=f(uv)+f(u)+f(v), that is, 2+f(u).2=2+f(u)+2. Hence f(u)=2.
Thus the equation is satisfied by two functions: f(x)=x and f(x)=2.
