New exercises and problems in Mathematics
November 2002

Please read The Conditions of the Problem Solving Competition.

New exercises

Maximum score for each exercise (sign "C") is 5 points.

C. 690. Is it possible for the sum of the volumes of three cubes of integer edges to be 2002 units?

C. 691. Express in mm² the area of Hungary on a globe of radius 25 cm.

C. 692. For the real numbers x, y, z, (1) x+2y+4z $\ge$ 3 and (2) y-3x+2z$\displaystyle \ge$5. Prove that y-x+2z$\displaystyle \ge$3.

C. 693. In what interval may the apex angle of an isosceles triangle vary if a triangle can be constructed out of its altitudes?

C. 694. Evaluate the sum [log₂1]+[log₂2]+[log₂3]+...+[log₂2002].

Suggested by Á. Besenyei, Budapest

New problems

The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3582. Solve the equation 3xyz-5yz+3x+3z=5 on the set of natural numbers. (3 points)

B. 3583. The incentre of a triangle ABC is connected to the vertices. One of the resulting three triangles is similar to the original triangle ABC. Find the angles of the triangle ABC. (3 points)

B. 3584. Write down all the integers from 1 to 10^n-1, and let A denote the number of digits hence written down. Now write down all the integers from 1 to 10ⁿ, and let B denote the number of zeros written down this time. Prove that A=B. (4 points)

B. 3585. Find the possible values of the parameter a, such that the inequality 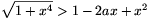$\sqrt{1+x^4}>1-2ax+x^2$ holds for all positive x. (3 points)

11th International Hungarian Mathematics Competition

B. 3586. For what values of the parameter a does the equation log (ax) =2log (x+1) have exactly one root? (4 points)

B. 3587. A truncated right pyramid with a square base is circumscribed about a sphere. Find the range for the ratio of the volume and the surface area of the solid. (4 points)

B. 3588. M is a point in the interior of a given circle. The vertex of a right angle is M and its arms intersect the circle at the points A and B. What is the locus of the midpoint of the line segment AB as the right angle is rotated about the point M? (4 points)

B. 3589. Prove that there are infinitely many odd positive integers n, such that 2ⁿ+n is a composite number. (4 points)

B. 3590. The roots of the equation x³-10x+11=0 are u, v and w. Determine the value of arctan u +arctan v+arctan w. (5 points)

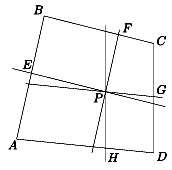
B. 3591. The area of the convex quadrilateral ABCD is T, and P is a point in its interior. The parallel through the point P to the line segment BC intersects the side BA at E, the parallel to the line segment AB intersects the side BC atF, the parallel to AD intersects CD at G, and the parallel to CD intersects AD at the point H. Let t₁ denote the area of the quadrilateral AEPH, and let t₂ denote the area of the quadrilateral PFCG. Prove that $\displaystyle \sqrt{t_1}+\sqrt{t_2}\leq\sqrt{T}$. (5 points)

New advanced problems

Maximum score for each advanced problem (sign "A") is 5 points.

A. 302. Given the unit square ABCD and the point P on the plane, prove that

$\displaystyle 3AP+5CP+\sqrt5(BP+DP)\ge6\sqrt2.$

A. 303. x, y are non-negative numbers, and x³+y⁴$\displaystyle \le$x²+y³. Prove that x³+y³$\displaystyle \le$2.

A. 304. Find all functions R⁺$\displaystyle \mapsto$R⁺, such that

f(x+y)+f(x)^.f(y)=f(xy)+f(x)+f(y)?

Send your solutions to the following address:

or by e-mail to:

solutions@komal.hu

Already signed up?
New to KöMaL?