Exercises and problems in Physics
November 2002

Please read The Conditions of the Problem Solving Competition.

Experimental problem

M. 238. Fill up a vertically standing funnel with water while closing its opening underneath. Then open the hole, and let the water pour out. Measure the position of the water level as a function of time. How will the sinking rate of the water level change? (6 points)

Theoretical problems It is allowed to send solutions for any number of problems, but final scores of students of grades 9-12 are computed from the 5 best score in each month. Final scores of students of grades 1-8 are computed from the 3 best scores in each month.

P. 3571. There is a metal cube, which is empty inside. The length of its edge is 5 mm, and its wall thickness is 1 mm. The density of the metal is 8400 kg/m³. What will happen to the cube if we keep it under water and then release it? (3 points)

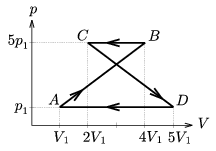
P. 3572. A certain amount of ideal gas is going through a thermal cycle (shown in the figure). What is the amount of work done by the gas in one cycle? (3 points)

P. 3573. What amount of work is needed to shut a door made of solid wood of a mass of 24 kg, so that its edge impacts against its case with a velocity of 5 m/s? (4 points)

P. 3574. How much heat is to be subtracted from 2 kg supercooled water of -5 ^oC, to make ice of it of the same temperature? (4 points)

P. 3575. A dog of mass m is standing on a sledge of mass M. It is capable of jumping off the sledge with a relative velocity of u, and then can run at a velocity of v after the sledge and jump on it again. Neglecting the friction of the sledge on snow-covered horizontal ground, determine what maximum velocity the sledge and the dog can reach in this way and how many times the dog jumps on the sledge in the meantime? (Let M=30 kg, m=10 kg, u=0.5 m/s and v=4 m/s.) (5 points)

P. 3576. We put a solid cylinder on a fixed slope of an angle of \(\displaystyle \alpha\)=30^o. We pull the cylinder using a thread coiled around it in a perpendicular direction to the slope with a force of F=x^.mg. The cylinder rolls down the slope without sliding. a) Determine and plot the static coefficient of friction as a function of x. b) What is the minimum value of x if the surface of the slope is very smooth? c) What is the minimum value of the static coefficient of friction if the centerline of the cylinder moves with an acceleration of 2g? (5 points)

P. 3577. What is the inductivity of a toroid coil with a rectangular cross section? The number of turns in the coil is N, and the radius of the central circle is R. The lengths of the sides of the rectangle are a and b. The sides of length a are parallel with the axis of the toroid. Data: N=1000, R=10 cm, a=6 cm, b=4 cm. (5 points)

P. 3578. The 0.1 mm diameter water droplets of a cloud are charged up to 10 V. The smaller droplets join into bigger droplets of a diameter of 2.7 mm. What will their electric potential be? (4 points)

P. 3579. Ho much faster is a proton than an \(\displaystyle \alpha\)-particle speeded up by the same accelerating voltage? The initial velocities are negligible. (4 points)

P. 3580. In a revolving cylindrical shape gymnasium of a space station `artificial gravitation' the same as the terrestrial g is maintained. When the gymnasium is not in use, they slow it down (out of a false understanding of economy) with constant deceleration to maintain only half of the usual value of gravity. How long does the deceleration take if they don't want the carpets to slip from their places? (The static coefficient of friction between the carpets and the floor is at least 0.1.) To what extent can the deceleration time be reduced if we do not insist on constant deceleration? How much time is needed to achieve complete weightlessness this way? (6 points)

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary

solutions@komal.hu.

Deadline: 11 December 2002