Exercises and problems in Physics
January 2003
Please read The Conditions of the Problem Solving Competition.
 | Experimental problem |
M. 239. Cut out a circular disk of aluminium foil with a radius of R+h, press it on the surface of a cylinder of radius R in a way that detached from the cylinder the foil forms a bowl of height h. Choosing different R values determine with measurements the dependence of the steady falling rate of the bowl on the value of R. Determine the dependence of the form factor of the aerodynamic drag on the R/h ratio.
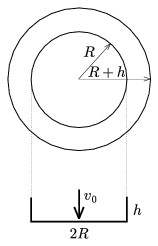
(6 points)
 | Theoretical problemsIt is allowed to send solutions for any number of problems, but final scores of students of grades 9-12 are computed from the 5 best score in each month. Final scores of students of grades 1-8 are computed from the 3 best scores in each month. |
P. 3581. One of the biggest diamonds in the world weighs 44.5 carats and is almost pure carbon. How many carbon atoms are there in this crystal giant?
(3 points)
P. 3582. On an air-cushioned table there are
three equal disks of uniform mass distribution. Two of the disks are
touching each other motionless. The third disk is approaching these,
and its velocity is perpendicular to the line connecting the centers
of the other two. Give the velocity ratios after the perfectly elastic
and frictionless collision as a function of angle 
shown in the
figure.
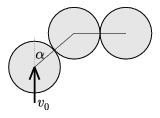
(5 points)
P. 3583. A tube of a radius of R=20 cm is fixed with its axis horizontal. Inside it we slightly remove a solid sphere of radius of r=6 cm from its place of equilibrium and then release it. What will be the periodicity of the resulted motion, if the sphere rolls without sliding. At most what can the amplitude of the motion be, if the static coefficient of friction is \(\displaystyle \mu\)=0.05?
(5 points)
P. 3584. The change of state of a certain amount of helium gas is described with the formula pV3=constant. At the end of the process the absolute temperature of the gas decreases to the fourth of its original value and its internal energy changes by 1800 J. During the process the lowest value of its pressure is 105 Pa. Plot the process in the p-V diagram and indicate the parameters at the end points too.
(4 points)
P. 3585. There is an extensive metal plate
bent at a right angle. We place a small body of mass m and of
electric charge Q in equal d distances from the two
sides of the plate and then release the body. a) At what
acceleration does the body start off? b) What is its
velocity after covering a distance of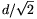 
? (The
gravitational effect is neglected here.)
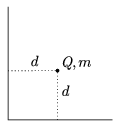
(5 points)
P. 3586. In a space ship there is air of temperature T, pressure p0 and volume V. Suddenly a hole of cross section A appears in the wall of the space ship and the air slowly escapes through it. How long does it take for the pressure to decrease to the half of its original value? (Assuming that the temperature of the air inside doesn't change.)
(5 points)
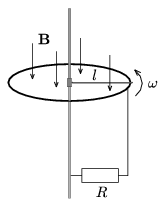
P. 3587. There is a horizontal metal rod
connected to a vertically standing conductor axle so that it can pivot
around the axle. The other end of the rod is resting on a conductor
ring of radius l. The ring and the axle is connected, as shown
in the figure, with an R resistance. (The resistance of
any other conductor and the friction is negligible.) This device is in
a vertical homogeneous magnetic field of magnetic induction
B. How much force is needed at the middle of the rod to ensure
that the rod rotates at a constant angular velocity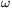 
? The
data: R=0.1 k\(\displaystyle \Omega\), B=0.8 T,
l=0.5 m, \(\displaystyle \omega\)=10 s-1.
(4 points)
P. 3588. There is an electric network of U=230 V effective voltage. We connect to it in cascade a 230 Ohm resistance, an ideal diode and an ammeter, which measures the effective value of the electric current. What does the ammeter show?
(3 points)
P. 3589. On a vertical wall there are circular bells fixed in the grid points of an imaginary quadratic lattice. If we throw 10 mm balls at the wall, averagely every fourth throw sounds a bell. If we throw 30 mm balls, averagely every second throw hits a bell. Assuming that the hits are completely random, determine the lattice spacing and the diameter of the bells.
(4 points)
P. 3590. The alpha decay of the 238U is followed by two beta decay events. What are the proton and the nucleon numbers of the great-grandchild of the 238U? What is the name of this element?
(3 points)
Send your solutions to the following address:
- KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary