Exercises and problems in Informatics May 2003

Please read The Conditions of the Problem Solving Competition.

I. 52. Every natural number N (1\(\displaystyle \le\)N\(\displaystyle \le\)100) can be decomposed as \(\displaystyle N=\sum_{i=1}^kx_i\) with 1\(\displaystyle \le\)k\(\displaystyle \le\)N, the numbers x_i being positive integers for all i, further x_i\(\displaystyle \ge\)x_i+1.

Write a program (i52.pas,...) which reads the value of N, then writes 1000 random decompositions of the number N into the text file i52.ki (repeated decompositions are allowed). Every row of the file should contain only one decomposition, further, terms of any decomposition should be separated by spaces. The decompositions should be random in the sense that each possible outcome should appear with equal probability.

The example shows the first few lines of a file containing possible decompositions of the number N=5.

4 1
1 1 1 1 1
3 2
5
3 2
3 1 1
...

(10 points)

I. 53. A circle of radius Q rolls along counter-clockwise on the circumference of an inner circle of radius R. A point on the rolling circle and with distance A^.Q from its centre is marked (A\(\displaystyle \ge\)0, Q,R>0 are real numbers). The first figure shows a starting position with A=2, R=40, Q=20.

Write a program (i53.pas, ...) which reads the values of A, F, Q and R, then draws the curve traced by the specified point during at most F revolutions.

The examples show other orbits for different parameter values.
(10 points)

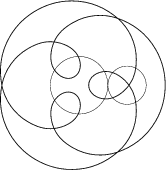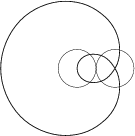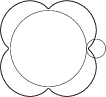A=2, R=30, Q=20	A=2, R=20, Q=20	A=0,8, R=40, Q=10

I. 54. A stable tower of numbered building blocks with various sizes is built in such a way that only a smaller block with larger number can be put onto any other block.

Prepare your sheet (i54.xls) which - using the data of N (1\(\displaystyle \le\)N \(\displaystyle \le\)10) blocks (i.e. the number of the blocks and their sizes in the first two columns) - computes (in the last row) the highest possible stable tower that can be built out of them. (The size of any cube is a positive integer.)

Your sheet should also contain (in the third column) the heights of the highest stable towers with the i^th block (1\(\displaystyle \le\)i \(\displaystyle \le\)10) on the top.

In the example, one should use the 2^nd, 5^th, 6^th and 8^th blocks to build the highest tower.
(10 points)

Send your solutions to the following e-mail address:

infotech@komal.elte.hu.

Deadline: 13 June 2003