 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
I. 67. There are N teams playing a round tournament (2\(\displaystyle \le\)N \(\displaystyle \le\)100, with N even). Write your program (i67.pas, ...) that displays a draw for rounds fulfilling the requirements that every team should play in any round, and should meet with any other team exactly once.
See the example for N=4:
|
(10 points)
I. 68. Any binary tree can be represented as a parenthetical expression. For example, (X) corresponds to a tree with one node, while ((X)X(X)) denotes a tree consisting of the root and its left and right child. See further examples.
| ((X)X) |  |
| (X(X)) |  |
| (((X(X))X)X((X)X((X)X(X)))) | 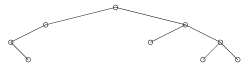 |
Write your program (i68.pas, ...) whose input is a parenthetical expression representing a binary tree (containing at least one node), then displays the tree (see the figures).
I. 69. Prepare a sheet (i69.xls) so that one can write both into its first and second rows a strictly monotone increasing integer sequence having at most 100 terms. Both sequences will terminate in an empty cell. After the sequences have been entered, a merged sequence should appear in the third row, that is the strictly monotone increasing sequence consisting of the terms of the original ones, but with terms occurring in both of them listed only once. (Solutions using macros are awarded at most half of the score.)
|
(10 points)
