Exercises and problems in Physics
February 2004
Please read The Conditions of the Problem Solving Competition.
 | Experimental problem |
M. 249. We are dropping balls of smaller density than that of water into water in a big sized transparent vessel. How does penetrating depth H depend on dropping height h and radius r of the ball?
(6 points)
 | Theoretical problemsIt is allowed to send solutions for any number of problems, but final scores of students of grades 9-12 are computed from the 5 best score in each month. Final scores of students of grades 1-8 are computed from the 3 best scores in each month. |
P. 3682. The intercity express train from Pécs to Budapest departs exactly at 6:55. An observer who is standing on the platform at the middle carriage sees on his watch that it is 6:55 when the last carriage but one is beginning to pass him. This one passes him in 8 seconds and the last one in 6 seconds. Provided that the train accelerates uniformly, how many seconds is the observer's watch late?
(4 points)
P. 3683. Estimate the air pressure difference between the floor and the ceiling of a room.
(3 points)
P. 3684. There are two identical voltmeters with a measuring limit of 10 V each. How can we measure the electromotive force of a 12 V car battery with them? What do the two instruments show?
(3 points)
P. 3685. A square carpet of a mass of 20 kg is dragged from one room into another as shown in the figure. The width of the corridor and the carpet is the same, 2 m. The friction coefficient is 0.1 in the first room and 0.2 in the other and in the corridor it changes evenly from 0.1 to 0.2. The carpet presses the floor uniformly. What is the amount of work that must be done to drag the carpet from the first room to the other?
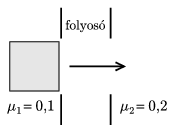
(4 points)
P. 3686. Falling objects in air reach a constant velocity in more or less time. A table-tennis ball of a mass of 4 g, for example, is falling with a velocity of 15 m/s. a) What is the velocity of a falling metal ball of the same size and of a mass of 256 g? b) If the table-tennis and the metal ball is connected with a long line what is their common falling velocity? (The aerodynamic drag is proportional to the square of the velocity.)
(4 points)
P. 3687. At the top of a slope of angle \(\displaystyle \alpha\) there is a water tank in which the water level is at height H. In the side of the tank at height h there is a small hole where a water jet squirts horizontally from the tank. At what value h, does the water jet impact onto the slope furthest from the bottom of the tank, and what is this distance?
(5 points)
P. 3688. An alternating-current generator supplies 120 V effective voltage with a frequency of 60 Hz. When switch K (shown in the figure) is disconnected, the current flowing through the generator leads by 20o ahead of the voltage on the generator. In state 1 of the switch the current follows the voltage by 10o. In state 2 of the switch the effective value of the current is 2.0 A. Determine the values of R, L and C.
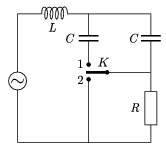
(4 points)
P. 3689. A light source is placed at a 30 cm distance from a convergent lens of focal length of 20 cm on its optical axis. A plane mirror is placed on the other side of the lens perpendicular to the optical axis. How far is the mirror to be placed to get a real image between the light source and the lens?
(5 points)
P. 3690. A car is approaching from a great distance. Its two headlights, which are at a 120 cm distance from each other, can be considered a single point source. How far is the car when even a man of the best eyesight cannot see whether there are one or two sources of light? (Take the diameter of a wide open pupil as 5 mm and the effective wavelength of the light as 550 nm.)
(5 points)
P. 3691. Under what conditions does the energy of a photon increase in an elastic collision with an electron? (Let us assume that the collision takes place along a single line.)
(5 points)
Send your solutions to the following address:
- KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary
